| << Chapter < Page | Chapter >> Page > |
Funksies van die vorm is bekend as eksponensiële funksies. Die algemene vorm van ‘n funksie van hierdie tipe word gewys in [link] .
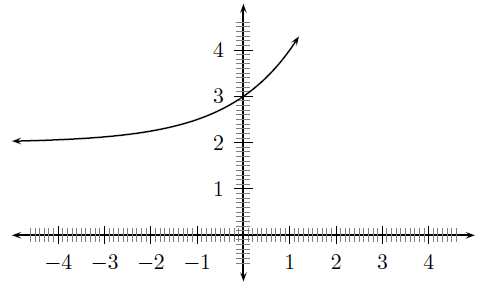
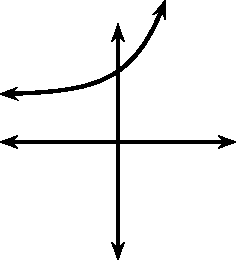
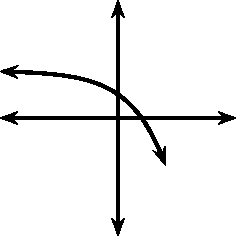
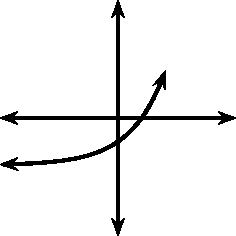
Jy sou gevind het dat die waarde van bepaal die vorm van die grafiek, dit wil sê: “Curves Upwards” – “CU” ( ) of “Curves Downwards” – “CD” ( ).
Jy sou ook gevind het die waarde van bepaal die posisie van die -afsnit.
Hierdie verskillende eienskappe word opgesom in [link] .
 |
 | |
 |
 |
Vir , is die funksie gedefinieer vir alle reële waardes van . Dus, die definisieversameling is .
Die waardeversameling van word bepaal deur die teken van .
As dan:
Dus, as , dan is die waardeversameling .
As dan:
Dus, as , dan is die waardeversameling .
Byvoorbeeld, die definisieversameling van is . Vir die waardeversameling,
Dus is die waardeversameling .
Vir funksies van die vorm, , word die afsnitte met die en -as bereken deur te stel vir die -afsnit en deur te stel vir die -afsnit.
Die -afsnit word as volg bereken:
Byvoorbeeld, die -afsnit van word gegee deur te stel, om dan te kry:
Die -afsnitte word bereken deur te stel, soos volg:
Dit het net ‘n rëele oplossing as een van beide of . Anders, het die grafiek van die vorm geen -afsnitte.
Byvoorbeeld, die -afsnit van word gegee deur te stel:
en dit het geen rëele oplossing nie. Dus, die grafiek van het geen -afsnitte nie.
Daar is een asimptoot vir funksies van die vorm . Die asimptoot kan bepaal word deur die analise van die waardeversameling.
Ons het gesien dat die terrein bepaal word deur die waarde van q. As , dan is die terrein .
Dit wys dat die funksiewaarde neig na die waarde van q as . Dus die horisontale asimptoot lê by .
Om grafieke te skets van funksies van die vorm, , moet ons vier eienskappe bereken:
Byvoorbeeld, skets die grafiek van . Merk die afsnitte.
Ons het die definisieversameling bepaal om te wees en die waardeversameling om te wees.

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 10) [caps]' conversation and receive update notifications?