| << Chapter < Page | Chapter >> Page > |
Het jy geweet?
| is ’n egte breuk. Die teller is kleiner as die noemer. | |
| is ’n onegte breuk. Die teller is groter as die noemer. | |
| 1 | is ’n gemengde getal . ’n Gemengde getal is altyd groter as 1 en bestaan uit ’n heelgetal (1) plus ’n breuk ( ). |
1. Kan jy nog onthou hoe ons breuke bymekaar tel? Kom ons kyk. Werk saam met ’n maat. Maak beurte om die antwoorde te sê. Kies enige twee breukdele en tel hulle bymekaar. Gee jou antwoord eers as ’n onegte breuk en dan as ’n gemengde getal.
Vra jul opvoeder se hulp as julle twyfel.
1.1
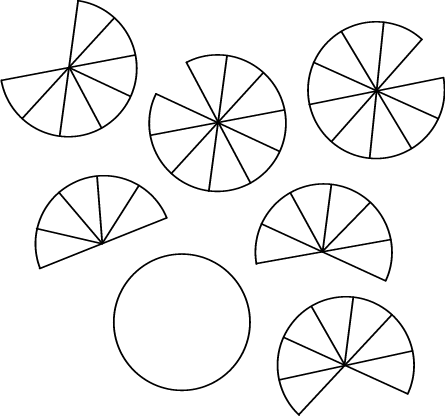 |
1.2
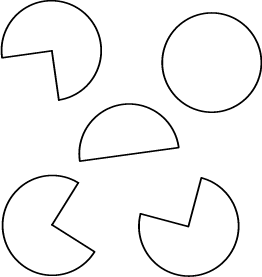 |
6 tot by
1. Kyk goed na die volgende vrae en voltooi dit so netjies soos jy kan.
EKWIVALENTE BREUKE
Kleur van die figuur blou in:
1.3 Kleur van die figuur geel in
| 1.6 Voltooi: | |
| 1 | |
| 2 | = |
| .... | |
| 4 | = |
| 4 | |
| .... | = |
| .... | |
| 16 |
Het jy geweet?
Ons noem breuke wat ewe groot is, ekwivalente breuke. Die woord ekwivalent beteken gelykwaardig. Dus is die breuke gelyk aan mekaar.
Onthou jy nog?
| 1 eenheid | |||||||||||
2. Die volgende oefening sal jou voorberei vir die optelling en aftrekking van breuke. Gebruik jou kennis van ekwivalente breuke en beantwoord die volgende. Waar jy twyfel, kan jy die diagram hierbo gebruik.
2.1 2.6
2.2 2.7
2.3 2.8
2.4 2.9
2.5 2.10
3. As jy die reëls waarna ons nou net gekyk en wat ons bespreek het, korrek kan toepas, sal jy nooit sukkel om breuke op te tel en af te trek nie. Gebruik die bostaande reëls en voltooi:
3.1 3.2
3.3 3.4
3.5 3.6
1. Jy weet nou al hoe belangrik dit is om vinnig ‘n antwoord te kan bereken. Skryf net die antwoorde neer en dan kyk ons hoe goed jy in hierdie hoofrekentoets vaar.
| 1.1 4 × 7 = | 1.11 23 + 49 = |
| 1.2 8 × 5 = | 1.12 104 – 29 = |
| 1.3 × 6 = 36 | 1.13 = |
| 1.4 9 × = 45 | 1.14 = |
| 1.5 28 ÷ 7 = | 1.15 = |
| 1.6 35 ÷ 5 = | 1.16 = |
| 1.7 ÷ 9 = 6 | 1.17 = |
| 1.8 56 ÷ = 7 | 1.18 = |
| 1.9 560 ÷ = 70 | 1.19 = |
| 1.10 13 + 29 = | 1.20 = |
| Leeruitkomstes(LUs) |
| LU 1 |
| Getalle, Verwerkings en VerwantskappeDie leerder is in staat om getalle en die verwantskappe daarvan te herken, te beskryf en voor te stel, en om tydens probleemoplossing bevoeg en met selfvertroue te tel, te skat, te bereken en te kontroleer. |
| Assesseringstandaarde(ASe) |
| Dit is duidelik wanneer die leerder: |
| 1.1 aan- en terugtel in breuke-intervalle; |
| 1.2 verskeie maniere om getalle neer te skryf deur die geskiedenis heen in verskillende kulture (insluitend plaaslik) beskryf en illustreer; |
1.3 die volgende getalle herken en voorstel, sodat dit beskryf en vergelyk kan word:
|
1.5 ekwivalente vorms van die bogenoemde getalle herken en gebruik, insluitend:
|
1.6 probleme in kontekste oplos, insluitend kontekste wat gebruik kan word om ‘n bewustheid van ander leerareas, asook van menseregte-, sosiale, ekonomiese en omgewingskwessies, te bevorder, soos:
|
1.8 deur geskikte bewerkings skat en bereken vir die oplossing van probleme in verband met die volgende te kies en gebruik:
|
| 1.9 hoofberekings uitvoer wat die volgende behels:1.9.1 optelling en aftrekking;1.9.2 vermenigvuldiging van heelgetalle tot minstens 10 x 10; |
1.10 ‘n verskeidenheid tegnieke gebruik om sowel skriftelike as hoofberekeninge met heelgetalle te doen, insluitend:
|
| 1.11 ‘n verskeidenheid strategieë gebruik om oplossings te kontroleer en die redelikheid van oplossings te beoordeel. |
| LU 2 |
| Patrone, funksies en algebraDie leerder is in staat om patrone en verwantskappe te herken, te beskryf en voor te stel en probleme op te los deur algebraïese taal en vaardighede te gebruik. |
| Dit is duidelik wanneer die leerder: |
| 2.2 verwantskappe of reëls wat waargeneem is in eie woorde beskryf; |
| 2.4 getalsinne skryf om ‘n probleemsituasie te beskryf, insluitend probleme binne kontekste wat gebruik kan word om ‘n bewustheid van menseregte-, sosiale, ekonomiese, kulturele en omgewingsake te bevorder; |
2.6 bepaal, deur bespreking en vergelyking, die ekwivalensie van verskillende beskrywings van dieselfde verwantskap of reël wat soos volg voorgestel word:
|
| LU 5 |
| DatahanteringDie leerder is in staat om data te versamel, op te som, voor te stel en krities te ontleed om gevolgtrekkings en voorspellings te maak en om toevallige variasies te interpreteer en te bepaal. |
| Dit is duidelik wanneer die leerder: |
| 5.3 data organiseer en aanteken deur tellings en tabelle te gebruik; |
5.5 ‘n verskeidenheid grafieke teken om data (ongegroepeer) voor te stel en te interpreteer, insluitend:
|
AKTIWITEIT 1
1.1 Gelyke deel van ‘n hele
1.2 Teller
1.3
1.5 Kleiner
1.6 Noemer
1.7 Ekwivalente
1.8 Groter
1.9 Sê met hoeveel gelyke dele ek werk / ingekleur is
1.10 Deel die teller en noemer deur dieselfde getal
2. 2.1 b en c
2.4 Nie ewe groot dele nie
2.5 (i)
(ii) /
(iii) /
(iv)
(v)
(vi)
(vii) /
(viii) /
(ix)
(x)
(xi)
AKTIWITEIT 2
1.
| B | 8 | 1 | 7 | |||
| C | 6 | 1 | 5 | |||
| D | 8 | 1 | 7 | |||
| E | 3 | 1 | 2 | |||
| F | 12 | 6 | / | 6 | / | |
| G | 16 | 8 | / | 8 | / | |
| H | 16 | 4 | / | 12 | / | |
| I | 8 | 2 | / | 6 | / | |
| J | 12 | 6 | / | 6 | / | |
| K | 8 | 2 | / | 6 | / |
AKTIWITEIT 5
1. 1.1 28 1.11 72
1.8 8 1.18 3
1.9 8 1.19 5 / 5
1.10 42 1.20 5

Notification Switch
Would you like to follow the 'Wiskunde graad 5' conversation and receive update notifications?