1. Home
  2. College physics (engineering
  3. Fluid statics
  4. Variation of pressure with depth

1.3 Variation of pressure with depth in a fluid  (Page 6/4)

<< Chapter < Page
  College physics (engineering     Page 1 / 4
Chapter >> Page >
  • Define pressure in terms of weight.
  • Explain the variation of pressure with depth in a fluid.
  • Calculate density given pressure and altitude.

If your ears have ever popped on a plane flight or ached during a deep dive in a swimming pool, you have experienced the effect of depth on pressure in a fluid. At the Earth’s surface, the air pressure exerted on you is a result of the weight of air above you. This pressure is reduced as you climb up in altitude and the weight of air above you decreases. Under water, the pressure exerted on you increases with increasing depth. In this case, the pressure being exerted upon you is a result of both the weight of water above you and that of the atmosphere above you. You may notice an air pressure change on an elevator ride that transports you many stories, but you need only dive a meter or so below the surface of a pool to feel a pressure increase. The difference is that water is much denser than air, about 775 times as dense.

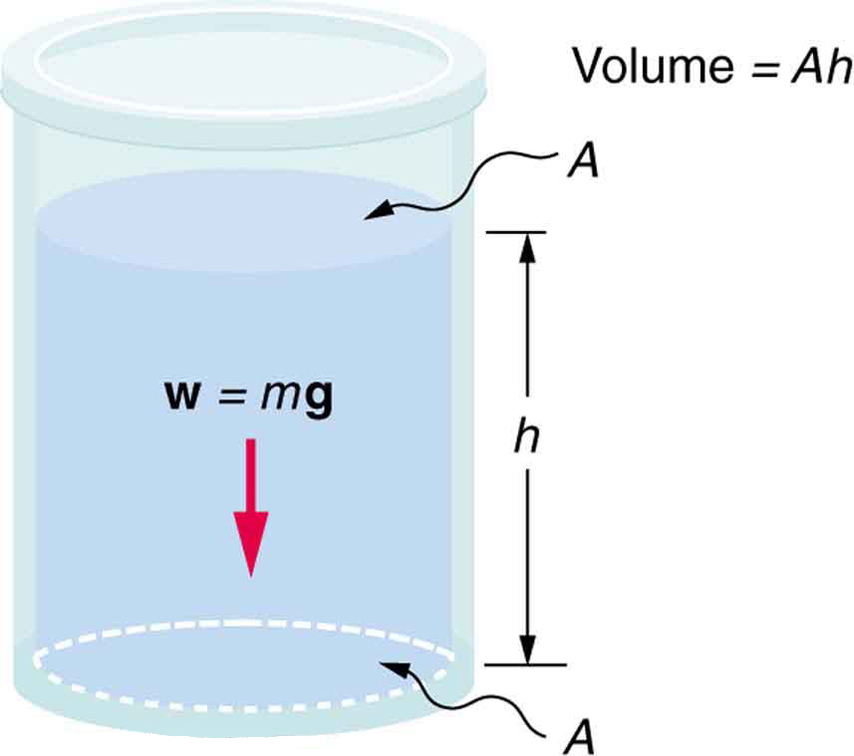
Consider the container in [link] . Its bottom supports the weight of the fluid in it. Let us calculate the pressure exerted on the bottom by the weight of the fluid. That pressure    is the weight of the fluid mg size 12{ ital "mg"} {} divided by the area A size 12{A} {} supporting it (the area of the bottom of the container):

P = mg A . size 12{P= { { ital "mg"} over {A} } } {}

We can find the mass of the fluid from its volume and density:

m = ρV . size 12{m=ρV} {}

The volume of the fluid V size 12{V} {} is related to the dimensions of the container. It is

V = Ah , size 12{V= ital "Ah"} {}

where A size 12{A} {} is the cross-sectional area and h size 12{h} {} is the depth. Combining the last two equations gives

m = ρ Ah . size 12{m=ρ ital "Ah"} {}

If we enter this into the expression for pressure, we obtain

P = ρ Ah g A . size 12{P= { { left (ρ ital "Ah" right )g} over {A} } } {}

The area cancels, and rearranging the variables yields

P = hρg . size 12{P=hρg} {}

This value is the pressure due to the weight of a fluid . The equation has general validity beyond the special conditions under which it is derived here. Even if the container were not there, the surrounding fluid would still exert this pressure, keeping the fluid static. Thus the equation P = hρg size 12{P=hρg} {} represents the pressure due to the weight of any fluid of average density ρ size 12{ρ} {} at any depth h size 12{h} {} below its surface. For liquids, which are nearly incompressible, this equation holds to great depths. For gases, which are quite compressible, one can apply this equation as long as the density changes are small over the depth considered. [link] illustrates this situation.

A container with fluid filled to a depth h. The fluid’s weight w equal to m times g is shown by an arrow pointing downward. A denotes the area of the fluid at the bottom of the container and as well as on the surface.
The bottom of this container supports the entire weight of the fluid in it. The vertical sides cannot exert an upward force on the fluid (since it cannot withstand a shearing force), and so the bottom must support it all.

Calculating the average pressure and force exerted: what force must a dam withstand?

In [link] , we calculated the mass of water in a large reservoir. We will now consider the pressure and force acting on the dam retaining water. (See [link] .) The dam is 500 m wide, and the water is 80.0 m deep at the dam. (a) What is the average pressure on the dam due to the water? (b) Calculate the force exerted against the dam and compare it with the weight of water in the dam (previously found to be 1.96 × 10 13 N ).

Strategy for (a)

The average pressure P ¯ due to the weight of the water is the pressure at the average depth h ¯ of 40.0 m, since pressure increases linearly with depth.

Solution for (a)

The average pressure due to the weight of a fluid is

P ¯ = h ¯ ρg . size 12{P=hρg} {}

Entering the density of water from [link] and taking h ¯ size 12{h} {} to be the average depth of 40.0 m, we obtain

P ¯ = ( 40.0 m ) 10 3 kg m 3 9.80 m s 2 = 3.92 × 10 5 N m 2 = 392 kPa.

Strategy for (b)

The force exerted on the dam by the water is the average pressure times the area of contact:

F = P ¯ A . size 12{F= {overline {P}} A} {}

Solution for (b)

We have already found the value for P ¯ size 12{ { bar {P}}} {} . The area of the dam is A = 80.0 m × 500 m = 4.00 × 10 4 m 2 size 12{A="80" "." 0`m times "500"`m=4 "." "00" times "10" rSup { size 8{4} } `m rSup { size 8{2} } } {} , so that

F = ( 3.92 × 10 5 N/m 2 ) ( 4.00 × 10 4 m 2 ) = 1.57 × 10 10 N. alignl { stack { size 12{F= \( 3 "." "92" times "10" rSup { size 8{5} } `"N/m" rSup { size 8{2} } \) \( 4 "." "00" times "10" rSup { size 8{4} } `m rSup { size 8{2} } \) } {} #" "=1 "." "57" times "10" rSup { size 8{"10"} } `N "." {} } } {}

Discussion

Although this force seems large, it is small compared with the 1.96 × 10 13 N size 12{1 "." "96" times "10" rSup { size 8{"13"} } `N} {} weight of the water in the reservoir—in fact, it is only 0.0800% of the weight. Note that the pressure found in part (a) is completely independent of the width and length of the lake—it depends only on its average depth at the dam. Thus the force depends only on the water’s average depth and the dimensions of the dam, not on the horizontal extent of the reservoir. In the diagram, the thickness of the dam increases with depth to balance the increasing force due to the increasing pressure.epth to balance the increasing force due to the increasing pressure.

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College physics (engineering physics 2, tuas). OpenStax CNX. May 08, 2014 Download for free at http://legacy.cnx.org/content/col11649/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College physics (engineering physics 2, tuas)' conversation and receive update notifications?

Ask