| << Chapter < Page | Chapter >> Page > |
For the following exercises, find the exact value of each expression.
1
2
For the following exercises, use reference angles to evaluate the expression.
−1
−2
2
−2
−1
If and is in quadrant II, find
If and is in quadrant III, find
If
If and find and
If and find and
If
If what is the
If what is the
If what is the
3.1
If what is the
If what is the
1.4
If what is the
For the following exercises, use the angle in the unit circle to find the value of the each of the six trigonometric functions.
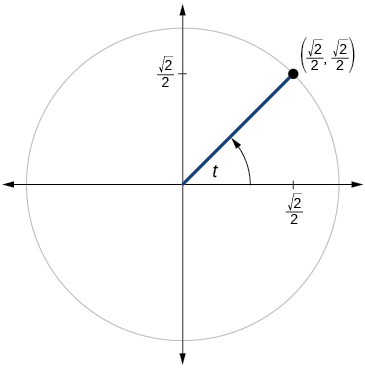
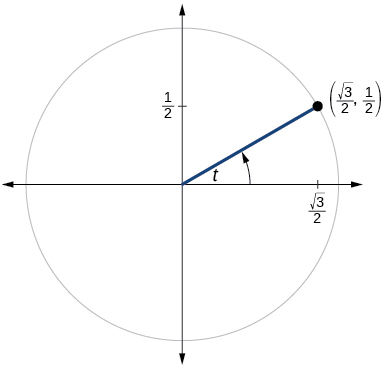
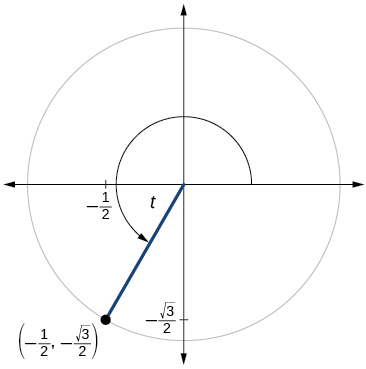
For the following exercises, use a graphing calculator to evaluate.
–0.228
–2.414
1.414
1.540
1.556
For the following exercises, use identities to evaluate the expression.
If and find
If and find
If and find
If and find
Determine whether the function is even, odd, or neither.
Determine whether the function is even, odd, or neither.
even
Determine whether the function is even, odd, or neither.
Determine whether the function is even, odd, or neither.
even
For the following exercises, use identities to simplify the expression.
The amount of sunlight in a certain city can be modeled by the function where represents the hours of sunlight, and is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the 42 nd day of the year. State the period of the function.
The amount of sunlight in a certain city can be modeled by the function where represents the hours of sunlight, and is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the 267 th day of the year. State the period of the function.
13.77 hours, period:
The equation models the blood pressure, where represents time in seconds. (a) Find the blood pressure after 15 seconds. (b) What are the maximum and minimum blood pressures?
The height of a piston, in inches, can be modeled by the equation where represents the crank angle. Find the height of the piston when the crank angle is
7.73 inches
The height of a piston, in inches, can be modeled by the equation where represents the crank angle. Find the height of the piston when the crank angle is

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?