| << Chapter < Page | Chapter >> Page > |
0
−1
For the following exercises, state the reference angle for the given angle.
For the following exercises, find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not one of the angles on the unit circle, use a calculator and round to three decimal places.
Quadrant IV,
Quadrant II,
Quadrant II,
Quadrant II,
Quadrant III,
Quadrant II,
Quadrant II,
Quadrant IV,
For the following exercises, find the requested value.
If and is in the 4 th quadrant, find
If and is in the 1 st quadrant, find
If and is in the 2 nd quadrant, find
If and is in the 3 rd quadrant, find
Find the coordinates of the point on a circle with radius 15 corresponding to an angle of
Find the coordinates of the point on a circle with radius 20 corresponding to an angle of
Find the coordinates of the point on a circle with radius 8 corresponding to an angle of
Find the coordinates of the point on a circle with radius 16 corresponding to an angle of
State the domain of the sine and cosine functions.
State the range of the sine and cosine functions.
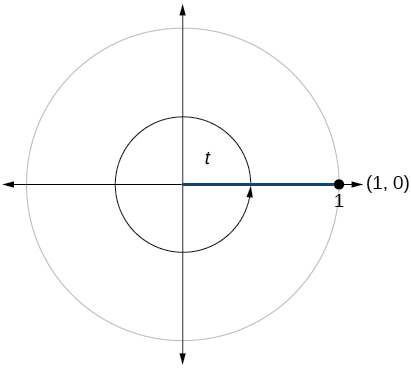
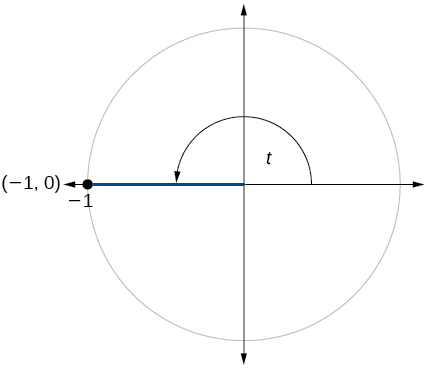
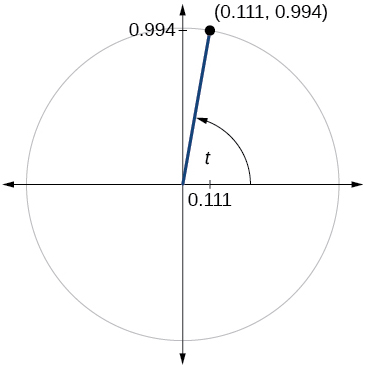
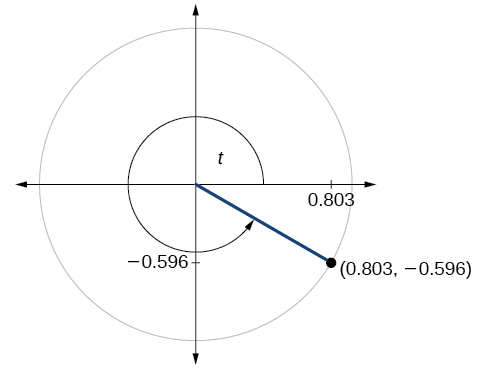
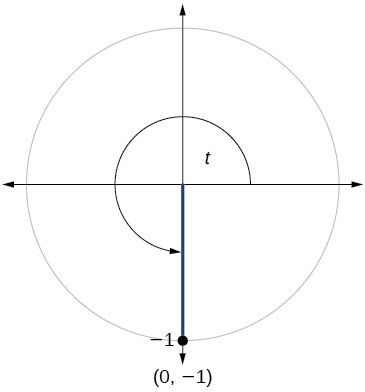
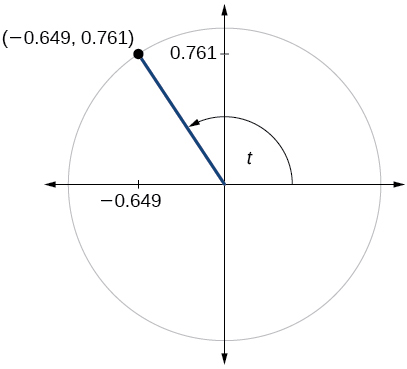
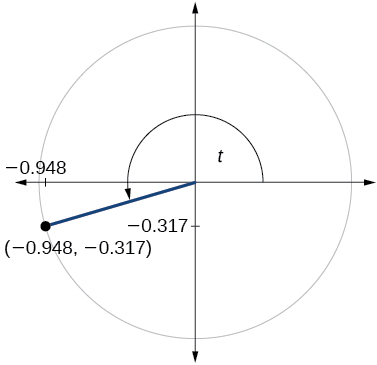
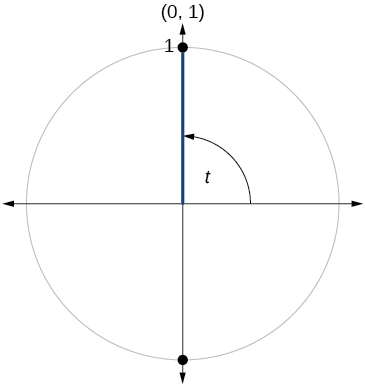
For the following exercises, use the given point on the unit circle to find the value of the sine and cosine of
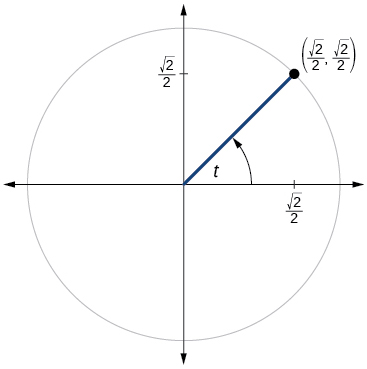
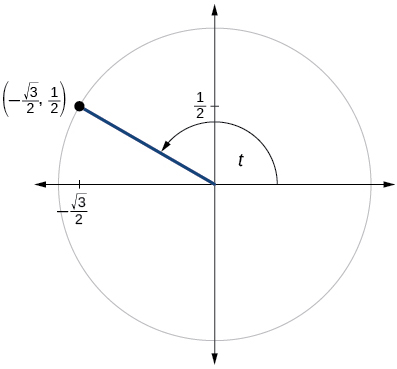
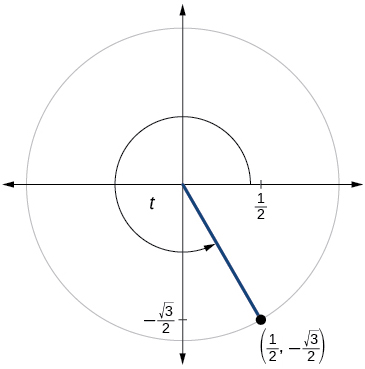
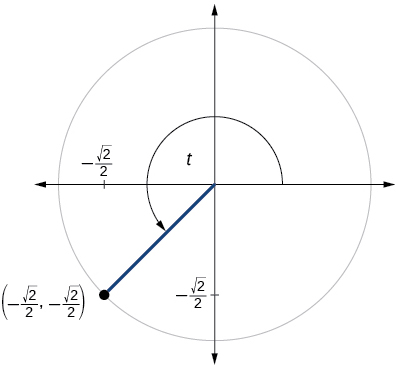
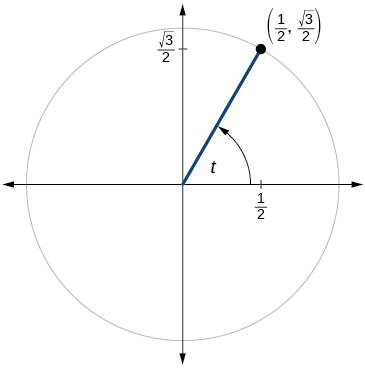
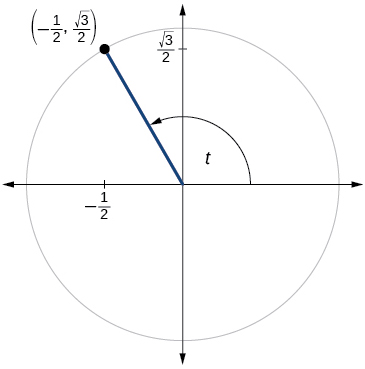
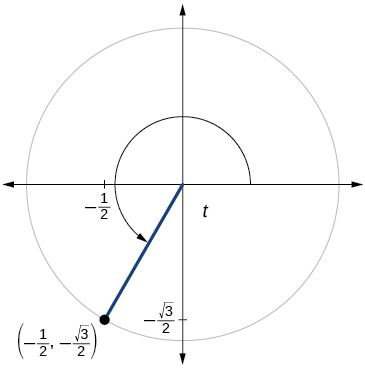
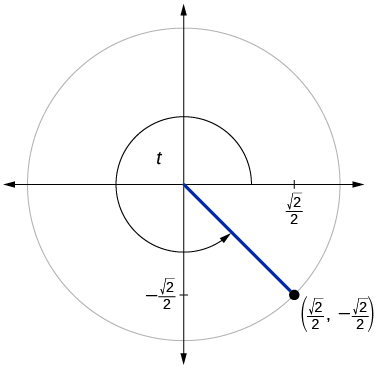
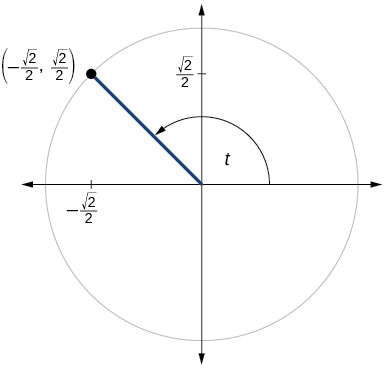
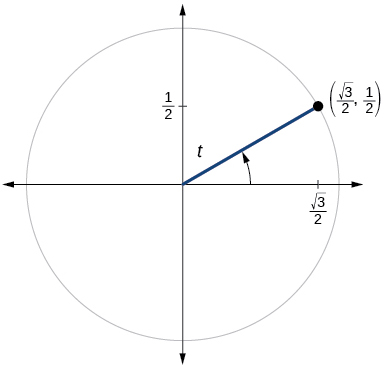
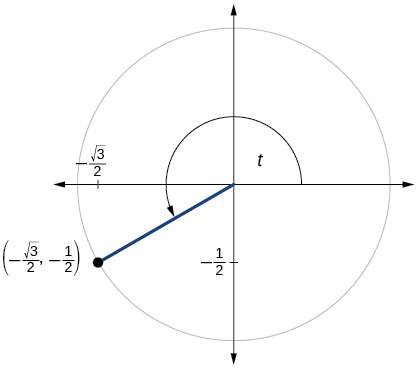
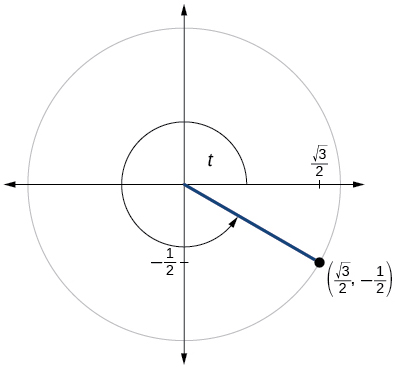
For the following exercises, use a graphing calculator to evaluate.
−0.1736
0.9511
−0.7071
−0.1392
−0.7660
0
For the following exercises, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point that is, on the due north position. Assume the carousel revolves counter clockwise.
What are the coordinates of the child after 45 seconds?
What are the coordinates of the child after 90 seconds?
What is the coordinates of the child after 125 seconds?
When will the child have coordinates if the ride lasts 6 minutes? (There are multiple answers.)
37.5 seconds, 97.5 seconds, 157.5 seconds, 217.5 seconds, 277.5 seconds, 337.5 seconds
When will the child have coordinates if the ride last 6 minutes?

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?