| << Chapter < Page | Chapter >> Page > |
1) Here is a challenging problem for those who know a little calculus. The Newton-Raphson method can be used to find the roots of any equation y(x) = 0.
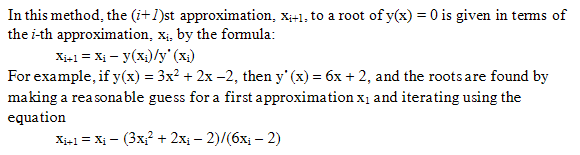
2) a. See the definition of determinant of a matrix as below.

Using this information, write and test two functions, named det2() and det3(). The det2() function should accept the four coefficients of a 2 X 2 matrix and return its determinant. The det3() function should accept the nine coefficients of a 3 X 3 matrix and return its determinant by calling det2() to calculate the required 2 X 2 determinants.
b. Write and run a C++ program that accepts the nine coefficients of a 3 X 3 matrix in one main() function, passes these coefficients to det3() to calculate its determinant and then displays the calculated determinant.
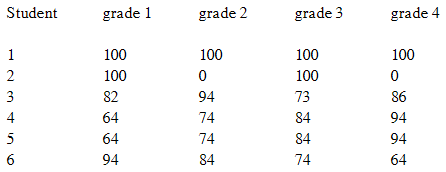
3) Your professor has asked you to write a C++ program that can be used to determine grades at the end of the semester. For each student, who is identified by an integer number between 1 and 60, four examination grades must be kept. Additionally, two final grade averages must be computed. The first grade average is simply the average of all four grades. The second grade average is computed by weighting the four grades as follows: the first grade gets a weight of 0.2, the second grade gets a weight of 0.3,the third grade a weight of 0.3 and the fourth grade a weight of 0.2; that is, the final grade is computed as:
0.2* grade1 + 0.3*grade2 + 0.3*grade3 + 0.2*grade4
Using this information, you are to construct a 60 X 6 two-dimensional array, in which the the first four columns for the grades, and the last two columns for the computed final grades. The output of the program should be a display of the data in the completed array.
For test purposes, the professor has provided the following data:
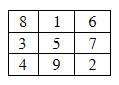
4) A magic square is an n X n matrix in which each of the integer values from 1 to n*n appears exactly once and all column sums, row sums and diagonal sums are equal. For example, the following is a 3 X 3 magic square in which each row, each column, and each diagonal adds up to 15.

Notification Switch
Would you like to follow the 'Programming fundamentals in c++' conversation and receive update notifications?