| << Chapter < Page | Chapter >> Page > |
Young’s double slit experiment breaks a single light beam into two sources. Would the same pattern be obtained for two independent sources of light, such as the headlights of a distant car? Explain.
Suppose you use the same double slit to perform Young’s double slit experiment in air and then repeat the experiment in water. Do the angles to the same parts of the interference pattern get larger or smaller? Does the color of the light change? Explain.
Is it possible to create a situation in which there is only destructive interference? Explain.
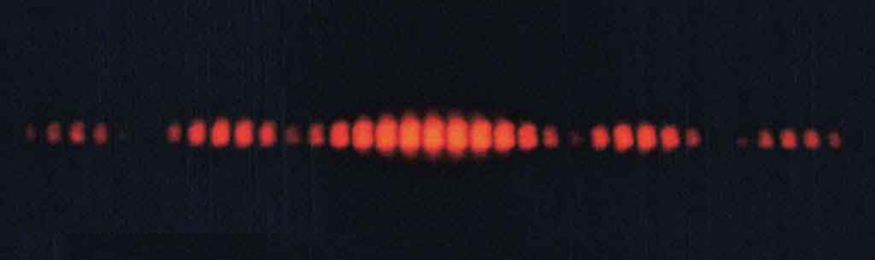
[link] shows the central part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single slit and double slit interference. Note that the bright spots are evenly spaced. Is this a double slit or single slit characteristic? Note that some of the bright spots are dim on either side of the center. Is this a single slit or double slit characteristic? Which is smaller, the slit width or the separation between slits? Explain your responses.
At what angle is the first-order maximum for 450-nm wavelength blue light falling on double slits separated by 0.0500 mm?
Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double slits separated by 0.100 mm.
What is the separation between two slits for which 610-nm orange light has its first maximum at an angle of ?
Find the distance between two slits that produces the first minimum for 410-nm violet light at an angle of .
Calculate the wavelength of light that has its third minimum at an angle of when falling on double slits separated by . Explicitly, show how you follow the steps in Problem-Solving Strategies for Wave Optics .
600 nm
What is the wavelength of light falling on double slits separated by if the third-order maximum is at an angle of ?
At what angle is the fourth-order maximum for the situation in [link] ?
What is the highest-order maximum for 400-nm light falling on double slits separated by ?
Find the largest wavelength of light falling on double slits separated by for which there is a first-order maximum. Is this in the visible part of the spectrum?
1200 nm (not visible)
What is the smallest separation between two slits that will produce a second-order maximum for 720-nm red light?
(a) What is the smallest separation between two slits that will produce a second-order maximum for any visible light? (b) For all visible light?
(a) 760 nm
(b) 1520 nm
(a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of , at what angle is the second-order maximum? (b) What is the angle of the first minimum? (c) What is the highest-order maximum possible here?
[link] shows a double slit located a distance from a screen, with the distance from the center of the screen given by . When the distance between the slits is relatively large, there will be numerous bright spots, called fringes. Show that, for small angles (where , with in radians), the distance between fringes is given by .
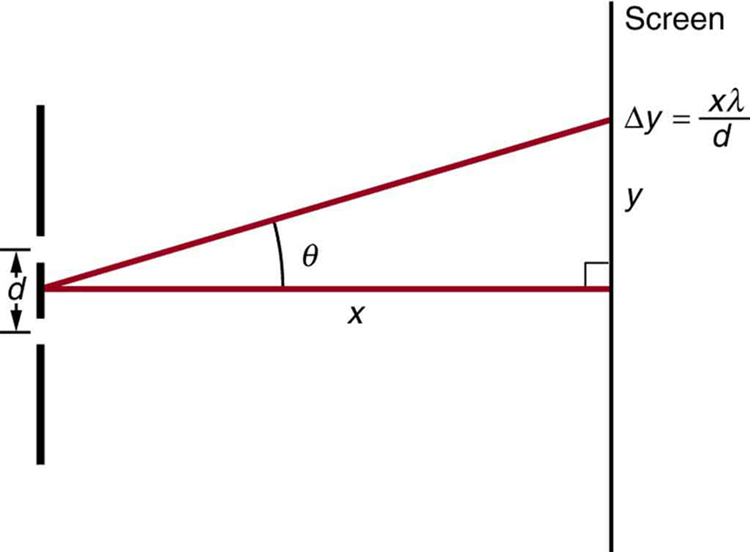
For small angles .
For two adjacent fringes we have,
and
Subtracting these equations gives
Using the result of the problem above, calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen as in [link] .
Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm (see [link] ).
450 nm

Notification Switch
Would you like to follow the 'General physics ii phy2202ca' conversation and receive update notifications?