1.12 Young’s double slit experiment  (Page 2/9)

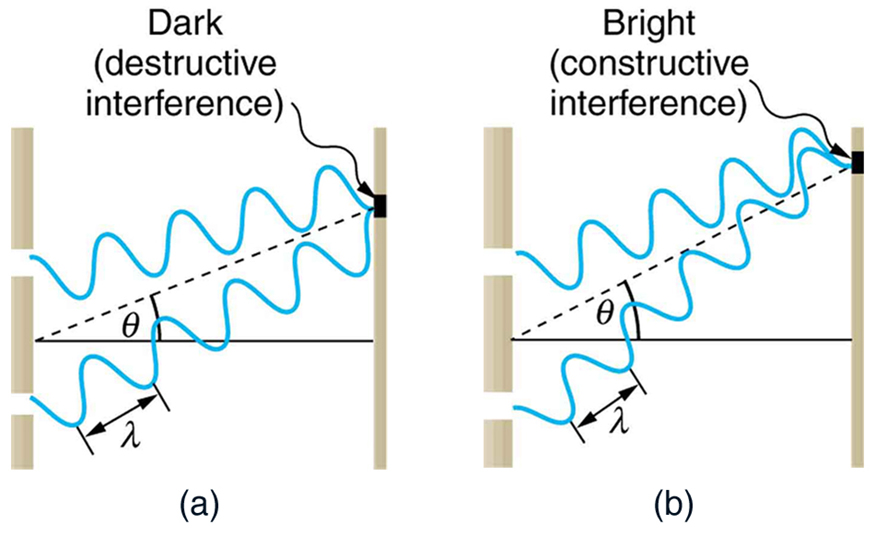
To understand the double slit interference pattern, we consider how two waves travel from the slits to the screen, as illustrated in [link] . Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively as shown in [link] (a). If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively as shown in [link] (b). More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths [ $(1/2)\lambda$ , $(3/2)\lambda$ , $(5/2)\lambda$ , etc.], then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ( $\lambda$ , $2\lambda$ , $3\lambda$ , etc.), then constructive interference occurs.

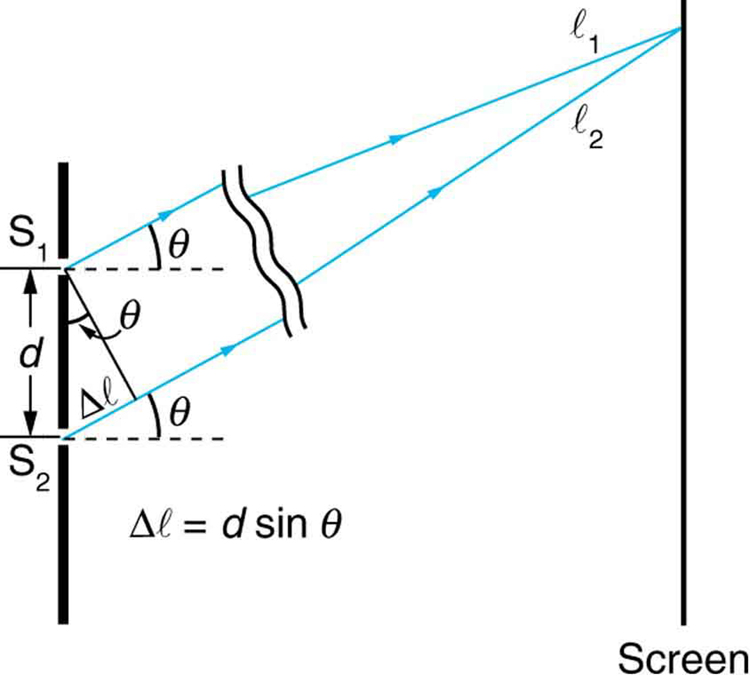
[link] shows how to determine the path length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle $\theta$ between the path and a line from the slits to the screen (see the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be $d\text{sin}\theta$ , where $d$ is the distance between the slits. To obtain constructive interference for a double slit    , the path length difference must be an integral multiple of the wavelength, or

Similarly, to obtain destructive interference for a double slit    , the path length difference must be a half-integral multiple of the wavelength, or

where $\lambda$ is the wavelength of the light, $d$ is the distance between slits, and $\theta$ is the angle from the original direction of the beam as discussed above. We call $m$ the order    of the interference. For example, $m=4$ is fourth-order interference.

The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the light spreads out horizontally on either side of the incident beam into a pattern called interference fringes, illustrated in [link] . The intensity of the bright fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation