| << Chapter < Page | Chapter >> Page > |
1.1 7
1.2 4
1.3 2
1.4 7
1.5 4
2.1 432; 214; 1 346; 1 020; 8 421; 6 045
2.2 512; 294; 1 426; 1 100; 6 125
2.3 1 482; 1 264; 2 396; 2 070; 9 471; 7 095
3.
4.
4.1 26
4.2 66
4.3 34
4.4 44
4.5 94
4.6 49
4.7 49
4.8 351
4.9 368
4.10 9 984
4.11 32
4.12 48
4.13 48
4.14 6
4.15 24
4.16 96
4.17 132
4.18 7
4.19 15
4.20 44
5. 33 000; 43 000; 53 000; 63 000; 73 000; 83 000; 93 000; 103 000;
113 000; 123 000; 133 000
Leaner Section
1. In Mathematics it is important to count "visually". To be able to do this correctly, you must look carefully at the given figure. You must also read the questions carefully and with insight, because if you do not understand them, you will not count correctly! Let us start immediately with a challenge. Work with a friend and count:
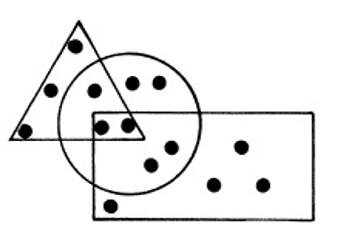
1.1 How many dots are there in the circle? _______________________________
1.2 How many dots are there in the circle, and in the rectangle as well?
_____________________________________________________________________
1.3 How many dots are there in the circle, and in the rectangle and the triangle as well? ________________________________________________________________
1.4 How many dots are outside the circle? _______________________________
1.5 How many dots are in the rectangle, but not in the circle or the triangle? _____________________________________________________________________
2. In the previous activity you counted with small numbers. Let us now use greater numbers. It is important that you know the value of each digit (as we did in the previous Learning Unit) before you start adding. This will help you calculate the answers correctly. See whether you or your friend can say the correct answer first. If you are not sure, check the answer with a calculator.
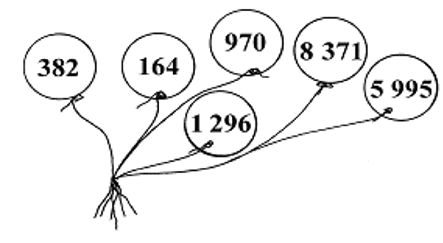
2.1 Add 50 to each balloon’s number.
2.2 Add 130 to each balloon’s number.
2.3 Add 100 to each balloon’s number.
3. Now see whether you can do the following!
Use each of the numbers 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; 11 and 12 once only, so that the sum of the 3 numbers in any direction is always 21.
4. It saves a lot of time if one does not have to solve a problem with pencil and paper every time. That is why it is so important that you must be able to think quickly! Work on your own and complete the arithmetic test as quickly and accurately as possible. You have only three minutes!
a) 17 + 9 = _________________
b) 57 + 9 = _________________
c) 45 – 11 = _________________
d) 65 - 21 = _________________
e) Double 47: _________________
f) 17 + 19 + 13 = _________________
g) 23 + 19 + 7 = _________________
h) 210 + 120 + 21 = _________________
i) Double 184: _________________
j) 10 000 – 16 = _________________
k) Halve 64: _________________
l) Halve 96: _________________
m) 6 × 8 = _________________
n) 54 ÷ 9 = _________________
o) One quarter of 96 = _________________
p) 12 × 8 = _________________
q) _________________ ÷ 12 = 11
r) 63 ÷ _________________ = 9
s) (15 ÷ 15) × 15 = _________________
t) (56 + 63) + 44 = 56 + (_________________ + 63)
| HOW DID YOU FARE? | ||||||
| MARK THE RELEVANT BOX: |
| I had all right! | |
| I had more than half right! | |
| I did not do well enough. |
5. Now let us add even greater numbers. See if you can complete the following neatly and correctly. Start at 33 000 and add 10 000 at a time. Build yourself a "footpath" by colouring every block with the correct answer green.
| 33 000 | 40 000 | 58 000 | 85 000 | 93 000 | 102 000 | 110 000 | 133 000 |
| 38 000 | 43 000 | 60 000 | 83 000 | 96 000 | 103 000 | 111 000 | 123 000 |
| 41 000 | 53 000 | 62 000 | 73 000 | 99 000 | 107 000 | 113 000 | 121 000 |
| 32 000 | 55 000 | 63 000 | 71 000 | 100 000 | 109 000 | 116 000 | 119 000 |
DO YOU STILL REMEMBER?
If we want to programme the calculator to check the previous sum, we key in 33 000 + 10 000 = = =.
Use your calculator to check whether your “footpath” has been calculated correctly.
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.1: We know this when the learner counts forwards and backwards in whole number intervals and fractions;
Assessment Standard 1.8: We know this when the learner estimates and calculates by selecting and using operations appropriate to solving problems;
Assessment Standard 1.9: We know this when the learner We know this when the learner performs mental calculations.

Notification Switch
Would you like to follow the 'Mathematics grade 5' conversation and receive update notifications?