1.11 Least squares estimation in hilbert spaces  (Page 32/2)

Projections with orthonormal bases

Having an orthonormal basis for the subspace of interest significantly simplifies the projection operator.

Lemma 1 Let $x\in X$ , a Hilbert space, and let $S$ be a subspace of $X$ . If $\{b_1,b_2,...\}$ is an orthonormal basis for $S$ , then the closest point $s_0\in S$ to $x$ is given by $s_0={\sum }_i⟨x,b_i⟩b_i$ .

We begin by noting that

Now, since $s_0$ is the projection of $x$ onto $S$ , we must have that $x-s_0\perp S$ , and so for each basis element $b_i$ we must have $⟨x-s_0,b_i⟩=0$ . Additionally, since $s_0\in S$ and $\{b_1,b_2,...\}$ is an orthonormal basis for $S$ , we must have that ${\sum }_i⟨s_0,b_i⟩b_i=s_0$ . Thus, we obtain

proving the lemma.

Application: communications receiver

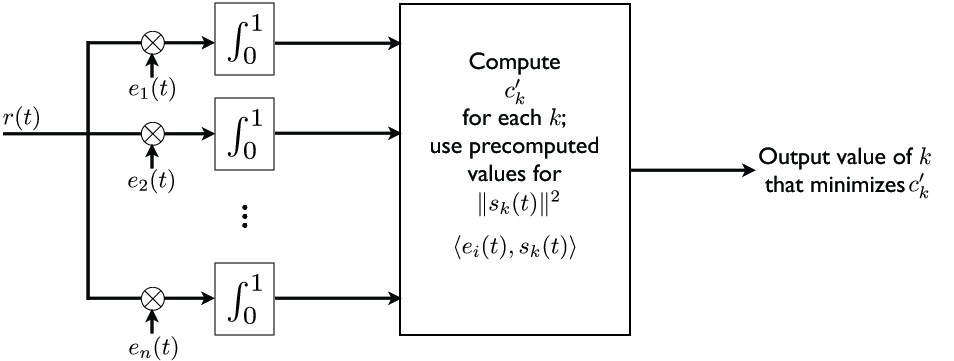
Consider the case of a communications receiver that records a continuous-time signal $r\left(t\right)=s\left(t\right)+n\left(t\right)$ over $0\le t\le 1$ , where $s\left(t\right)$ is one of $m$ codeword signals $\{s_1\left(t\right),...,s_m\left(t\right)\}$ , and $n\left(t\right)$ is additive white Gaussian noise. The receiver must make the best possible decision on the observed codeword given the reading $r\left(t\right)$ ; this usually involves removing as much of the noise as possible from $r\left(t\right)$ .

We analyze this problem in the context of the Hilbert space $L_2[0,1]$ . To remove as much of the noise as possible, we define the subspace $S=\mathrm{span}\left(\{s_1\left(t\right),...,s_m\left(t\right)\}\right)$ . Anything that is not contained in this subspace is guaranteed to be part of the noise $n\left(t\right)$ . Now, to obtain the projection into $S$ , we need to find an orthonormal basis $\{e_1\left(t\right),...,e_n\left(t\right)\}$ for $S$ , which can be done for example by applying the Gram-Schmidt procedure on the vectors $\{s_1\left(t\right),...,s_m\left(t\right)\}$ . The projection is then obtained according to the lemma as

where $⟨r\left(t\right),e_i\left(t\right)⟩={\int }_0^{1}r\left(t\right)e_i\left(t\right)dt$ .

After the projection is obtained, an optimal receiver proceeds by finding the value of $k$ that minimizes the distance

note here that the first term does not depend on $k$ , so it suffices to find the value of $k$ that minimizes the “cost”

In practice, the codeword signals are designed so that their norms $\parallel s_k{\left(t\right)\parallel }_2=\sqrt{⟨s_k\left(t\right),s_k\left(t\right)⟩}$ are all equal. This design choice reduces the problem above to finding the value of $k$ that maximizes the score

Thus, the receiver can be designed according to the diagram in [link] .

Least squares approximation in hilbert spaces

Let $y_1,...,u_n$ be elements of a Hilbert space $X$ and define the closed, finite-dimensional subspace of $X$ given by $S=\mathrm{span}(y_1,...,y_n)$ . We wish to find the best approximation of $x$ in terms of the vectors $y_i$ , that is, the linear combination ${\sum }_{i=1}^n{a}_i{y}_i$ with the smallest error $e=x-{\sum }_{i=1}^n{a}_i{y}_i$ . To measure the size of the error, we use the induced norm $\parallel e\parallel =∥x,-,{\sum }_{i=1}^n,a_i,y_i∥$ .

To solve this problem, we rely on the projection theorem: we are indeed looking for the closest point to $x$ in $S=\mathrm{span}(y_1,...,y_n)$ . The projection theorem tells us that the closest point $s_0={\sum }_{i=1}^n{a}_i{y}_i$ must give $x-s_0\perp S$ , i.e., $e\perp S$ , which implies in turn that $〈x,-,{\sum }_{i=1}^n,a_i,y_i,,,y_j〉=0$ for all $j=1,...,n$ . The requirement can be rewritten as $⟨x,y_j⟩=〈{\sum }_{i=1}^n,a_i,y_i,,,y_j〉={\sum }_{i=1}^n{a}_i⟨y_i,y_j⟩$ for each $j=1,...,n$ . These requirements can be collected and written in matrix form as