| << Chapter < Page | Chapter >> Page > |
Eliminate the parameter for each of the plane curves described by the following parametric equations and describe the resulting graph.
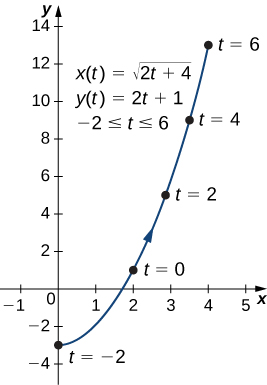
Eliminate the parameter for the plane curve defined by the following parametric equations and describe the resulting graph.
or
This equation describes a portion of a rectangular hyperbola centered at
So far we have seen the method of eliminating the parameter, assuming we know a set of parametric equations that describe a plane curve. What if we would like to start with the equation of a curve and determine a pair of parametric equations for that curve? This is certainly possible, and in fact it is possible to do so in many different ways for a given curve. The process is known as parameterization of a curve .
Find two different pairs of parametric equations to represent the graph of
First, it is always possible to parameterize a curve by defining then replacing x with t in the equation for This gives the parameterization
Since there is no restriction on the domain in the original graph, there is no restriction on the values of t.
We have complete freedom in the choice for the second parameterization. For example, we can choose The only thing we need to check is that there are no restrictions imposed on x ; that is, the range of is all real numbers. This is the case for Now since we can substitute for x. This gives
Therefore, a second parameterization of the curve can be written as

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?