| << Chapter < Page | Chapter >> Page > |
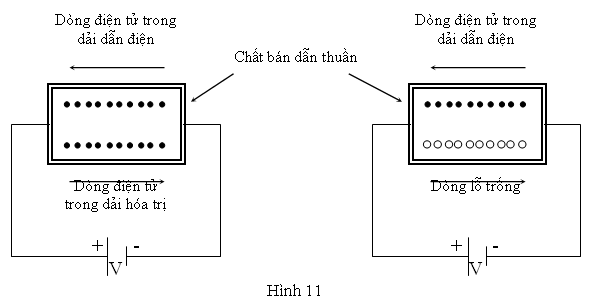
Tương ứng với những dòng điện này, ta có những mật độ dòng điện J, Jn, Jp sao cho: J = Jn+Jp
Ta đã chứng minh được trong kim loại:
J = n.e.v = n.e..E
Tương tự, trong chất bán dẫn, ta cũng có:
Jn=n.e.vn=n.e. n.E (Mật độ dòng điện trôi của điện tử, n là độ linh động của điện tử, n là mật độ điện tử trong dải dẫn điện)
Jp=p.e.vp=p.e.p.E (Mật độ dòng điện trôi của lỗ trống, p là độ linh động của lỗ trống, p là mật độ lỗ trống trong dải hóa trị)
Như vậy: J=e.(n.n+p.p).E
Theo định luật Ohm, ta có:
J = .E
=> = e.(n.n+p.p) được gọi là dẫn suất của chất bán dẫn.
Trong chất bán dẫn loại N, ta có n>>p nên n = n.n.e
Trong chất bán dẫn loại P, ta có p>>n nên p = n.p.e
Dưới tác dụng của điện trường, các điện tử và lỗ trống di chuyển với vận tốc trung bình vn=n.E và vp=p.E.
Số điện tử và lỗ trống di chuyển thay đổi theo mỗi thời điểm, vì tại mỗi thời điểm có một số điện tử và lỗ trống được sinh ra dưới tác dụng của nhiệt năng. Số điện tử sinh ra trong mỗi đơn vị thời gian gọi là tốc độ sinh tạo g. Những điện tử này có đời sống trung bình n vì trong khi di chuyển điện tử có thể gặp một lỗ trống có cùng năng lượng và tái hợp với lỗ trống này. Nếu gọi n là mật độ điện tử, trong một đơn vị thời gian số điện tử bị mất đi vì sự tái hợp là n/n. Ngoài ra, trong chất bán dẫn, sự phân bố của mật độ điện tử và lỗ trống có thể không đều, do đó có sự khuếch tán của điện tử từ vùng có nhiều điện tử sang vùng có ít điện tử.
Xét một mẫu bán dẫn không đều có mật độ điện tử được phân bố như hình vẽ. Tại một điểm M trên tiết diện A, số điện tử đi ngang qua tiết diện này (do sự khuếch tán) tỉ lệ với dn/dx, với diện tích của điện tử và với tiết diện A.
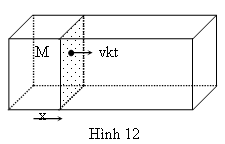
Dòng điện khuếch tán của điện tử đi qua A là:
Dn được gọi là hằng số khuếch tán của điện tử.
Suy ra mật độ dòng điện khuếch tán của điện tử là:
Tương tự, trong một giây có lỗ trống bị mất đi, với p là mật độ lỗ trống và p là là đời sống trung bình của lỗ trống.
Dòng điện khuếch tán của lỗ trống trong mẫu bán dẫn trên là:
Và mật độ dòng điện khuếch tán của lỗ trống là:
Người ta chứng minh được rằng:
Với: K là hằng số Boltzman = 1,382.10-23J/0K
T là nhiệt độ tuyệt đối.
Hệ thức này được gọi là hệ thức Einstein.
Ở nhiệt độ bình thường (3000K): VT=0,026V=26mV
Xét một hình hộp có tiết diện A, chiều dài dx đặt trong một mẩu bán dẫn có dòng điện lỗ trống Ip đi qua. Tại một điểm có hoành độ x, cường độ dòng điện là Ip. Tại mặt có hoành độ là x+dx, cường độ dòng điện là Ip+dIp. Gọi P là mật độ lỗ trống trong hình hộp, p là đời sống trung bình của lỗ trống. Trong mỗi giây có lỗ trống bị mất đi do sự tái hợp. Vậy mỗi giây, điện tích bên trong hộp giảm đi một lượng là:
(do tái hợp)
Đồng thời điện tích trong hộp cũng mất đi một lượng:
G2=dIp (do khuếch tán).
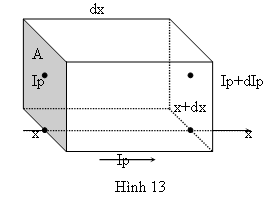
Gọi g là mật độ lỗ trống được sinh ra do tác dụng nhiệt, trong mỗi giây, điện tích trong hộp tăng lên một lượng là:
T1=e.A.dx.g
Vậy điện tích trong hộp đã biến thiên một lượng là:
Độ biến thiên đó bằng:
Vậy ta có phương trình:
(1)
Nếu mẩu bán dẫn ở trạng thái cân bằng nhiệt và không có dòng điện đi qua, ta có:
dIp=0; P=P0=hằng số
Phương trình (1) cho ta:
Với P0 là mật độ lỗ trống ở trạng thái cân bằng nhiệt. Thay trị số của g vào phương trình (1) và để ý rằng p và IP vẫn tùy thuộc vào thời gian và khoảng cách x, phương trình (1) trở thành:
(2)
Gọi là phương trình liên tục.
Tương tự với dòng điện tử In, ta có:
(3)
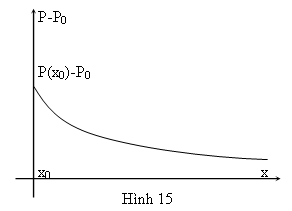
TD: ta giải phương trình liên tục trong trường hợp p không phụ thuộc vào thời gian và dòng điện Ip là dòng điện khuếch tán của lỗ trống.
Ta có: và
Do đó,
Phương trình (2) trở thành:
Trong đó, ta đặt
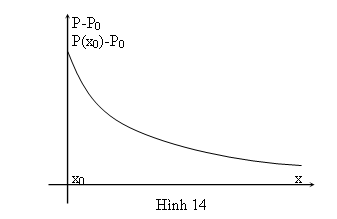
Nghiệm số của phương trình (4) là:
Vì mật độ lỗ trống không thể tăng khi x tăng nên A1 = 0
Do đó: tại x = x0.
Mật độ lỗ trống là p(x0),
Do đó:
Suy ra, nghiệm của phương trình (4) là:

Notification Switch
Would you like to follow the 'Điện tử ứng dụng' conversation and receive update notifications?