| << Chapter < Page | Chapter >> Page > |
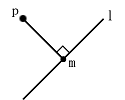
Given a line 'l' and a point 'p' in the plane, what's the closest point 'm' to 'p' on 'l'?
Same problem: Let and be vectors in . Say . For what value of is minimized? (what point in span{v} best approximates ?)
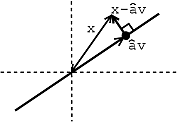
The condition is that and are orthogonal .
How to calculate ?
We know that ( ) is perpendicular to every vector in span{v}, so because , so Closest vector in span{v} = , where is the projection of onto .
Point to a plane?
We can do the same thing in higher dimensions.
Let be a subspace of a Hilbert space H. Let be given. Find the that best approximates . i.e., is minimized.
, , . So,
V = {space of periodic signals with frequency no greater than }. Given periodic f(t), what is the signal in V that best approximates f?
Let V = {functions piecewise constant between the integers}
where { } is an ONB.
Best piecewise constant approximation?
This demonstration explores approximation using a Fourier basis and a Haar Wavelet basis.See here for instructions on how to use the demo.

Notification Switch
Would you like to follow the 'Ee textbook' conversation and receive update notifications?