0.9 Непрекинатост на функција

Непрекинатост на функција

Дефиниција.

Функцијата $y=f(x)$ е непрекината во точката $x=a$ ако се исполнети следните три услови:

1 ⁰ $f(x)$ е дефинирана во точката $x=a$ ,

2 ⁰ постои $\underset{x\to a}{\text{lim}}f(x)=A$ ,

3 ⁰ $\underset{x\to a}{\text{lim}}f(x)=f(a)=A$ .

Од дефиницијата за непрекинатост на функција следува дека функцијата $f(x)$ е непрекината во точката $x=a$ ако е дефинирана во таа точка, ако постои гранична вредност во таа точка и ако таа граница е еднаква со вредноста на функцијата во истата точка. Обратното не мора да важи, бидејки функцијата може да има граница во точката $x=a$ , а да не е дефинирана во истата точка.

Затоа функцијата $f(x)$ ќе биде прекината во точката $x=a$ ако еден или повеќе услови од дефиницијата за непрекинатост не се исполнети.

Пример 1.

За која вредност на константата $a$ функцијата ќе биде непрекината?

РЕШЕНИЕ:

Функцијата $f(x)$ е составена од полиномни функции за кои нема ограничување во дефиниционата област и како такви се непрекинати во интервалите на кои се зададени, a единствено треба да се провери граничната точка која ги дели интервалите на нивното дефинирање. Првата функција е дефинирана и непрекината на интервалот , а втората на $x>1$ и затоа единствено треба да се провери граничната точка меѓу овие интервали $x=1$ .

Се пресметува вредноста на функцијата во оваа точка

$f(1)=(x+1){/}_{x=1}1+1=2$ ,

а за пресметување на границата во оваа точка користиме еднострани граници, бидејќи за помали и поголеми вредности од $x=1$ функциите се различно дефинирани.

Се пресметува левата граница

$\underset{x\to 1^{-}}{\text{lim}}f(x)=\underset{x\to 1^{-}}{\text{lim}}(x+1)=2$ ;

додека десната граница е

$\underset{x\to 1^{+}}{\text{lim}}f(x)=\underset{x\to 1^{+}}{\text{lim}}(3-{\text{ax}}^2)=3-a$ .

Од дефиницијата за непрекинатост, за да функцијата биде непрекината во точка потребно е во таа точка да има граница која е еднаква со вредноста на функцијата во точката. Во овој пример вредноста на функцијата е еднаква со левата граница, а останува уште таа вредност да е еднаква и на десната граница.

Овој услов го дава равенството

$3-a=2\Rightarrow a=1$ ,

што значи дека вредноста на константата треба да биде

$a=1$ за да функцијата $f(x)$ биде непрекината.

Неколку видови на непрекинатост на функција ќе се прикажат низ примери.

Пример 2.

Функцијата $f(x)=\frac{1}{x}$ е прекината во точката $x=0$ бидејќи $f(0)$ не постои $(0\notin D_f)$ и едностраните граници се бесконечни:

$\underset{x\to 0^{+}}{\text{lim}}\frac{1}{x}=\frac{1}{0+}\text{=+}\infty$ ,

$\underset{x\to 0^{-}}{\text{lim}}\frac{1}{x}=\frac{1}{0-}=-\infty$ .

Оваа функција (Сл.1) е непрекината во сите точки освен во $x=0$ и се вели дека во неа има бесконечен прекин . Графикот на функцијата има ,, скок “ во таа таа точка, односно вредностите на функцијата добиени лево од точката на прекин скокаат до вредностите десно од точката на прекин.

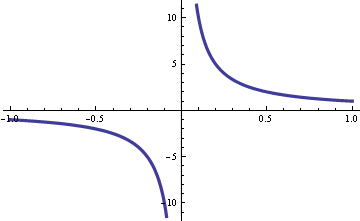Слика 1 График на функцијата $f(x)=\frac{1}{x}$

Пример 3.

Функцијата $f(x)=\frac{x^2-9}{x-3}$ е прекината во точката $x=3$ , бидејќи $f(3)$ не е постои, додека $\underset{x\to 3}{\text{lim}}\frac{x^2-9}{x-3}=6$ .

Овој вид прекин може да отстрани преку редефинирање на функцијата со

Функциите $f(x)=\frac{x^2-9}{x-3}$ и $g(x)=x+3$ се идентични освен во точката $x=3$ во која за функцијата $f(x)=\frac{x^2-9}{x-3}$ се формира “дупка” (јама) (Сл. 2).

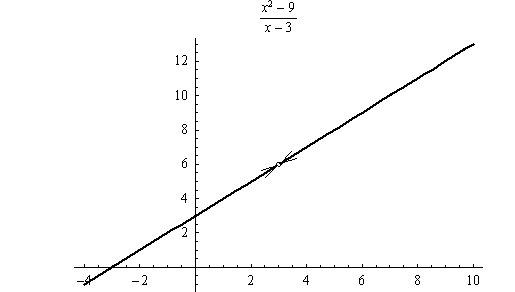Слика 2. График на функцијта $f(x)=\frac{x^2-9}{x-3}$

Пример 4.

Функцијата е дефинирана во точката $x=1$ , $f(1)=2$ , но има различни еднострани граници во неа:

и затоа функцијата е прекината во точката $x=1$ .

Особини на непрекинатите функции

Непрекинатите функции се многу важна класа функции. За нив важат следните особини:

• Ако функциите $f(x)$ и $g(x)$ се непрекинати во точката $x=a$ , тогаш и функциите се исто така непрекинати функции истата точка.
• Ако функцијата е непрекината во сите точки од еден интервал, тогаш таа е непрекината на целиот интервал.
• За да непрекината функција премине од една своја вредност во друга, таа мора да ги прими сите вредности меѓу овие две вредности.
• Ако непрекината функција во околина на дадена точка има вредност различна од нула, тогаш околу таа точка ќе постои интервал во кој функцијта има ист знак со вредноста на функцијата.
• Ако на краевите од еден интервал функцијата има вредности различни по знак, тогаш ќе постои барем една точка од внатрешноста на интервалот во која функцијата ќе има вредност нула.

Непрекинатоста кај елементарните функции е следна: полиномот е непрекината функција за секоја реална вредност на аргументот, дробнорационалните функции се непрекинати во сите точки освен во нулите на именителот во кои точки функцијата не е дефинирана. Експоненцијалната функција е непрекината за секоја вредност на аргументот. Логаритамската функција е непрекината за сите позитивни вредности на аргументот. Тригонометриските функции $y=\text{sin}x,y=\text{cos}x$ се непрекинати за секоја реална вредност на аргументот, функцијата $y=\text{tg}x$ е непрекината за сите , додека $y=\text{ctg}x$ е непрекината за . Инверзните тригонометриски функции $y=\text{arcsin}x,y=\text{arccos}x$ се непрекинати на интервалот [-1, 1], додека $y=\text{arctg}x,y=\text{arcctg}x$ се непрекинати за секоја реална вредност на аргументот.