0.9 Bộ nhớ ảo  (Page 9/13)

Dĩ nhiên, số lượng bit lịch sử có thể khác nhau và có thể được chọn (phụ thuộc phần cứng sẳn có) để thực hiện cập nhật nhanh nhất có thể. Trong trường hợp cực độ, số có thể được giảm về 0, chỉ bit tham khảo chính nó. Giải thuật này được gọi là giải thuật thay thế trang cơ hội thứ hai (second-chance page-replacement algorithm).

Giải thuật cơ hội thứ hai

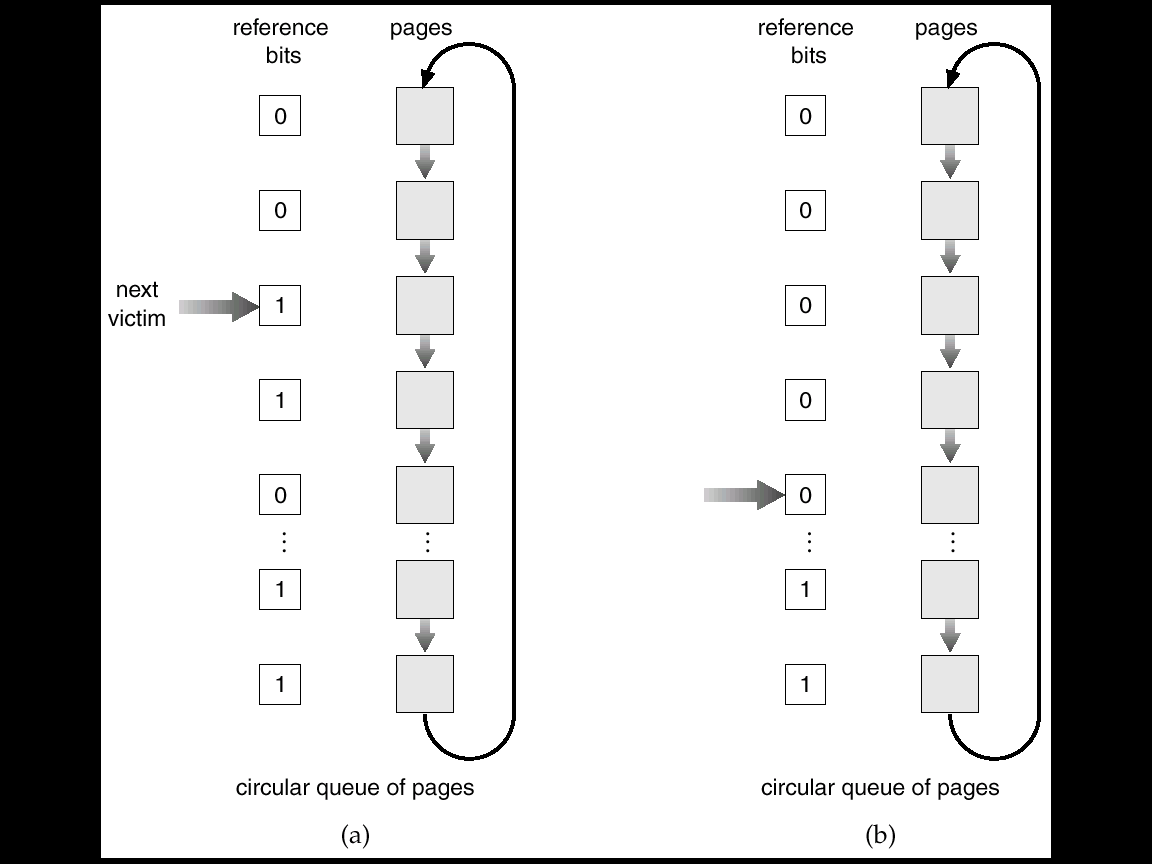
Hình VIII‑12 giải thuật thay thế trang cơ hội thứ hai

Giải thuật thay thế trang cơ hội thứ hai cơ bản là giải thuật thay thế FIFO. Tuy nhiên, khi một trang được chọn, chúng ta xét bit tham khảo của nó. Nếu giá trị bit này là 0, chúng ta xử lý để thay thế trang này. Tuy nhiên, nếu bit tham khảo được đặt tới 1, chúng ta cho trang đó một cơ hội thứ hai và di chuyển để chọn trang FIFO kế tiếp. Khi một trang nhận cơ hội thứ hai, bit tham khảo của nó được xoá và thời gian đến của nó được đặt lại là thời gian hiện hành. Do đó, một trang được cho cơ hội thứ hai sẽ không được thay thế cho đến khi tất cả trang khác được thay thế (hay được cho cơ hội thứ hai). Ngoài ra, nếu một trang được dùng đủ thường xuyên để giữ bit tham khảo của nó được đặt, nó sẽ không bao giờ bị thay thế.

Một cách để cài đặt giải thuật cơ hội thứ hai như một hàng đợi vòng. Một con trỏ hiển thị trang nào được thay thế tiếp theo. Khi một khung được yêu cầu, con trỏ tăng cho tới khi nó tìm được trang với bit tham khảo 0. Khi nó tăng, nó xoá các bit tham khảo (hình VIII-12). Một khi trang nạn nhân được tìm thấy, trang được thay thế và trang mới được chèn vào hàng đợi vòng trong vị trí đó. Chú ý rằng, trong trường hợp xấu nhất khi tất cả bit được đặt, con trỏ xoay vòng suốt toàn hàng đợi, cho mỗi trang một cơ hội thứ hai. Thay thế cơ hội thứ hai trở thành thay thế FIFO nếu tất cả bit được đặt.

Giải thuật cơ hội thứ hai nâng cao

Chúng ta có thể cải tiến giải thuật cơ hội thứ hai bằng cách xem xét cả hai bit tham khảo và sửa đổi như một cặp được xếp thứ tự. Với hai bit này , chúng ta có 4 trường hợp có thể:

1. (0,0) không được dùng mới đây và không được sửa đổi-là trang tốt nhất để thay thế.
2. (0,1) không được dùng mới đây nhưng được sửa đổi-không thật tốt vì trang cần được viết ra trước khi thay thế.
3. (1,0) được dùng mới đây nhưng không được sửa đổi-nó có thể sẽ nhanh chóng được dùng lại.
4. (1,1) được dùng mới đây và được sửa đổi-trang có thể sẽ nhanh chóng được dùng lại và trang sẽ cần được viết ra đĩa trước khi nó có thể được thay thế.

Khi thay thế trang được yêu cầu, mỗi trang ở một trong bốn trường hợp. Chúng ta dùng cùng một cơ chế như giải thuật đồng hồ, nhưng thay vì xem xét trang chúng ta đang trỏ tới có bit tham khảo được đặt tới 1 hay không, chúng ta xem xét trường hợp mà trang đó đang thuộc về. Chúng ta thay thế trang đầu tiên được gặp trong trường hợp thấp nhất không rỗng. Có thể chúng ta phải quét hàng đợi vòng nhiều lần trước khi chúng ta tìm một trang được thay thế.

Giải thuật này được dùng trong cơ chế quản lý bộ nhớ ảo của Macintosh. Sự khác nhau chủ yếu giữa giải thuật này và giải thuật đồng hồ đơn giản hơn là chúng ta cho tham khảo tới các trang đó mà chúng được sửa đổi để cắt giảm số lượng nhập/xuất được yêu cầu.