0.8 Complex numbers

Complex numbers

Introduction

It is essential that engineers master the concept of complex numbers because the important role that complex numbers play in a variety of application areas. In this module applications in the field of electric circuits are provided.

Alternating current (ac) electric circuits

Earlier we introduced a number of components that are typically found in common electric circuits. These included voltage sources, current sources and resistors. We also observed that the behavior of an electric circuit could be predicted by using several laws from Physics, including Ohm’s Law and Kirchoff’s Laws.

In this laboratory exercise, we will introduce two additional components of electric circuits: the inductor and the capacitor. These elements are typically found in electric circuits which involve sinusoidally varying voltage or current sources. These circuits are called alternating current or AC circuits. AC circuits abound in the physical world. The voltage and current that power household appliances comes from AC sources.

Figure 1 shows the plot for a sinusoidally varying waveform that represents the output of an AC voltage source. Such a waveform could also be used to represent the current that is supplied by an AC current source. It is important to note that the waveform has a repetitive or periodic nature.

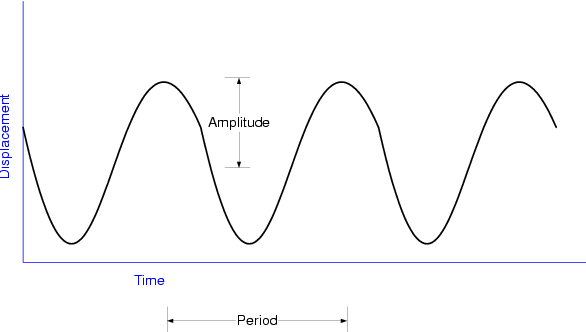
In the figure, we note that the amount of time that occurs between successive maxima of the sinusoidal waveform is equal to the period . The angular frequency of the waveform is denoted by the symbol ω and is defined in terms of the period by the equation

If we denote the amplitude as V max , then we can express the sinusoidal waveform for the voltage mathematically as

Here the instantaneous value of the voltage is measured in the units volts. The term θ v is called the phase angle of the sinusoidal waveform. It is measured in degrees. Its usage and importance in the analysis of AC circuits will be discussed later in the course during the study of trigonometry.

Inductors and capacitors are found in circuits of all types and designs, so their understanding is critical to the education of an engineer or scientist. One important distinction between resistors and these two new components (inductors and capacitors) is that they are analyzed using different mathematic techniques. In the case of a resistor, it was quite easy to determine the relationship between the current, voltage and resistance present in a circuit by means of simple algebra. In the case of the inductor and the capacitor, we will see that we must expand our knowledge of mathematics particulary in the are of complex numbers to analyze circuits that contain inductors and capacitors.