0.7 Radicals  (Page 2/2)

The presence of ice on the wings and fuselage on an aircraft can lead to severe problems during stormy winter weather. Equipment is used to spray aircraft with a de-icing agent prior to take-off in order to remove the ice from the wing surfaces and fuselage of planes.

There are several important parameters that relate to the performance of a nozzle. These include the diameter of the nozzle ( d ), the nozzle pressure ( P ) and the flow rate ( r ). The nozzle diameter is measured in inches; the flow rate is measured in gallons/minute; and the nozzle pressure is measured in pounds/square inch. The relationship between these parameters can be expressed via the radical equation

Question: Water flows at a rate of 2.5 pounds/s through a nozzle whose diameter is 0.25 inches. What is the value of the nozzle pressure at the exit?

Solution: We can begin by substituting values into equation (5).

This can be written as

Squaring each side of the equation yields the result $P=1\text{.}\text{778}\text{lb}/{\text{in}}^2$

Motion of a pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting or equilibrium point, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force combined with the pendulum's mass causes it to swing back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. A pendulum swings with a specific period which depends on factors such as its length. From its discovery around 1602 by Galileo, the regular motion of pendulums was used for timekeeping, and was the world's most accurate timekeeping technology until the 1930s.

Figure 3 shows a picture of a pendulum.

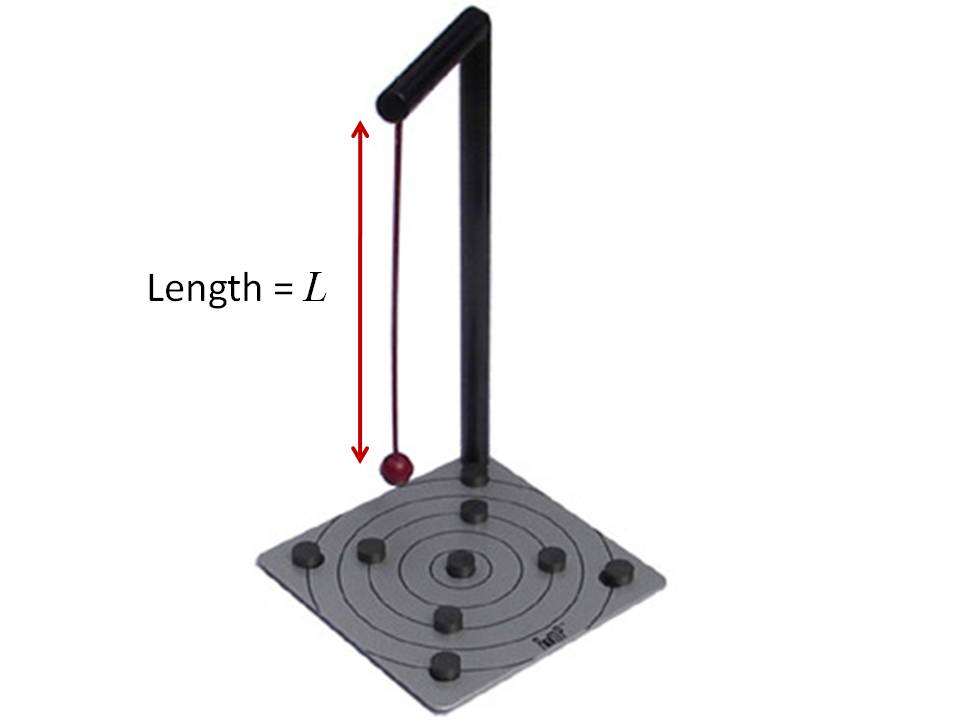
The period of the pendulum can be represented by the variable T . The period is typically measured in seconds. The length of the pendulum can be modeled by the variable L and is measured in feet. Under such conditions, the relationship between the period and the length of the pendulum is summarized by the equation

Question: The arm of a pendulum makes a complete cycle every two seconds. What is the length of the pendulum?

Solution: We insert the appropriate value for the period into equation (9)

Next, we square each side of the equation

which can be re-arranged as

So our solution is $L=3\text{.}\text{24}\text{ft}$

Exercises

1. Use algebra to derive a formula that expresses F as a function of T, m and R.
2. A passenger rides around in a ferris wheel of radius 20 m which makes 1 revolution every 10 seconds. If the passenger has a mass of 75 kg, what is the centripetal force exerted on the passenger? (Use the formula you derived in Exercise 1 to solve for the centripetal force.)
3. Find the centripetal force exerted on the passenger described in Exercise 2 if the ferris wheel takes 8 seconds to complete one revolution.
4. What can you say qualitatively about the relationship between the centripetal force and the amount of time it takes to complete one revolution?
5. Apply algebra to equation (3) to produce a formula for P as a function of r and d .
6. Find the nozzle pressure P for a nozzle whose diameter is 1.25 inches for a flow rate of 250 gallons/minute.
7. Find the nozzle pressure P for a nozzle whose diameter is 1.50 inches for a flow rate of 250 gallons/minute.
8. What can you say qualitatively about the relationship between the pressure P and the diameter of the nozzle d ?
9. A grandfather clock has a pendulum of length 3.5 feet. How long will it take for the pendulum to swing back and forth one time?
10. To achieve a period of 2 seconds, how long must a pendulum be?