0.5 Why does α depend on the cutoff frequency?

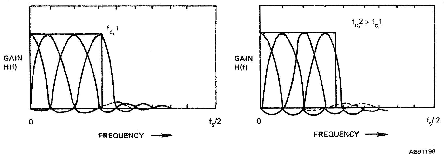
The formulas presented in Equation 1 and Equation 2 from the module titled "Filter Sizing" imply that $\alpha$ and hence the required filter order $N$ are independent of the cutoff frequency $f_c$ . The supporting analysis showed that this is only true in the limit of high order filters,i.e. when $N$ is large. The dependence for shorter filters is shown in Figure 2 from the module titled "Filter Sizing" . Why should this occur? Consider the filterdesign problem shown in [link] . Again the goal is a simple lowpass filter with cutoff frequency $f_c$ . The frequency sampling points at frequency multiples of $\frac{f_s}{N}$ are also shown as solid dots. Instead of fixing the gains we presume that the filter gains ${\widehat{h}}_n$ , or, equivalently, the graphic equalizer levers, are optimized, by whatevermeans, to yield the best stopband ripple performance.

[link] (a) shows the combination of gains ${\widehat{h}}_n$ needed to constrain the peak stopband ripple to a given level, say $\overline{{\delta }_2}$ . The frequency at which this equal ripple band starts is of course $f_{st}$ and the difference between $f_{st}$ and $f_c$ is $\Delta f$ . Now suppose that $f_c$ is increased slightly, as shown in [link] (b). Now a different set of the ${\widehat{h}}_n$ are needed to make the peak ripple equal $\overline{{\delta }_2}$ and these result in different values of $f_{st}$ and $\Delta f$ . Pursuing this graphical analysis we find that:

• Cutoff frequencies near multiples of $\frac{f_s}{N}$ result in smaller transition bands, and hence smaller values of $\alpha$ , than those near the center of two bins. This occurs, to first order, sincetwo or more stopband basis filters are needed to cancel the first sidelobe of the last basis passband filter when the passbandstops between two bins, while one is needed if the passband stops near a bin.
• Because these “hard" and “easy" frequency ranges occur for every bin, the number of the ranges, counting both positive andnegative frequencies, is about the same as the filter order Various boundary conditions can make the actual number one less or one more than the filter order. $N$ .
• The variation in the transition band $\Delta f$ is more pronounced as $N$ decreases since there are fewer basis filters to use in optimizing the response.

As an aside one might observe from Figure 1 from the module titled Performance Comparison with other FIR Design Methods that all three methods perform about equally for high levels of stopband ripple.Intuitively the reason for this should now be clear. Window-based methods need not use much shaping if high levels of ripple are tolerable.Similarly, frequency sampling need not use many adjustable coefficients.Since this is true the equal-ripple techniques will not perform much better since their only advantage is that of adjusting all of the filter gains.The underlying point is that, for high-ripple designs, all of the methods produce designs closely resembling the sum of simple, shifted $\frac{sinNq}{sinq}$ functions and produce a transition band $\Delta f$ of about the order of $\frac{f_s}{N}$ , hence an $\alpha$ of about unity. Only as the stopband ripple specification grows tighter does the method and accuracy of adjusting the coefficients and the numberof them available for adjustment begin to affect the transition band performance.