0.5 6.6 inelastic collisions in one dimension  (Page 2/5)

Solution for (a)

Momentum is conserved because the net external force on the puck-goalie system is zero.

Conservation of momentum is

or

Because the goalie is initially at rest, we know $v_2=0$ . Because the goalie catches the puck, the final velocities are equal, or ${v\prime }_1={v\prime }_2=v\prime$ . Thus, the conservation of momentum equation simplifies to

Solving for $v\prime$ yields

Entering known values in this equation, we get

Discussion for (a)

This recoil velocity is small and in the same direction as the puck’s original velocity, as we might expect.

Solution for (b)

Before the collision, the internal kinetic energy ${\text{KE}}_{\text{int}}$ of the system is that of the hockey puck, because the goalie is initially at rest. Therefore, ${\text{KE}}_{\text{int}}$ is initially

After the collision, the internal kinetic energy is

The change in internal kinetic energy is thus

where the minus sign indicates that the energy was lost.

Discussion for (b)

Nearly all of the initial internal kinetic energy is lost in this perfectly inelastic collision. ${\text{KE}}_{\text{int}}$ is mostly converted to thermal energy and sound.

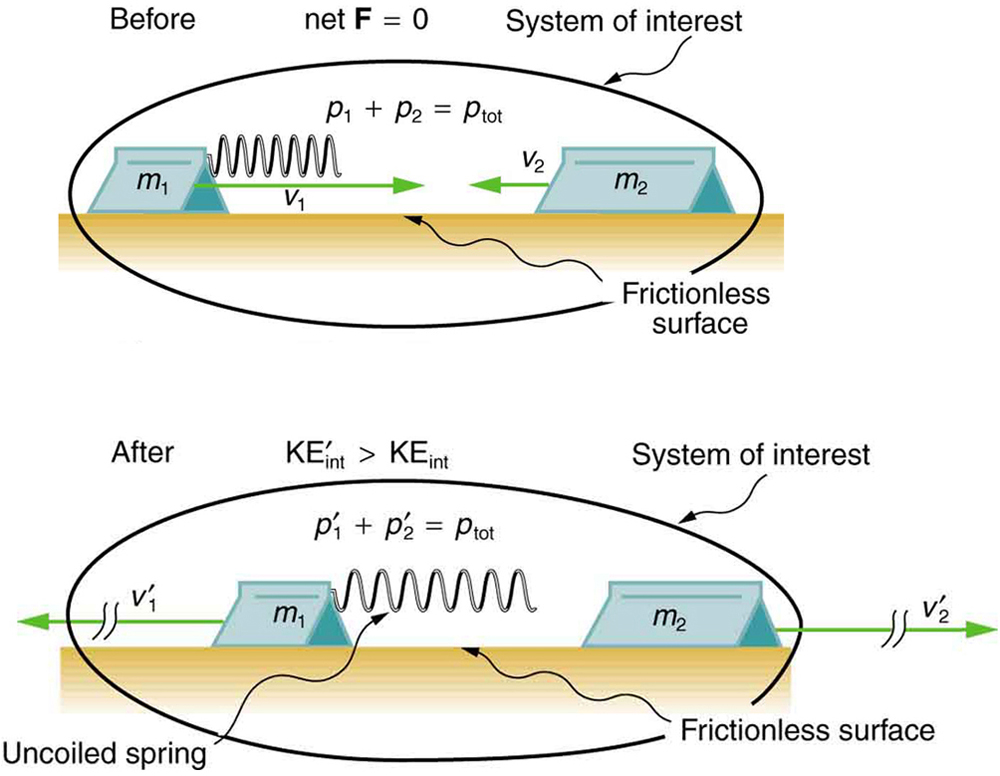
During some collisions, the objects do not stick together and less of the internal kinetic energy is removed—such as happens in most automobile accidents. Alternatively, stored energy may be converted into internal kinetic energy during a collision. [link] shows a one-dimensional example in which two carts on an air track collide, releasing potential energy from a compressed spring. [link] deals with data from such a collision.

Collisions are particularly important in sports and the sporting and leisure industry utilizes elastic and inelastic collisions. Let us look briefly at tennis. Recall that in a collision, it is momentum and not force that is important. So, a heavier tennis racquet will have the advantage over a lighter one. This conclusion also holds true for other sports—a lightweight bat (such as a softball bat) cannot hit a hardball very far.

The location of the impact of the tennis ball on the racquet is also important, as is the part of the stroke during which the impact occurs. A smooth motion results in the maximizing of the velocity of the ball after impact and reduces sports injuries such as tennis elbow. A tennis player tries to hit the ball on the “sweet spot” on the racquet, where the vibration and impact are minimized and the ball is able to be given more velocity. Sports science and technologies also use physics concepts such as momentum and rotational motion and vibrations.