| << Chapter < Page | Chapter >> Page > |
Tutorial on Chapter 1-Crystal and Crystal Growth.
Method:
FCC crystal has 8 atoms at the 8 corners of the cube and 6 atoms on the 6 faces (4 on side faces+2 on the upper and lower faces].
Therefore N = the coordination Number = the number of atoms per unit cell = (8×1/8+6×1/2)= 4 atoms per unit cell.
The atoms are solid spheres and are closely packed so that the atom at the center of the face are touching the 4 atoms on the four corners of the face as shown in the Figure I.
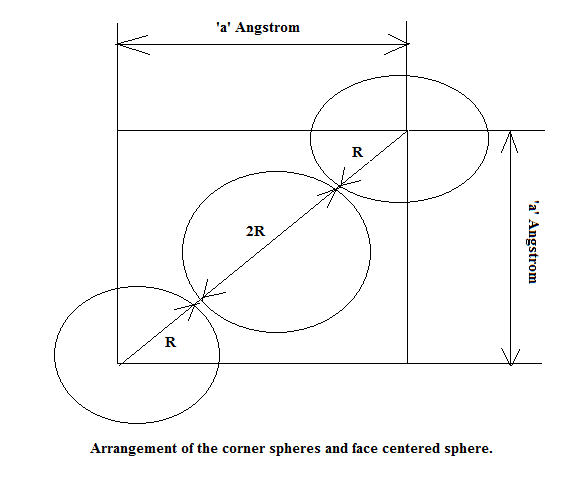
Inspecting the Figure we find that:
4R=diagonal of the face=a√2.
Therefore R/a = √2/4=1/(2√2)
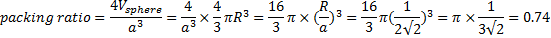
Therefore packing percentage in FCC crystals is 74%.
Method:
BCC crystal has 8 atoms at the 8 corners of the cube and 1 atom at the center of the Cube. Therefore N = the coordination Number = the number of atoms per unit cell = (8×1/8+1)= 2 atoms per unit cell.
The atoms are solid spheres and are closely packed so that the atom at the center of the Cube is touching the 2 atoms on the two corners of the cross diagonal of the cube as shown in the Figure 2.
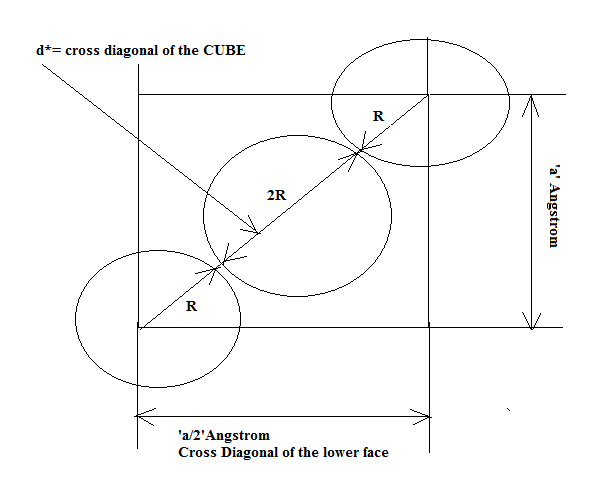
Inspecting the Figure we find that:
4R= cross diagonal of the Cube =a√3.
Therefore R/a = √3/4;
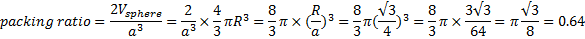
Therefore packing percentage in FCC crystals is 68%.
Copper is univalent crystal hence each atom contributes one electron. Therefore atomic density gives the conducting electron density.
Coordination Number of Cu = N = 4 atoms per unit cell.
Unit cell volume is a 3 .
Therefore atomic density = conducting electron density = 4 / (a 3 ) = 8.5734×10 28 /m 3 = 8.5734×10 22 /cc.
Find the weight density of Si,Ge and GaAs. Given Avogadro Number = N Avo =6.02×10 23 atoms/gm-mole, Si, Ge and GaAs have atomic weight of 28.1, 72.6 and 144.63(mean=72.315 respectively and the lattice parameters are 5.43A°, 5.646A° and 5.6533A° respectively.
[Ans. 2.33gm/cc, 5.37gm/cc and 5.32gm/cc respectively]
Method:
Coordination Number =N= 8 corner atoms + 6 face center atoms + 4 body center atoms= (1/8×8 + 1/2×6+ 4)= 8 atoms per unit cell.
Therefore Number density = N * = 8/a 3 = 4.9967×10 22 atoms/cc, 4.445 ×10 22 atoms/cc, 4.4277 ×10 22 atoms/cc,of Si, Ge and GaAs respectively.
Weight of one atom= (AW gm/mole)÷ (N Avo atoms/mole)= 4.66×10 -23 gm/atom. 1.157×10 -22 gm/atom. 1.244×10 -22 gm/atom of Si, Ge, GaAs respectively.
Therefore weight density = Wt of one atom× N * = Weight Density = ρ
Therefore density of Si=4.9967×10 22 atoms/cc×4.6677×10 -23 gm/atom=2.33gm/cc.

Notification Switch
Would you like to follow the 'Electrical and electronic materials science' conversation and receive update notifications?