0.4 Параметарски равенки на функција

Параметарски равенки на функција

При проучувањето на некои проблеми од физиката и механиката, функцијата $y=f(x)$ задедена во експлицитен или $F(x,y)=0$ во имплицитен облик не е погодна за проучување и затоа се воведува нова, трета помошна променлива $t$ преку која функцијата пооделно се разгледува на апсцисната и ординатната оска. Затоа функцијата се изразува преку нови равенки

$\begin{array}{}x=\varphi (t)\\ y=\psi (t)\text{.}\end{array}$

Помошната променлива $t$ во овие равенки се нарекува параметар , а вака зададената функција е во параметарски облик или со параметарски равенки .

Со елимини­рање на парамертарот $t$ од параметарски зададената функција, доколку е можно, функцијата може да се доведе во експлицитен облик $y=f(x)$ или имплицитен облик $F(x,y)=0$ , во коj директно се гледа зависноста на $y$ од $x$ .

Задача 1.

Во параметарски зададената функција

$\begin{array}{}x=\text{cos}t,\\ y=\text{sin}\mathrm{2t}\end{array}$

да се елиминира параметарот $t$ .

Решение:

Поаѓајќи од функцијата

$y=\text{sin}\mathrm{2t}$

и со нејзино квадрирање

$y^2=(\text{sin}\mathrm{2t}{)}^2=(2\text{cos}t\text{sin}t{)}^2=4{\text{cos}}^{2}t{\text{sin}}^{2}t=4{\text{cos}}^2(1-{\text{cos}}^{2}t)$ ,

и замена на

$x=\text{cos}t,$

се исклучува параметарот $t$ , при што се добива имплицитната функција

$y^2={\mathrm{4x}}^2(1-x^2)$ .

Задача 2.

Да се провери дека со параметарските равенки

$x=2+5\text{cos}t,y=-3+5\text{sin}t$

е зададена кружница.

Решение:

Равенката на кружницата ќе се определи доведуваки ги параметарските равенки во облик

$\begin{array}{}x-2=5\text{cos}t\\ y+3=5\text{sin}t\end{array}$

и ако по квадрирање на двете равенки

$\begin{array}{}(x-2{)}^2=\text{25}{\text{cos}}^{2}t\\ (y+3{)}^2=\text{25}{\text{sin}}^{2}t\end{array}$

ги собереме се добива

$(x-2{)}^2+(y+3{)}^2=\text{25}({\text{cos}}^{2}t+{\text{sin}}^{2}t)$ ,

односно

$(x-2{)}^2+(y+3{)}^2=5^2$ ,

што претставува централна равенка на кружница со центар во точката $S(\mathrm{2,}-3)$ и радиус $r=5$ .

Пример 1.

Кривата што ја опишува точка од кружница со радиус $a$ која се тркала по $x-$ оската се нарекува циклоида (Сл. 2.3.) и е зададена со параметарските равенки

$\begin{array}{}x=a(t-\text{sin}t)\\ y=a(1-\text{cos}t)\text{.}\end{array}$

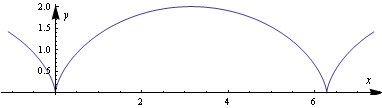Слика 2.3 Циклоида

Пример 2.

Равенката на кривата во правоаголни координати

$x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$

се нарекува астроида и често пати се проучува и во параметарски облик преку нејзините параметарски равенки

$\begin{array}{}x=a{\text{cos}}^{3}t\\ y=a{\text{sin}}^{3}t\text{.}\end{array}$

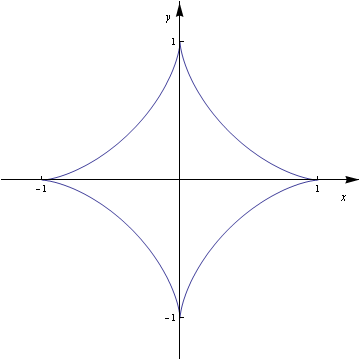Слика 2.4 Астроида

Графикот на астроидата (Сл. 2. 4) е крива која ја опишува точка од кружница со радиус $a/4$ која се тркала по внатрешната страна од кружница со радиус $a$ .