| << Chapter < Page | Chapter >> Page > |
In this chapter, you will learn to:
Application problems in business, economics, and social and life sciences often ask us to make decisions on the basis of certain conditions. These conditions or constraints often take the form of inequalities. In this section, we will look at such problems.
A typical linear programming problem consists of finding an extreme value of a linear function subject to certain constraints. We are either trying to maximize or minimize our function. That is why these linear programming problems are classified as maximization or minimization problems , or just optimization problems . The function we are trying to optimize is called an objective function , and the conditions that must be satisfied are called constraints . In this chapter, we will do problems that involve only two variables, and therefore, can be solved by graphing. We begin by solving a maximization problem.
Niki holds two part-time jobs, Job I and Job II. She never wants to work more than a total of 12 hours a week. She has determined that for every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation. If she makes $40 an hour at Job I, and $30 an hour at Job II, how many hours should she work per week at each job to maximize her income?
We start by choosing our variables.
Let
and
Now we write the objective function. Since Niki gets paid $40 an hour at Job I, and $30 an hour at Job II, her total income I is given by the following equation.
Our next task is to find the constraints. The second sentence in the problem states, "She never wants to work more than a total of 12 hours a week." This translates into the following constraint:
The third sentence states, "For every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation." The translation follows.
The fact that and can never be negative is represented by the following two constraints:
, and .
Well, good news! We have formulated the problem. We restate it as
Maximize
Subject to:
In order to solve the problem, we graph the constraints as follows.
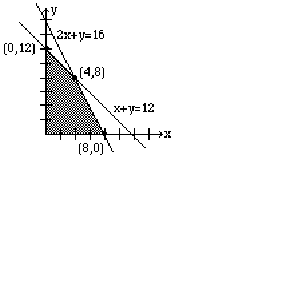
Observe that we have shaded the region where all conditions are satisfied. This region is called the feasibility region or the feasibility polygon.
The Fundamental Theorem of Linear Programming states that the maximum (or minimum) value of the objective function always takes place at the vertices of the feasibility region.
Therefore, we will identify all the vertices of the feasibility region. We call these points critical points. They are listed as (0, 0), (0, 12), (4, 8), (8, 0). To maximize Niki's income, we will substitute these points in the objective function to see which point gives us the highest income per week. We list the results below.
| Critical Points | Income |
| (0,0) | |
| (0.12) | |
| (4,8) | |
| (8,0) |
Clearly, the point (4, 8) gives the most profit: $400.
Therefore, we conclude that Niki should work 4 hours at Job I, and 8 hours at Job II.

Notification Switch
Would you like to follow the 'Applied finite mathematics' conversation and receive update notifications?