| << Chapter < Page | Chapter >> Page > |
This module is intended to illustrate concepts related to the solution of engineering problems using straight lines. It has formed the basis of a Laboratory session associated with a MATH 1508 (Precalculus) course taught at the University of Texas at El Paso. The examples contained herein are drawn from the fields of fluid mechanics, mechanics, and electric circuits. Exercises are included at the end of this module.
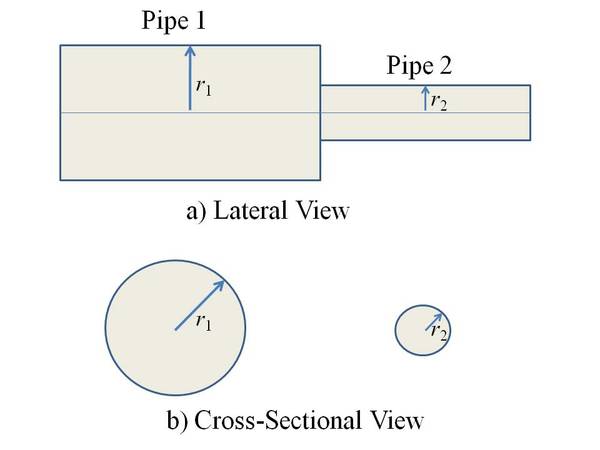
Figure 1 illustrates a piping system that consists of two pipes. Pipe1 has a radius of r 1 while the radius of Pipe 2 is r 2 . These two pipes are joined so that water can pass from the left to the right.
Quite some time ago, engineers observed that the velocity of a fluid in Pipe 1 ( v 1 ) for such a system would be quite a bit lower in value than the velocity of the fluid in Pipe 2 ( v 2 ). As a consequence, engineers sought a means for determining the relationship between the velocity of fluids in the two pipes that comprise this sort of system.
Their solution to the problem of determining the relationship between the two velocities ( v 1 and v 2 ) is provided by a very important principle in fluid mechanics that is called the continuity equation . The continuity equation states
where A 1 represents the cross-sectional area of Pipe 1 and A 2 represents the cross-sectional area of Pipe 2. For the continuity equation to be valid it is important to recognize that the flow of water be continuous as it passes from the first to the second pipe.
By rearranging terms in equation (1), we can formulate an equivalent expression that may be a bit more insightful
Thus we can conclude that the ratio of the area of the two pipes provides a multiplicative constant relating the velocities of the fluid in the two pipes.
We recall that the equation for a straight line takes the form
Equation (4) indicates that there is a linear (straight line) relationship between the velocity ( v 2 ) of the fluid in the second pipe and the velocity ( v 1 ) of the fluid in the first pipe. If we establish v 1 as the independent variable, then the dependent variable v 2 is defined as a linear function of v 1 . The slope ( m ) of the line is the ratio of the cross-sectional areas , while the y-intercept ( b ) is zero.
Let us now apply our knowledge of the continuity equation to a problem.
Question: Suppose that the radius of Pipe 1 is 4.00 cm and the radius of Pipe 2 is 2.50 cm. The velocity of the water in Pipe 1 is measured to be 3.00 m/sec. Find the velocity of the water in Pipe 2.
Solution: We begin our solution by establishing the cross-sectional areas of each pipe. Because the cross-sectional profile of each pipe is a circle, we may compute the two cross-sectional areas using the formula for the area of a circle:

Notification Switch
Would you like to follow the 'Math 1508 (laboratory) engineering applications of precalculus' conversation and receive update notifications?