| << Chapter < Page | Chapter >> Page > |
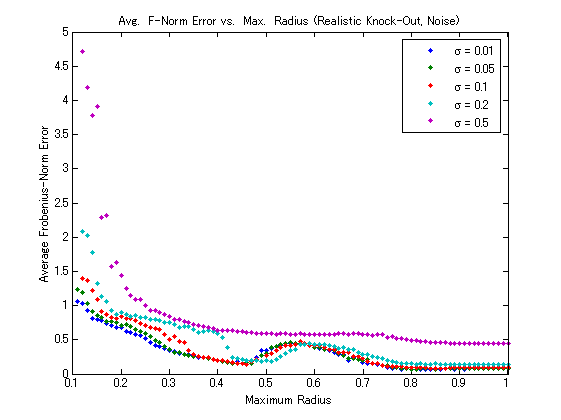
The figures below, which show the results for the realistic knock-out trials, are similar to those above except that they plot the average relative Frobenius-norm error over 25 trials versus maximum radius as opposed to fraction of unknown entries.
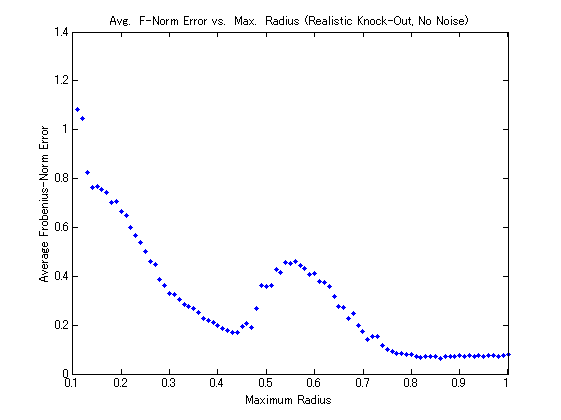
The most salient feature of these graphs is the odd “hump" that appears from radius values of about 0.5 to 0.7, even in the no-noise case. Over this range, despite the fact that the radius is growing (meaning that more pairwise distances are known), the error in the completed matrix is actually becoming worse rather than better, which seems to contradict the excellent results discussed above for the random knock-out case. At the time of this writing, we are still unsure as to why this “hump" appears; however, we suspect that it may have something to do with the OptSpace algorithm itself because when we run the same experiment using the SVT algorithm of Candès, the hump doesnot appear, as the figure below shows. (Note that, nevertheless, OptSpace tends to produce less error than SVT, even over the offending range of radii.)
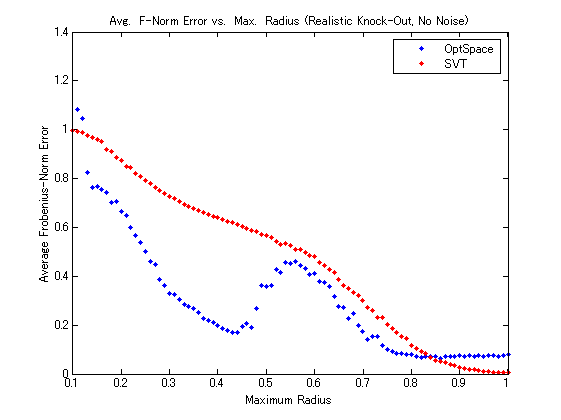
Perhaps more important than the “hump," however, is the fact that the scales on the axes of the above graphs alone are enough to demonstrate that the performance of the method in the realistic knock-out case is decidedly worse than that for the random knock-out case. For example, consider the figure below, which shows the results of a typical no-noise, realistick knock-out trial with a maximum radius of 1. For this particular trial, over 97 percent of the pairs are known. The reconstructed network matches the original quite well near the “center" of the network, but at the edges, the match becomes much worse. This behavior is not exhibited at all by random knock-out trials forcomparable fractions of unknown entries, as the picture at the bottom of the figure illustrates, which was generated from a non-noise random knock-out trial in which 90 percent of the pairs were known.
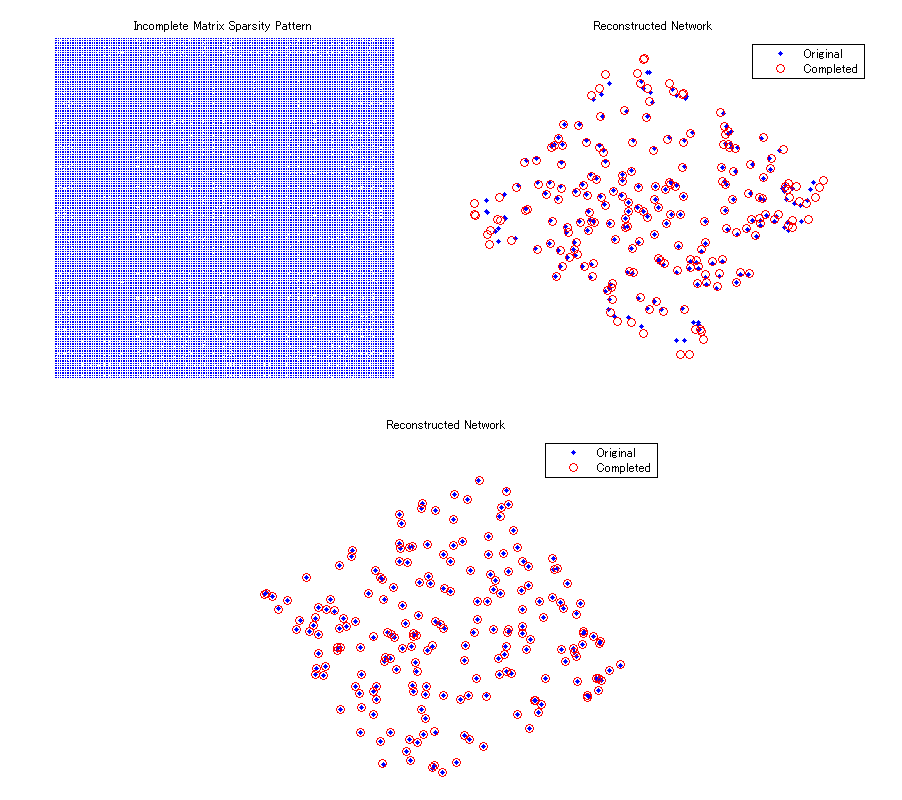
Shrinking the radius only makes matters worse, as the next figure illustrates. The maximum radius here is . Around 77 percent of the distance pairs are known, and yet the match is terrible.

Adding noise only makes the results even worse. At first glance, this behavior appears to be inexplicable; however examining the sparsity patterns of the incomplete matrices reveals an interesting fact: the entry knock-out in the realistic case is far from being “random!" The sparsity patterns for the realistic knock-out matrices reveal clear patterns of lines in their knocked-out entries that are not present in those for random knock-out cases. This unintendedregularity of entry selection violates the assumption made in all of the matrix completion literature that the known entries are taken from a uniform sampling of the matrix, so it would seem that none of the theoretical results that have been derived apply in this case.
Our results show that matrix completion presents a viable means of approaching the sensor network localization problem under the assumption that the known pairs of distances come from a uniform sampling of the distance matrix. Under these conditions, matrix completion provides excellent network reconstruction and is fairly robust to noise. Unfortunately, its performance in the more realistic case in which distance information will be excluded or included basedon a maximum possible distance over which two sensors can communicate leaves much to be desired.
With more time on this project, we would like to have explored the following questions further:

Notification Switch
Would you like to follow the 'A matrix completion approach to sensor network localization' conversation and receive update notifications?