0.3 Low-dimensional signal models  (Page 18/3)

We now survey some common and important models in signal processing, each of which involves some notion of conciseness tothe signal structure. We see in each case that this conciseness gives rise to a low-dimensional geometry within the ambient signalspace.

Linear models

Some of the simplest models in signal processing correspond to linear subspaces of the ambient signal space. Bandlimited signals are one such example. Supposing, for example,that a $2\pi$ -periodic signal $f$ has Fourier transform $F\left(\omega \right)=0$ for $\left|\omega \right|>B$ , the Shannon/Nyquist sampling theorem  [link] states that such signals can be reconstructed from $2B$ samples. Because the space of $B$ -bandlimited signals is closed under addition and scalar multiplication, it follows that the set of such signals forms a $2B$ -dimensional linear subspace of $L^2\left([0,2\pi )\right)$ .

Linear signal models also appear in cases where a model dictates a linear constraint on a signal. Considering a discrete length- $N$ signal $x$ , for example, such a constraint can be written in matrix form as

A very similar class of models concerns signals living in an affine space, which can be represented for a discrete signal using

Revisiting the dictionary setting (see Signal Dictionaries and Representations ), one last important linear model arises in cases where we select $K$ specific elements from the dictionary $\Psi$ and then construct signals using linear combinations of only these $K$ elements; in this case the set of possible signals forms a $K$ -dimensional hyperplane in the ambient signal space (see [link] (a)).

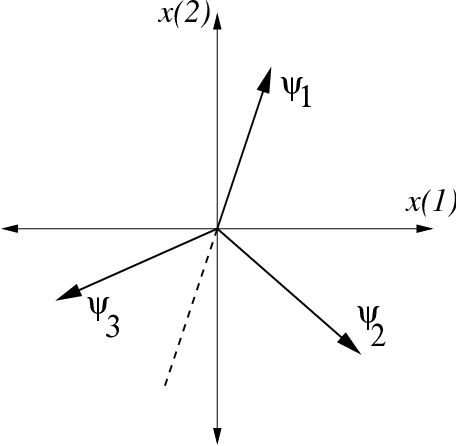
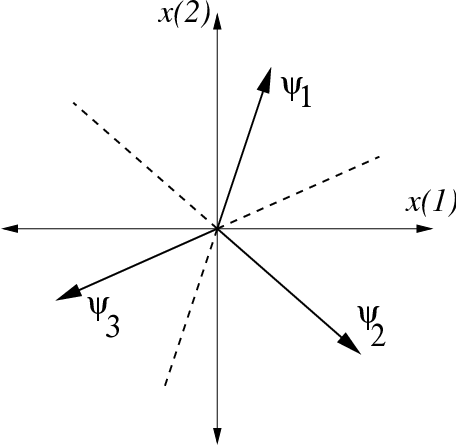
For example, we may construct low-frequency signals using combinations of only the lowest frequency sinusoids from theFourier dictionary. Similar subsets may be chosen from the wavelet dictionary; in particular, one may choose only elements that spana particular scaling space $V_j$ . As we have mentioned previously, harmonic dictionaries such as sinusoids and wavelets arewell-suited to representing smooth Lipschitz smoothness We say a continuous-time function of $D$ variables has smoothness of order $H>0$ , where $H=r+\nu$ , $r$ is an integer, and $\nu \in (0,1]$ , if the following criteria are met [link] , [link] :

• All iterated partial derivatives with respect to the $D$ directions up to order $r$ exist and are continuous.
• All such partial derivatives of order $r$ satisfy a Lipschitz condition of order $\nu$ (also known as a Hölder condition).(A function $d\in \text{Lip}\left(\nu \right)$ if $|d(t_1+t_2)-d\left(t_1\right)|\le C\parallel t_2{\parallel }^{\nu }$ for all $D$ -dimensional vectors $t_1,t_2$ .)