1. Home
  2. Math 1508 (laboratory) engineering
  3. Math 1508 (laboratory) engineering
  4. Exponents

0.3 Exponents  (Page 3/4)

<< Chapter < Page
  Math 1508 (laboratory) engineering     Page 3 / 4
Chapter >> Page >

We can obtain an alternative form for the power absorbed by the resistor. We begin with the general expression for the power absorbed by a resistor

P R = I × V size 12{P rSub { size 8{R} } =I times V} {}

If we now substitute the expression for V provided by Ohm’s Law into this equation, we obtain an alternative expression for power

P R = I ⋅ ( I × R ) size 12{P rSub { size 8{R} } =I cdot \( I times R \) } {}
P R = I 2 R size 12{P rSub { size 8{R} } =I rSup { size 8{2} } R} {}

This relationship expresses the electrical power absorbed by the resistor as a product of the square of the current by the resistance.

Thus we have two equally useful formulas for the computation of the power absorbed by a resistor. One involves the square of the voltage, while the other incorporates the square of the current. Each formula involves a term that is raised to an exponent of 2.

Example (Electrical Power)

A 9 Volt battery is connected to a single 10 kΩ resistor.

Electric circuit.

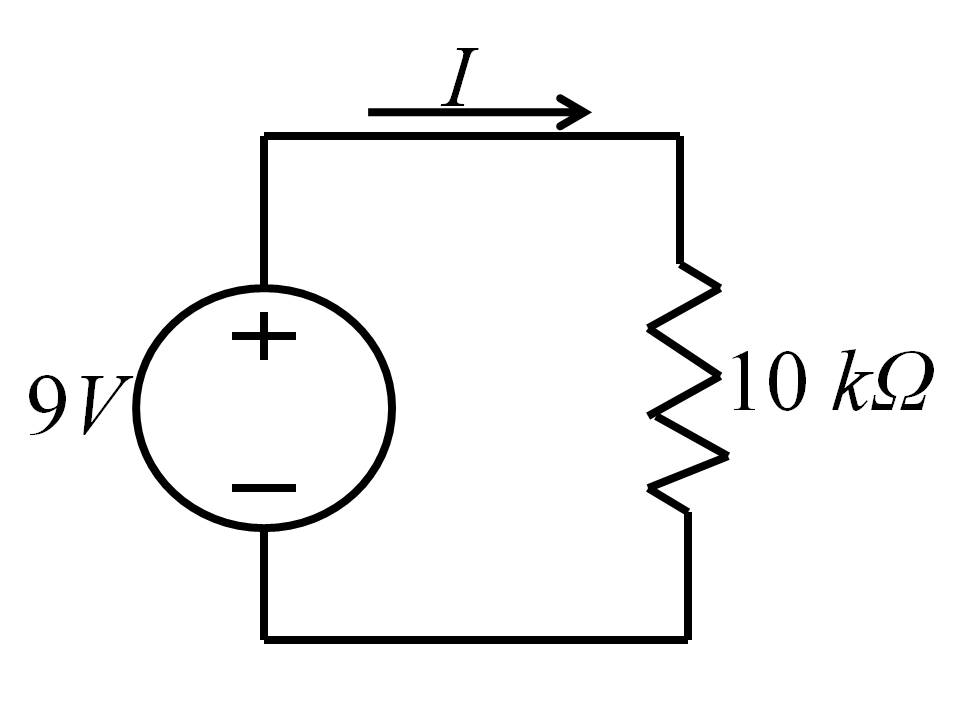
Question : How much power is dissipated in the resistor? (Express the result in engineering notation.)

P R = ( 9 V ) 2 10 × 10 3 Ω size 12{P rSub { size 8{R} } = { { \( 9`V \) rSup { size 8{2} } } over {"10"` times "10" rSup { size 8{3} } %OMEGA } } } {}
P R = 81 V 2 10 4 Ω size 12{P rSub { size 8{R} } = { {"81"``V rSup { size 8{2} } } over {"10" rSup { size 8{4} } ` %OMEGA } } } {}
P R = 81 × 10 − 4 V 2 Ω size 12{P rSub { size 8{R} } ="81" times "10" rSup { size 8{ - 4} } left ( { {V rSup { size 8{2} } } over { %OMEGA } } right )} {}
P R = 81 × ( 10 − 1 × 10 − 3 ) W size 12{P rSub { size 8{R} } ="81" times \( "10" rSup { size 8{ - 1} } times "10" rSup { size 8{ - 3} } \) `W} {}
P R = ( 81 × 10 − 1 ) × 10 − 3 W size 12{P rSub { size 8{R} } = \( "81" times "10" rSup { size 8{ - 1} } \) times "10" rSup { size 8{ - 3} } `W} {}
P R = 8 . 1 × 10 − 3 W size 12{P rSub { size 8{R} } =8 "." 1 times "10" rSup { size 8{ - 3} } `W} {}
P R = 8 . 1 mW size 12{P rSub { size 8{R} } =8 "." 1` ital "mW"} {}

Gravitational force

Every object of finite mass near the surface of the earth experiences a force that pulls it downward. This force is called weight. In the 17 th Century, Sir Isaac Newton postulated that this force which attracts objects to the earth might well be a particular example of a more general kind of interaction between objects. Newton was engaged in the study of the motion of planets around the sun and felt that the planets should obey the same laws of motion as objects falling toward the earth due to their weight. In one of humankind’s greatest bits of insight, Newton discovered that the forces responsible for both planetary motion and the phenomenon of weight could be equally understood if one hypothesized that every object of finite mass attracts every other object of finite mass with a force that depends upon the individual masses of the objects. Such forces are known as gravitational forces and they serve as a basis for what is now known as Newton’s law of gravitation .

Let us consider two objects of respective masses m 1 an m 2 that are separated by a distance that we denote as r . Newton’s law of gravitation states that each object will exert on the other an attractive force, directed along a straight line connecting the two objects. The magnitude of the force that mass m 1 exerts on m 2 is equal to the magnitude of the force that m 2 exerts on m 1 . The magnitude of the force that the first mass exerts on the second is provided by the equation

F = G m 1 m 2 r 2 . size 12{F=G` { {m rSub { size 8{1} } `m rSub { size 8{2} } } over {r rSup { size 8{2} } } } ` "." } {}

Here, G represents the universal gravitational constant and is given by

G = 6 . 67 × 10 − 11 N − m 2 / kg 2 . size 12{G=6 "." "67"` times `"10" rSup { size 8{ - "11"} } `N - m rSup { size 8{2} } / ital "kg" rSup { size 8{2} } ` "." } {}

Because the universal constant is so small, the gravitational forces that exists between objects of ordinary mass are extremely small.

We can incorporate the value for G along with the use of exponents in the equation for the magnitude of the force to yield the expression that follows.

F = ( 6 . 67 × 10 − 11 Newton − meter 2 / kg 2 ) ( m 1 m 2 ) r − 2 size 12{F= \( 6 "." "67"` times `"10" rSup { size 8{ - "11"} } ` ital "Newton" - ital "meter" rSup { size 8{2} } / ital "kg" rSup { size 8{2} } \) ` \( m rSub { size 8{1} } `m rSub { size 8{2} } \) `r rSup { size 8{ - 2} } } {}

Thus we can see that exponents play an important role in the formulation of Newton’s law of gravitation. Exponents are important to the expression of the universal gravitational constant and the attractive force between two objects depends upon the reciprocal of the square of the distance between the objects.
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Math 1508 (laboratory) engineering applications of precalculus. OpenStax CNX. Aug 24, 2011 Download for free at http://cnx.org/content/col11337/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Math 1508 (laboratory) engineering applications of precalculus' conversation and receive update notifications?

Ask