| << Chapter < Page | Chapter >> Page > |
where and are the momenta of cars 1 and 2 after the collision. (We often use primes to denote the final state.)
This result—that momentum is conserved—has validity far beyond the preceding one-dimensional case. It can be similarly shown that total momentum is conserved for any isolated system, with any number of objects in it. In equation form, the conservation of momentum principle for an isolated system is written
or
where is the total momentum (the sum of the momenta of the individual objects in the system) and is the total momentum some time later. (The total momentum can be shown to be the momentum of the center of mass of the system.) An isolated system is defined to be one for which the net external force is zero
An isolated system is defined to be one for which the net external force is zero
Perhaps an easier way to see that momentum is conserved for an isolated system is to consider Newton’s second law in terms of momentum, . For an isolated system, ; thus, , and is constant.
We have noted that the three length dimensions in nature— , , and —are independent, and it is interesting to note that momentum can be conserved in different ways along each dimension. For example, during projectile motion and where air resistance is negligible, momentum is conserved in the horizontal direction because horizontal forces are zero and momentum is unchanged. But along the vertical direction, the net vertical force is not zero and the momentum of the projectile is not conserved. (See [link] .) However, if the momentum of the projectile-Earth system is considered in the vertical direction, we find that the total momentum is conserved.
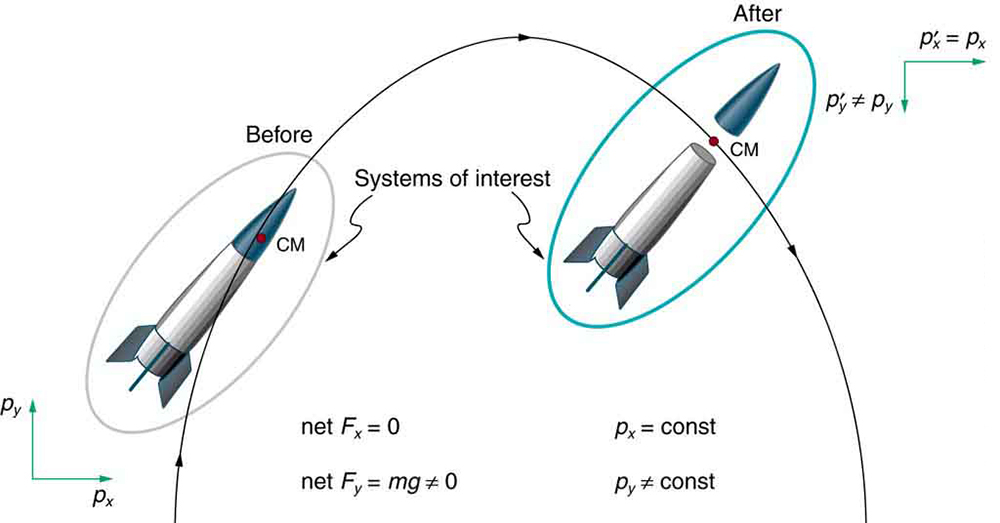
The conservation of momentum principle can be applied to systems as different as a comet striking Earth and a gas containing huge numbers of atoms and molecules. Conservation of momentum is violated only when the net external force is not zero. But another larger system can always be considered in which momentum is conserved by simply including the source of the external force. For example, in the collision of two cars considered above, the two-car system conserves momentum while each one-car system does not.
The conservation of momentum principle not only applies to the macroscopic objects, it is also essential to our explorations of atomic and subatomic particles. Giant machines hurl subatomic particles at one another, and researchers evaluate the results by assuming conservation of momentum (among other things).
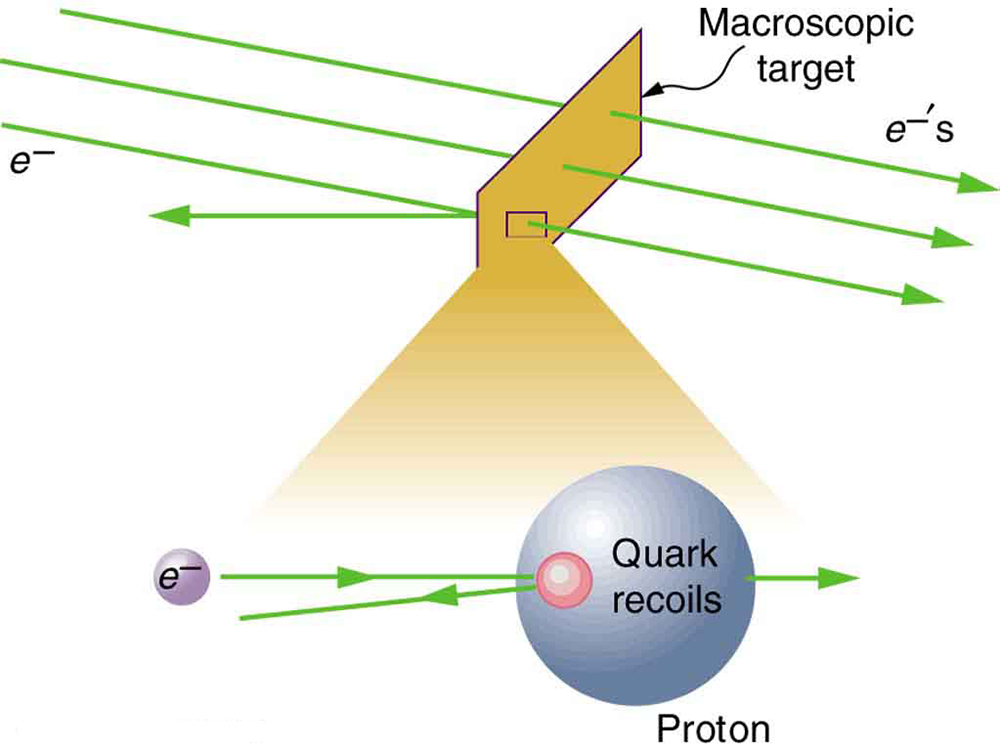
On the small scale, we find that particles and their properties are invisible to the naked eye but can be measured with our instruments, and models of these subatomic particles can be constructed to describe the results. Momentum is found to be a property of all subatomic particles including massless particles such as photons that compose light. Momentum being a property of particles hints that momentum may have an identity beyond the description of an object’s mass multiplied by the object’s velocity. Indeed, momentum relates to wave properties and plays a fundamental role in what measurements are taken and how we take these measurements. Furthermore, we find that the conservation of momentum principle is valid when considering systems of particles. We use this principle to analyze the masses and other properties of previously undetected particles, such as the nucleus of an atom and the existence of quarks that make up particles of nuclei. [link] below illustrates how a particle scattering backward from another implies that its target is massive and dense. Experiments seeking evidence that quarks make up protons (one type of particle that makes up nuclei) scattered high-energy electrons off of protons (nuclei of hydrogen atoms). Electrons occasionally scattered straight backward in a manner that implied a very small and very dense particle makes up the proton—this observation is considered nearly direct evidence of quarks. The analysis was based partly on the same conservation of momentum principle that works so well on the large scale.
Can objects in a system have momentum while the momentum of the system is zero? Explain your answer.
Must the total energy of a system be conserved whenever its momentum is conserved? Explain why or why not.
Professional Application
Train cars are coupled together by being bumped into one another. Suppose two loaded train cars are moving toward one another, the first having a mass of 150,000 kg and a velocity of 0.300 m/s, and the second having a mass of 110,000 kg and a velocity of . (The minus indicates direction of motion.) What is their final velocity?
0.122 m/s
Suppose a clay model of a koala bear has a mass of 0.200 kg and slides on ice at a speed of 0.750 m/s. It runs into another clay model, which is initially motionless and has a mass of 0.350 kg. Both being soft clay, they naturally stick together. What is their final velocity?
Professional Application
Consider the following question: A car moving at 10 m/s crashes into a tree and stops in 0.26 s. Calculate the force the seatbelt exerts on a passenger in the car to bring him to a halt. The mass of the passenger is 70 kg. Would the answer to this question be different if the car with the 70-kg passenger had collided with a car that has a mass equal to and is traveling in the opposite direction and at the same speed? Explain your answer.
In acollision withan identicalcar, momentumis conserved.Afterwards for bothcars. Thechange inmomentum willbe thesame asin thecrash withthe tree.However, theforce onthe bodyis notdetermined sincethe timeis notknown. Apadded stopwill reduceinjurious forceon body.

Notification Switch
Would you like to follow the 'Unit 6 - momentum' conversation and receive update notifications?