0.2 Steering vector

The steering vector

The steering vector _­­­ e represents the set of phase delays experienced by a plane wave as it reaches each element in an array of sensors. The mathematical representation of it is

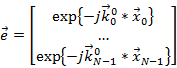
Where j is the imaginary unit, k ­ _n is the wave number at the n th sensor, and x­ _n is the position vector of the n th sensor in ( x , y , z ) coordinates. If the sensor array is two-dimensional, all z coordinates can be treated as 0 and omitted from the position vector in calculations. The wave number of a plane wave is its spatial frequency, or how many waves exist over a specified distance. It is a function of the frequency of the propagating wave, the material through which it is travelling, and its original location or direction of propagation. For our specific application, we actually use the angular wave number, which is written as (2π/λ) and indicates the number of wavelengths per 2π unit distance.

The role of the steering vector e in beamforming is to define the assumed propagation direction of the source’s signal. In other words, it is the part of the beamforming process that chooses the direction in which the sensor array creates an output beam. Because e is designed to cancel the phase shifts at each sensor in the array and the wave number k must, by definition, assume a propagation direction, the steering vector has the effect of moving the each sensor’s output to a particular direction, thus focusing the beam.