Се прикажува вектор во простор и операции со вектори преку нивните координати.
Правоаголни координати на вектор
Векторот
во тродимензионален простор чиј почеток е во координатниот почеток
О (0, 0, 0), а крајот во точката
А (
x ,
y
,
z ), аналитички се означува со
= {
x ,
y ,
z }.
Реалните броеви
x ,
y и
z се нарекуваат координати на векторот
(Сл. 1.6.)
Нула векторот има координати
= {0, 0, 0}.
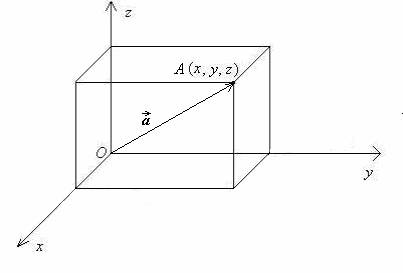 |
| Слика 1.6. Вектор во простор |
Понатаму следат операциите со векторите дефинирани аналитички, т.е. преку нивните координати.
Еднаквост на вектори
Векторите
= {
x
1
,
y
1
,
z
1 } и
= {
x
2
,
y
2
,
z
2 } се еднакви ако им се еднакви соодветните координати, т.е.
x
1 =
x
2 ,
y
1 =
y
2 ,
z
1 =
z
2 .
Сума, разлика и множење на вектор со скалар
За векторите
= {
x
1
,
y
1
,
z
1 } и
= {
x
2
,
y
2
,
z
2 } се дефинираат претходно воведените основни операции со вектори, но сега преку нивните координати:
= {
x
1 +
x
2 ,
y
1 +
y
2 ,
z
1 +
z
2 }
= {
x
1 -
x
2 ,
y
1 -
y
2 ,
z
1 -
z
2 }
λ
= λ{
x
1
,
y
1
,
z
1 } = {λ
x
1
, λ
y
1
, λ
z
1 }.
Пример 1. Ако
= {5, -2, 7} и
= {0, 3, -1}, тогаш
= {5+0, -2 +3, 7-1} = {5, 1, 6}
= {5-0, -2 -3, 7- (-1)} = {5, -5, 8}
- 3
= -3{0, 3, -1} = {0, -9, 3}
= 2{5, -2, 7} + 4{0, 3, -1} =
= {10, -4, 14} + {0, 12, -4} = {10, 8, 10}. ◄
Колинерни вектори
Векторите
= {
x
1
,
y
1
,
z
1 } и
= {
x
2
,
y
2
,
z
2 } се колинерни ако
, (
λ ≠ 0), односно ако важи
.
Пример 2. Векторите
= {2, 3, - 5} и
= {- 6, - 9, 15} се колинерни бидејќи
. ◄
Закони на векторската алгебра
Нека
,
и
се вектори, а
λ
и
μ скалари, тогаш важат следните закони:
(комутативен закон за собирање на вектори);
(асоцијативен закон за собирање на вектори);
(асоцијативен закон за множење со скалар);
(дистрибутивен закон);
(дистрибутивен закон).
Координати на вектор меѓу две точки
Векторот
за кој точката
А (
x
1
,
y
1
,
z
1 ) е почетна а
B (
x
2
,
y
2
,
z
2 ) крајна точка, е определен со следните координати
= {
x
2 -
x
1 ,
y
2 -
y
1 ,
z
2 -
z
1 }.
Пример 3. Да се определат координатите на векторот
за кој
А (2, 4, -3) е почетна, а
B (0, -1, 12) крајна точка.
Решение.
= {0
- 2, -1 -4, 12
- (-3)} = {-2, -5, 15}. ◄
Пример 4. Да се определат координатите на крајната точка
B на векторот
= {2, 3, - 5}, ако
А (1, 0, - 2) е почетна точка.
Решение. Векторот
со почеток во точката
А (1, 0, - 2) и крај во
B (
x ,
y ,
z ) ќе има координати
= {
x - 1,
y - 0,
z
- (-2)}.
Бидејќи координатите на векторот
се дадени, од условот за еднаквост на векторите ќе следи
{
x - 1,
y - 0,
z
- (-2)} = {2, 3, - 5}
од каде
x - 1 = 2
x = 3,
y - 0 = 3
y = 3,
z
+ 2 = - 5
z = - 7.
Значи, бараната крајна точка на векторот е
B (3, 3, - 7). ◄
Интензитет на вектор
Интензитетот на векторот
= {
x
,
y
,
z } зададен преку неговите координати, се определува со
.
Пример 5. Да се определи итензитетот на векторот
ако
= {-2, 3, 2},
= {5, 0, - 1}.
Решение. Векторот
е со координати
= {-2, 3, 2} + 2{5, 0, - 1} = {-2 + 10, 3 + 0, 2 -2} = {8, 3, 0}
и со интензитет
. ◄
Пример 6. Да се определи единичниот вектор
за векторот
= {-2, 3, 2}.
Решение.
= {-2, 3, 2}/
= {- 2/
, 3/
, 2/
}. ◄
Единични вектори на кординатните оски
На координатните оски се определуваат единични вектори и тоа:
на
x - оската единичен вектор
= {1, 0, 0},
на
y - оската единичен вектор
= {0, 1, 0},
на
z - оската единичен вектор
= {0, 0, 1}.
Овие три единични вектори се линерано независни, што значи дека ниту еден од нив не може да се претстави како линерна комбинација од останатите два вектора и затоа нивната линерна комбинација
+
+
=
e можна само за
.
Секој вектор
= {
x
,
y
,
z } во простор може да се напише како линерна комбинација од единичните вектори
=
x
+
y
+
z
,
бидејќи
= {
x ,
y ,
z } = {
x ,
0, 0} + {0,
y ,
0} + {0,
0,
z } =
=
x {1, 0, 0} +
y {0, 1, 0} +
z {0, 0, 1} =
x
+
y
+
z
.
Затоа векторот
= {-2, 3, 2} разложен по единичните вектори од координатните оски е
= {-2, 3, 2} = - 2
+ 3
+ 2
.
Пример 7. Да се покаже дека векторите
= {1, -1, 2},
= {1, 2, -1} и
= {3, 1, 1} се линерно независни.
Решение. Трите вектори
,
и
се линерано независни ако линеарната комбинација
+
+
=
е можна само за
.
Поаѓајќи од равенството за линерна комбинација на векторите
{1, -1, 2} +
{1, 2, -1} +
{3, 1, 1} =
се добива
{
+
+ 3
, -
+ 2
+
, 2
-
+
} =
,
а ова векторско равенство се сведува на хомоген систем од три линеарни равенки со три непознати
+
+ 3
= 0
-
+ 2
+
= 0
2
-
+
= 0.
Детерминантата на системот D = 3 ≠ 0, од каде следува дека системот има едно единствено решение и тоа е тривијалното решение
. Значи, трите вектори се линеарно независни. ◄
Пример 8. Да се претстави векторот
= {-1, 1, 5} како линеарна комбинација од векторите
= {1, 0, 1},
= {3, 2, 0} и
= {0, 1, 1}.
Решение. За претставување (разложување) на векторот
преку векторите
,
и
се поаѓа од релацијата за линеарна комбинација
во која треба да се определат константите
α ,
β
и
γ . Запишувајки ја горната релација со вектори преку нивните координати се добива
{-1, 1, 5} =
α {1, 0, 1} +
β {3, 2, 0} +
γ {0, 1, 1}
односно
{-1, 1, 5} = {
α + 3
β + 0
γ , 0
α
+ 2
β +
γ ,
α + 0
β +
γ },
и од еднаквоста на векторите се добива нехомогениот систем равенки
чии решенија се
α = 2,
β
= -1,
γ = 3. Тоа значи дека векторот
може да се запише како линерна комбинација од векторите
,
и
со изразот
. ◄

