| << Chapter < Page | Chapter >> Page > |
Imagine the data we have is a linear mixture of unknown latent factors and the factors are mutually independent and non-Gaussian, our goal is to find the underlying structure and identify these components. As shown before, PCA assumes Gaussianity. The condition and imply independence only when the data is Gaussian. ICA corrects this by looking for maximally independent components (rather than uncorrelated) ones. We know that uncorrlation is characterized by: while independence is given by The independence is stronger than uncorrelation because it measures the existence of any relationship. On the other hand, uncorrlation only measures linear relationship. Model for ICA looks like this:
where A is the mixing matrix and S is the source signals (rows of S independent) and we recover the signal using the “whitening” matrix W, where:
Popular algorithms do this by maximizing its distance from Gaussian using either entropy or neg-entropy (Gaussian has maximal entropy) – they are solved using quasi-Newton scheme. In addition to this, some often used contrast functions to Gaussian include 3rd moment skewness, 4th moment kurtosis (kurtosis is zero for a Gaussian random variable) and sigmoidal. We used FastICA. It’s efficient and converges quickly.
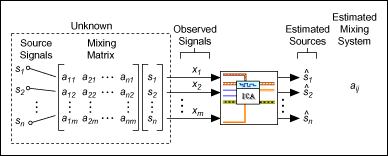 (Figure Credit: http://zone.ni.com/reference/en-XX/help/372656B-01/lvasptconcepts/tsa_multivariate_stat_analysis/)
(Figure Credit: http://zone.ni.com/reference/en-XX/help/372656B-01/lvasptconcepts/tsa_multivariate_stat_analysis/)

Notification Switch
Would you like to follow the 'Comparison of three different matrix factorization techniques for unsupervised machine learning' conversation and receive update notifications?