| << Chapter < Page | Chapter >> Page > |
Two intuitively reasonable approaches to developing the equations for the FDM-TDM transmultiplexer are presented in this section. The first emulates [link] . We first develop the equations for a digital counterpart of the analog tuners used in the filter bank and then observe that significant computational improvements can be obtained when the tuning frequencies are linked together in a simple way. The second subsection starts from a different point, that of using the discrete Fourier transform as a spectral channelizer. We ultimately find out that these two approaches yield essentially the same analytical results.
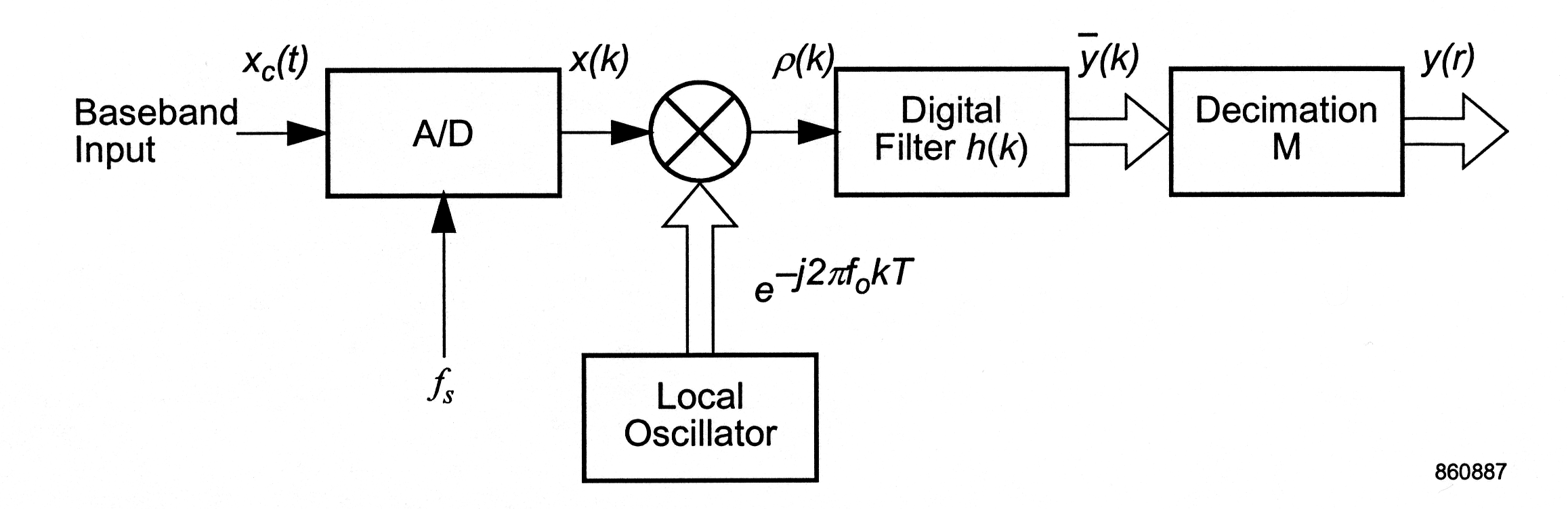
The input FDM signal is assumed to be the continuous-time waveform . The analog-to-digital converter shown in [link] samples this waveform at the uniform rate of f s samples per second, producing the discrete-time sequence , where , the integer k is the time index, and T is the sampling interval given by . The spectrum of this sequence is shifted down in frequency by multiplying it by a complex exponential of the form , where f 0 is the desired amount of the frequency downconversion. The product of and this exponential is then filtered in discrete time by using the pulse response . The duration of the pulse response is assumed to be finite and in particular of length no greater than L , an integer. The filter output is then decimated by a factor of M , yielding the sequence , where the integer r is the decimated time index.
These processing steps are shown in graphical form in [link] . Both sides of the two-sided spectrum of the sampled input signal are seen in [link] (a). For the moment, the input signal is assumed to be real-valued and therefore the spectrum is symmetrical around 0 Hz Even though real-valued inputs are assumed here, all of the ensuing analysis applies to complex-valued signals as well. . A channel of interest in this spectrum has been shaded and its center frequency is noted to be f 0 . Multiplying the input signal by has the effect of shifting the spectrum to the left (assuming ) and centering the desired channel at 0 Hz. The downconverted signal is now complex-valued, and therefore spectral symmetry around 0 Hz is neither required nor expected. The transfer function of the lowpass filter appears in [link] (c). The filter pulse response is chosen to attain the desired spectral characteristics. In particular, the filter needs to pass the channel of interest without degradation and suppress all others sufficiently. How to design such a pulse response is discussed in Appendix A. In general, the quality of the filter grows with the value of the parameter L . The filter shown here is symmetrical around 0 Hz and its pulse response can therefore be real-valued. This is not required however.
After the application of the shifted signal to the filter, the spectrum shown in [link] (d) results. The desired channel is isolated from all others. It is sampled, however, at a rate far faster than required by the Nyquist sampling theorem. The filter output is then decimated by the factor M , resulting in the spectrum shown in [link] (e). The channel's bandwidth is the same as before but now its percentage bandwidth, that is, its bandwidth compared to its final sampling rate, is much higher. In a good digital tuner the percentage bandwidth after decimation usually ranges between 0.5 and 0.9, where unity is the theoretical limit imposed by the sampling theorem.

Notification Switch
Would you like to follow the 'An introduction to the fdm-tdm digital transmultiplexer' conversation and receive update notifications?