| << Chapter < Page | Chapter >> Page > |
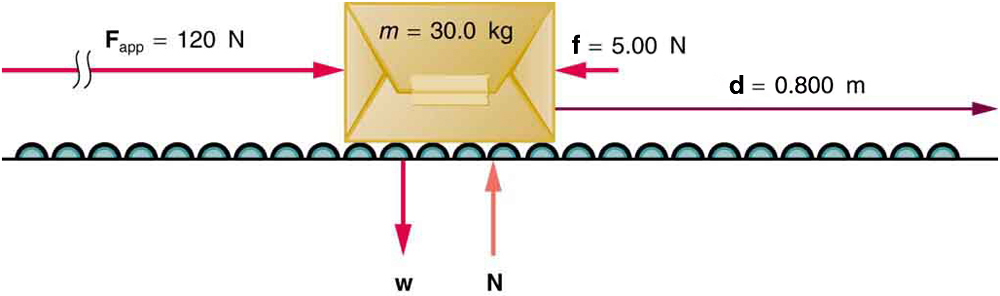
The force of gravity and the normal force acting on the package are perpendicular to the displacement and do no work. Moreover, they are also equal in magnitude and opposite in direction so they cancel in calculating the net force. The net force arises solely from the horizontal applied force and the horizontal friction force . Thus, as expected, the net force is parallel to the displacement, so that and , and the net work is given by
The effect of the net force is to accelerate the package from to . The kinetic energy of the package increases, indicating that the net work done on the system is positive. (See [link] .) By using Newton’s second law, and doing some algebra, we can reach an interesting conclusion. Substituting from Newton’s second law gives
To get a relationship between net work and the speed given to a system by the net force acting on it, we take and use the equation studied in Motion Equations for Constant Acceleration in One Dimension for the change in speed over a distance if the acceleration has the constant value ; namely, (note that appears in the expression for the net work). Solving for acceleration gives . When is substituted into the preceding expression for , we obtain
The cancels, and we rearrange this to obtain
This expression is called the work-energy theorem , and it actually applies in general (even for forces that vary in direction and magnitude), although we have derived it for the special case of a constant force parallel to the displacement. The theorem implies that the net work on a system equals the change in the quantity . This quantity is our first example of a form of energy.
The net work on a system equals the change in the quantity .
The quantity in the work-energy theorem is defined to be the translational kinetic energy (KE) of a mass moving at a speed . ( Translational kinetic energy is distinct from rotational kinetic energy, which is considered later.) In equation form, the translational kinetic energy,
is the energy associated with translational motion. Kinetic energy is a form of energy associated with the motion of a particle, single body, or system of objects moving together.
We are aware that it takes energy to get an object, like a car or the package in [link] , up to speed, but it may be a bit surprising that kinetic energy is proportional to speed squared. This proportionality means, for example, that a car traveling at 100 km/h has four times the kinetic energy it has at 50 km/h, helping to explain why high-speed collisions are so devastating. We will now consider a series of examples to illustrate various aspects of work and energy.
Suppose a 30.0-kg package on the roller belt conveyor system in [link] is moving at 0.500 m/s. What is its kinetic energy?
Strategy
Because the mass and speed are given, the kinetic energy can be calculated from its definition as given in the equation .
Solution
The kinetic energy is given by
Entering known values gives
which yields
Discussion
Note that the unit of kinetic energy is the joule, the same as the unit of work, as mentioned when work was first defined. It is also interesting that, although this is a fairly massive package, its kinetic energy is not large at this relatively low speed. This fact is consistent with the observation that people can move packages like this without exhausting themselves.

Notification Switch
Would you like to follow the 'Unit 5 - work and energy' conversation and receive update notifications?