| << Chapter < Page | Chapter >> Page > |
A model to account for this is the concept of “activation energy.” For a reaction to occur, at least some bonds in the reactant molecule must be broken, so that atoms can rearrange and new bonds can be created. At the time of collision, bonds are stretched and broken as new bonds are made. For example, in the reaction in Equation (1), O 3 (g) + Cl(g) → O 2 (g) + ClO(g) , one of the O-O bonds in O 3 does not exist after the reaction. Breaking reactant bonds and rearranging the atoms during the collision requires the input of energy. The minimum amount of energy required for the reaction to occur is called the activation energy , E a .
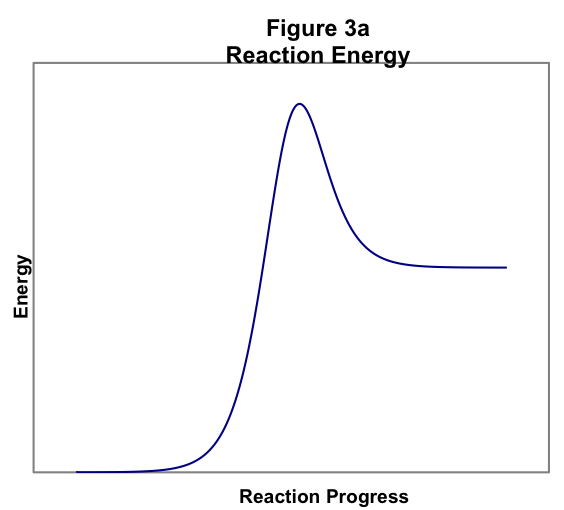
This idea is illustrated in Figure 3, showing conceptually how the energy of the reactants varies as the reaction proceeds. In Figure 3a, the energy is low early in the reaction, when the molecules are still arranged as reactants. As the molecules approach and begin to rearrange, the energy rises sharply, rising to a maximum in the middle of the reaction. This sharp rise in energy is the activation energy, as illustrated. After the middle of the reaction has passed and the molecules are arranged more as products than reactants, the energy begins to fall again. However, the energy does not fall to its original value, so this is an endothermic reaction.
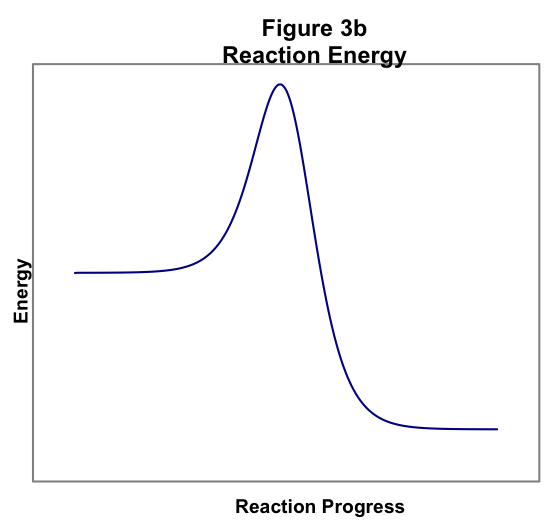
Figure 3b shows the analogous situation for an exothermic reaction. Again, as the reactants approach one another, the energy rises as the atoms begin to rearrange. At the middle of the collision, the energy maximizes and then falls as the product molecules form. In an exothermic reaction, the product energy is lower than the reactant energy.
Figure 3 thus shows that an energy barrier must be surmounted for the reaction to occur, regardless of whether the energy of the products is greater than (Figure 3a) or less than (Figure 3b) the energy of the reactants. This barrier accounts for the temperature dependence of the reaction rate. We know from the Kinetic Molecular Theory that as temperature increases the average energy of the molecules in a sample increases. Therefore, as temperature increases, the fraction of molecules with sufficient energy to surmount the reaction activation barrier increases.
Although we will not show it here, the Kinetic Molecular Theory shows that the fraction of molecules with energy greater than E a at temperature T is proportional to e -E a /RT . This means that the reaction rate and therefore also the rate constant must be proportional to e -E a /RT . Therefore we can write
k(T) = Ae -E a /RT
where A is a new proportionality constant. If we take the logarithm of both sides of Equation (7), we find that
ln k(T) = -E a /RT + ln A
This equation matches the experimentally observed Equation (5). We recall that a graph of ln( k ) versus 1/T is observed to be linear. Now we see that the slope of that graph is equal to – E a /R .
We might think that the activation energy for a reaction is the energy required to break one or more bonds in the reactants. Looking back at Reaction (1) between a Cl atom and an O 3 molecule, we would predict that the activation energy would be equal to the bond energy for breaking one of the O-O bonds in O 3 , which is equal to 400 kJ/mol. However, the activation energy for Reaction (1) has been experimentally found to be 2.1 kJ/mol, enormously less than the energy required to break the O-O bond. How can this be?

Notification Switch
Would you like to follow the 'Concept development studies in chemistry 2013' conversation and receive update notifications?