| << Chapter < Page | Chapter >> Page > |
Everything should be lined up
The pulley, both masses, and all three horizontal segments of cord above the tabletop should be in astraight line. The attachment heights of the cords and the top of the pulley should besuch that all of the cords above the tabletop are horizontal. In other words, there should be no vertical components in any of the forces that act on the cordsabove the tabletop.
Label the tension in each cord
Label the tension in the cord between Mass B and Mass A as P. Label the tension in the cord between Mass C and Mass B as Q Label the tension in the cordbetween the wall and Mass C as R.
Tactile graphics
The svg file that is required to create tactile graphics for this exercise is named Phy1150a1.svg. You should have downloaded that file earlier. This file contains an image that represents the instructions given above .
Figure 3 shows the mirror image that is contained in that file for the benefit of your assistant who will create the tactile graphicfor this exercise.
| Figure 3 . Mirror image of the image from the file named Phy1150a1.svg. |
|---|
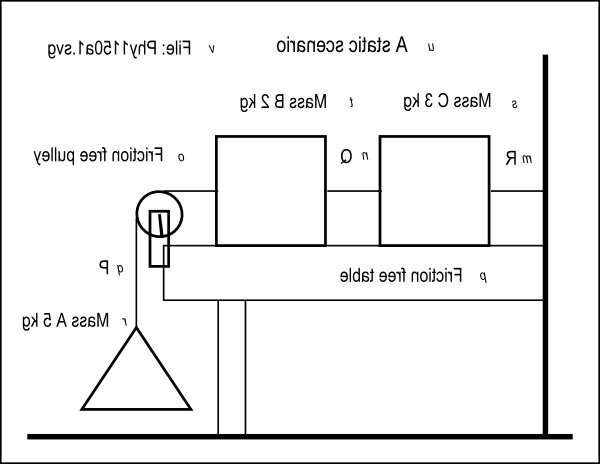 |
Figure 4 shows a non-mirror-image version of the same image.
| Figure 4 . Non-mirror image of the image from the file named Phy1150a1.svg. |
|---|
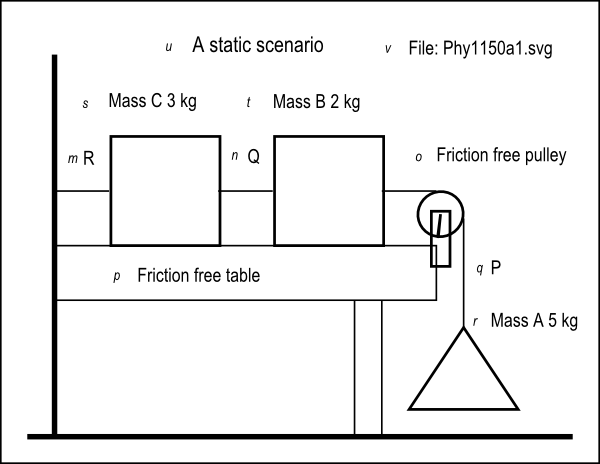 |
Figure 5 shows the key-value pairs that go with the image in the file named Phy1150a1.svg
| Figure 5 . Key-value pairs for the image in the file named Phy1150a1.svg. |
|---|
m: R
n: Qo: Friction free pulley
p: Friction free tableq: P
r: Mass A 5 kgs: Mass C 3 kg
t: Mass B 2 kgu: A static scenario
v: File: Phy1150a1.svg |
The question
What are the tensions P, Q, and R in the individual cord segments when the system is in equilibrium and nothing is moving?
The answers
Mass A is in equilibrium because the upward force exerted by the cord attached to the top of Mass A is equal to the downward force of gravity that isexerted on Mass A.
Therefore, when the system is in equilibrium, the tension P is equal to the weight of Mass A, which is equal to the product of its mass and the accelerationof gravity.
P = 5*kg*9.81*m/s^2 = 49.05 newtons
The effect of the pulley
A single-wheel, frictionless, lightweight pulley as described here changes the direction of the cord, but does not change the tension P in the cord. The tension in the cord is the same on bothsides of the pulley.
Support from the table
Mass B and Mass C are both in vertical equilibrium because their weight is being supported by the table.
Horizontal equilibrium
Mass B is in horizontal equilibrium because the force exerted on one side of the mass by tension Q is equal to the force exerted on the other side of themass by tension P, which is 49.05 newtons.
Mass C is in horizontal equilibrium because the force exerted on one side of the mass by tension R is equal to the force exerted on the other side of themass by tension Q, which as explained above, is 49.05 newtons.
The wall exerts a force that is equal in magnitude and opposite in direction to tension R in the cord that attaches Mass C to the wall.
Tensions are all the same
Therefore, the tensions in all three cords are the same and the force exerted by the wall supports the weight of Mass A hanging by the cord on the other end ofthe chain.

Notification Switch
Would you like to follow the 'Accessible physics concepts for blind students' conversation and receive update notifications?