0.16 Reaction rates  (Page 5/9)

The half-life of a second order reaction differs from the half-life of a first order reaction. From [link] , if we take $\left[A\right]=\frac{1}{2}{\left[A\right]}_0$ , we get

Observation 3: temperature dependence of reaction rates

It is a common observation that reactions tend to proceed more rapidly with increasing temperature. Similarly,cooling reactants can have the effect of slowing a reaction to a near halt. How is this change in rate reflected in the rate lawequation, e.g. [link] ? One possibility is that there is a slight dependence on temperature ofthe concentrations, since volumes do vary with temperature. However, this is insufficient to account for the dramatic changesin rate typically observed. Therefore, the temperature dependence of reaction rate is primarily found in the rate constant, $k$ .

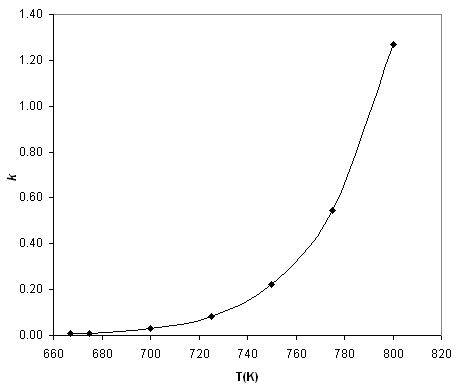
Consider for example the reaction of hydrogen gas with iodine gas at high temperatures, as given in [link] . The rate constant of this reaction at each temperature can be found using the method of initial rates,as discussed above, and we find in [link] that the rate constant increases dramatically as the temperature increases.

As shown in [link] , the rate constant appears to increase exponentially with temperature. After a littleexperimentation with the data, we find in [link] that there is a simple linear relationship between $\ln k$ and $\frac{1}{T}$ .

Rate constant

Rate constant

From [link] , we can see that the data in [link] fit the equation

It is very important to note that the form of [link] and the appearance of [link] are both the same as the equations and graphs for the temperature dependence of theequilibrium constant for an endothermic reaction. This suggests a model to account for the temperature dependence of the rateconstant, based on the energetics of the reaction. In particular, it appears that the reaction rate is related to the amount ofenergy required for the reaction to occur. We will develop this further in the next section.

Collision model for reaction rates

At this point, we have only observed the dependence of reaction rates on concentration of reactants and ontemperature, and we have fit these data to equations called rate laws. Although this is very convenient, it does not provide usinsight into why a particular reaction has a specific rate law or why the temperature dependence should obey [link] . Nor does it provide any physical insights into the order of the reaction or the meaning of theconstants $a$ and $b$ in [link] .

We begin by asking why the reaction rate should depend on the concentration of the reactants. To answerthis, we consider a simple reaction between two molecules in which atoms are transferred between the molecules during the reaction.For example, a reaction important in the decomposition of ozone O ₃ by aerosols is $${\text{O}}_3\left(g\right)+\text{Cl}\left(g\right)\to {\text{O}}_2\left(g\right)+\text{Cl}\text{O}\left(g\right)$$ What must happen for a reaction to occur between anO ₃ molecule and a Cl atom?Obviously, for these two particles to react, they must come into close proximity to one another so that anO atom can be transferred from one to the other. In general, two molecules cannottrade atoms to produce new product molecules unless they are close enough together for the atoms of the two molecules to interact.This requires a collision between molecules.