| << Chapter < Page | Chapter >> Page > |
On occasion objects move within a medium that is itself in motion with respect to an observer. For example, an airplane usually encounters a wind as it flies. The speed of the airplane with respect to a stationary observer situated on the ground will not be the same as the speedometer reading for the plane. In order to calculate the true speed of the plane, it is essential to include the effect due to the wind. In some cases, planes encounter headwinds which will diminish the speed of the plane relative to a stationary observer. I other cases, planes may encounter tail winds which will increase the speed relative to a stationary observer.
Question 1: Let us consider the example where an airplane is traveling with a speed of 880 km/hr with respect to the air. Suppose the airplane encounters a tailwind of velocity 30 km/hr. What is the resultant velocity of the airplane relative to an observer on the ground?
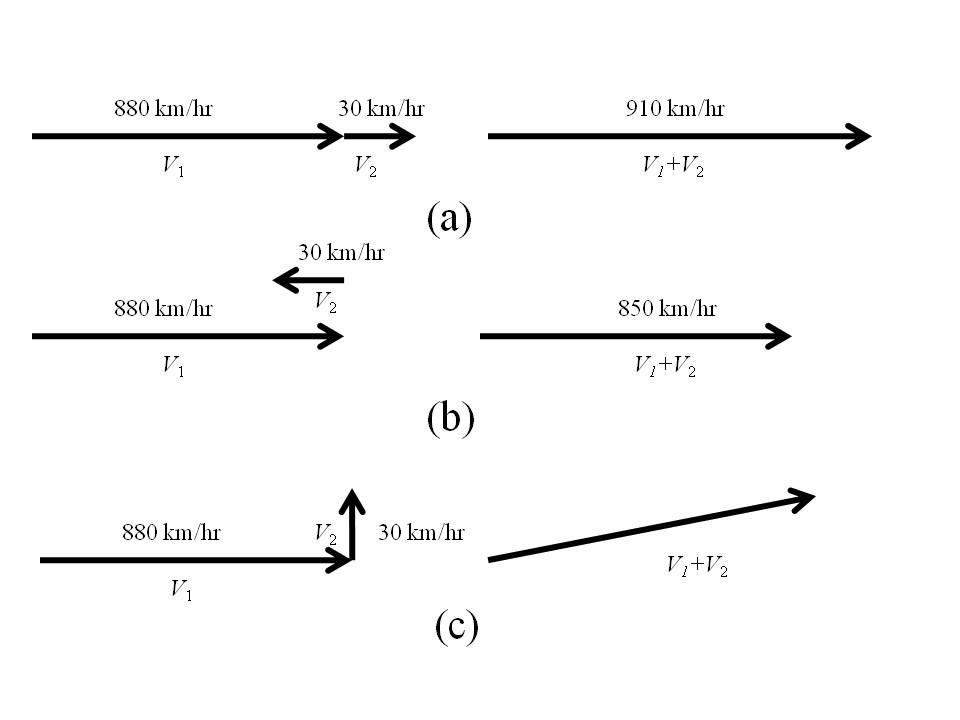
This problem can be addressed using the concept of vector addition. We will represent the velocity of the plane relative to the air as the vector V 1 and that of the tail wind as the vector V 2 . The velocity of the plane relative to a stationary observer on the ground can be found by performing the vector addition of V 1 and V 2 . This addition is accomplished by placing the tail of vector V2 to the head of vector V1. The result, 910 km/m, is shown in Figure 1 (a).
Let us now consider a different situation.
Question 2: Consider the same airplane as in Question 1. However, assume that the airplane is encountering a head wind of 30 km/hr. What is the speed of the plane relative to a stationary observer on the ground?
In this case, the head wind serves to slow the airplane. The situation is reflected in Figure 1 (b). We note that the vector V2 is directed opposite to that of vector V1 due to the fact that the head wind opposes the motion of the airplane. The resulting speed relative to an observer on the ground is computed as 850 km/hr.
Now, we will consider a situation in which we must use our knowledge of vectors and trigonometry to find the correct result.
Question 3: Consider the same airplane as in Question 1. However, assume that the airplane is encountering a cross wind of 30 km/hr. What is the speed of the plane relative to a stationary observer on the ground?
This situation is depicted in Figure 2.
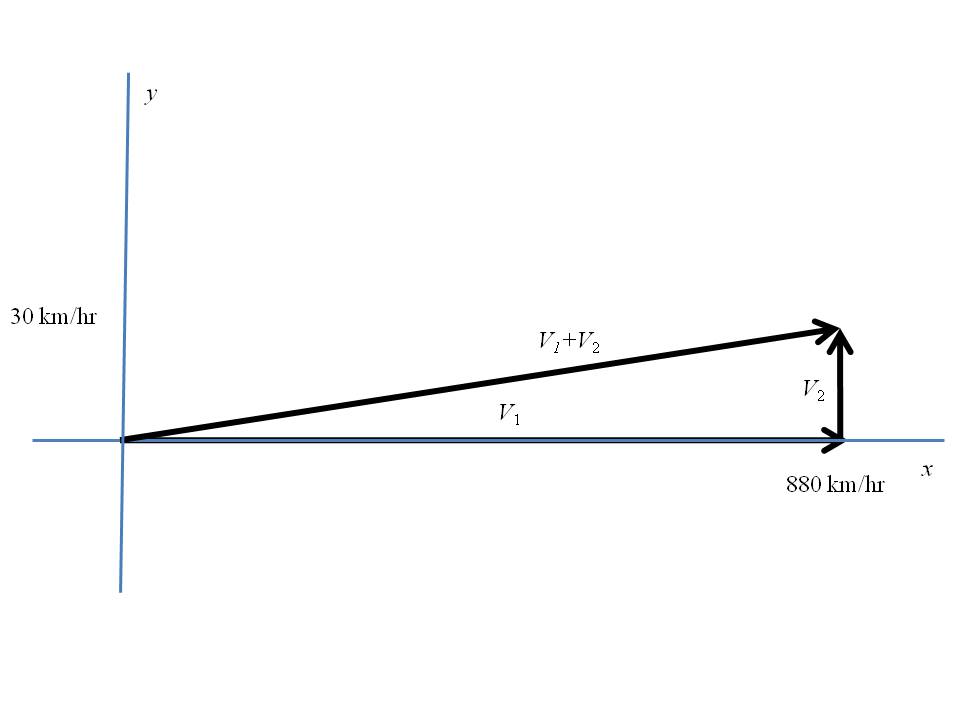
In this case, the speed of the airplane is represented by the length of the sum of vectors, V 1 + V 2 . Using the x-y coordinate system shown in the figure, we note that
and
we may write an expression for this sum in vector form as
To determine the speed of the airplane relative to a stationary observer we must find the magnitude of the vector sum. We can do so by applying the Pythagorean Theorem
Thus, we determine speed of the airplane relative to a stationary observer on the ground to be 881 km/hr.

Notification Switch
Would you like to follow the 'Math 1508 (laboratory) engineering applications of precalculus' conversation and receive update notifications?