| << Chapter < Page | Chapter >> Page > |
| Pressure (torr) | Volume (ml) |
|---|---|
| 760 | 29.0 |
| 960 | 23.0 |
| 1160 | 19.0 |
| 1360 | 16.2 |
| 1500 | 14.7 |
| 1650 | 13.3 |
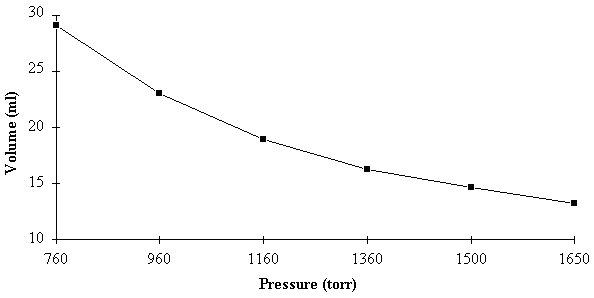
An initial question is whether there is a quantitative relationship between the pressure measurements and thevolume measurements. To explore this possibility, we try to plot the data in such a way that both quantities increase together. Thiscan be accomplished by plotting the pressure versus the inverse of the volume, rather than versus the volume. The data are given in [link] and plotted in [link] .
| Pressure (torr) | Volume (ml) | 1/Volume (1/ml) | Pressure × Volume |
|---|---|---|---|
| 760 | 29.0 | 0.0345 | 22040 |
| 960 | 23.0 | 0.0435 | 22080 |
| 1160 | 19.0 | 0.0526 | 22040 |
| 1360 | 16.2 | 0.0617 | 22032 |
| 1500 | 14.7 | 0.0680 | 22050 |
| 1650 | 13.3 | 0.0752 | 21945 |
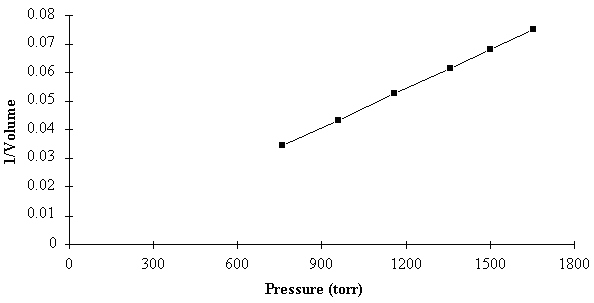
Notice also that, with elegant simplicity, the data points form a straight line. Furthermore, the straight lineseems to connect to the origin . This means that the pressure must simply be a constant multipliedby :
If we multiply both sides of this equation by , then we notice that
In other words, if we go back and multiply the pressure and the volume together for each experiment, we should getthe same number each time. These results are shown in the last column of [link] , and we see that, within the error of our data, all of the data points give thesame value of the product of pressure and volume. (The volume measurements are given to three decimal places and hence areaccurate to a little better than 1%. The values of are all within 1% of each other, so the fluctuations are not meaningful.)
We should wonder what significance, if any, can be assigned to the number22040 torr ml we have observed. It is easy to demonstrate that this"constant" is not so constant. We can easily trap any amount of air in the syringe at atmospheric pressure. This willgive us any volume of air we wish at 760 torr pressure. Hence, the value22040 torr ml is only observed for the particular amount of air we happened tochoose in our sample measurement. Furthermore, if we heat the syringe with a fixed amount of air, we observe that the volumeincreases, thus changing the value of the 22040 torr ml.Thus, we should be careful to note that the product of pressure and volume is a constant for a given amount of air at afixed temperature . This observation is referred to as Boyle's Law , dating to 1662.
The data given in [link] assumed that we used air for the gas sample. (That, of course, was the only gas with which Boyle wasfamiliar.) We now experiment with varying the composition of the gas sample. For example, we can put oxygen, hydrogen, nitrogen,helium, argon, carbon dioxide, water vapor, nitrogen dioxide, or methane into the cylinder. In each case we start with 29.0 ml ofgas at 760 torr and 25°C. We then vary the volumes as in [link] and measure the pressures. Remarkably, we find that the pressure of each gas isexactly the same as every other gas at each volume given. For example, if we press the syringe to a volume of 16.2 ml, we observea pressure of 1360 torr, no matter which gas is in the cylinder. This result also applies equally well to mixtures ofdifferent gases, the most familiar example being air, of course.

Notification Switch
Would you like to follow the 'Concept development studies in chemistry 2012' conversation and receive update notifications?