| << Chapter < Page | Chapter >> Page > |
In electron microscope the electron can be accelerated to higher energy to obtain a finer resolution. It can resolve on the scale of molecules but can barely perceive the atoms.
To resolve at atomic and sub-atomic level we need to go to particle accelerators. Particle Accelerators are gargantuan machines which can be regarded as giant microscopes for probing into the innermost recesses of matter - an awesome complement to the giant telescopes which probe to the edges of the Universe .
To arrive at the resolving power of particle accelerator we must know Special Theory of Relativity and we must make relativistic corrections in order to arrive at the correct resolving power of the particle accelerators. These are described in the Appendix XXXXIV . Here we will just use them to arrive at the resolving power of the particle accelerators.
Relativistic momentum is related to the total energy E by the following relation ship:
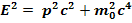
de Broglie wavelength associated with this particle is:
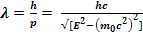
Using Equation (1.99), the resolving power of various particle accelerators operational around the world is tabulated in Table(1.13).[Taken from Table(9.1), “Overview of Particle Physics”, by Abdus Salam, New Physics, edited by Paul Davies, Cambridge University Press, 1992]
Table 1.13. The resolution of the particle accelerators around the World.
| Name&Location | Energy reached | Year | Resolution | Particle detected |
| Rutherford*Manchester,UK. | Alpha decay10MeV,alpha particle’s velocity= 2×10 7 m/s, Alpha particle=4He nucleus; | 1911 | 4.5×10^ -15 m | Nucleus size= 10^ -14 m; Rutherford determined the size to be 30fmBut the correct estimate is 7fm; |
| 1919 | 1.24×10^ -15 m | Protonssize= 10^ -15 m=1fm; | ||
| 1932 | 1.24×10^ -15 m | Neutronssize= 10^ -15 m =1fm | ||
| 1GeV | 1.24×10^ -15 m | |||
| Bepc(e + e - ) Beijing | 4GeV | 1987 | ||
| TRISTAN(e + e - ) Japan | 60GeV | 1987 | ||
| 10GeV | 1979 | 1.24×10^ -16 m | Quarks size= 10^ -16 m | |
| SLC(e + e - ) Stanford,California,USA; | 100GeV | 1987 | 1.24×10^ -17 m | W - , W + &Z 0 detected |
| LEP(I) (e + e - ) Large electron-positron collidorCERN, Geneva; | 100GeV | 1987 | 1.24×10^ -17 m | |
| LEP(II) (e + e - ) CERN,Geneva | 200GeV | 1995 | 6.2×10^ -18 m | Top Quarksdetected |
| HERA(ep)Hamburg | 320GeV | 1991 | 3.87×10^ -18 m | |
| SpSCERN, Geneva | 900GeV | 1986 | 1.38×10^ -18 m | |
| TevatronFermiLab,USA | 1TeV | 1987 | 1.24×10^ -18 m | No excited state of quarks or leptons detected size= 10^ -18 m |
| TevatronFermiLab,USA | 2TeV | 1987 | 6.2×10^ -19 m | |
| UNKSerpukhov,Russia | 3TeV | 1995 | 4.13×10^ -19 m | |
| EeSerpukhov,Russia | 4TeV | ? | 3×10^ -19 m | |
| Large HadronCollider(LHC),CERN,Geneva | 16TeV | ? | 7.75×10^ -20 m | |
| SSC(super particle superconductingCollider),USA; | 40TeV | ? | 3.1×10^ -20 m | |
| 1PeV | ? | 1.24×10^ -21 m | ||
| 1EeV | ? | 1.24×10^ -24 m |
* the first particle accelerator was established at Cavendish Laboratory, Cambridge University. In 1919 Rutherford became the first Director and he was instrumental in establishing the particle accelerator.
In Metal the wavelength is comparable to the lattice constant. This is like light falling through a narrow aperture whose dimension is comparable to the wavelength. Incident light will form a circular diffraction pattern behind the aperture on the target screen. This implies that conducting electron in a metallic lattice is strongly scattered by the lattice centers. Hence it has a very low mobility.
In Semiconductor, the de Broglie wave length is much larger than the lattice constant. Hence lattice scattering is weak and only the gross imperfections cause the scattering. These gross imperfections could be phonons and dislocations extending over several lattice constants. This is what makes conducting electrons much more mobile in semiconductor as compared to that in metal.
In metal, conducting electrons behave like degenerate gas and not quite like ideal gas whereas in semiconductors they behave like non-degenerate gas which is more like ideal gas obeying ideal gas law.
In ideal gas the molecules are far apart, independent of one another and possessing average energy of (3/2)kT whereas in degenerate gas the molecules are closely packed and average kinetic energy is much larger than (3/2)kT. In Table(1.14),
Metals and Semiconductors parameters have been tabulated in the same table.
Table(1.14). Conductivity(σ), Fermi Level(E F ), Mean Free Path(L*) and Mean Free Time(τ) at 0°C for monovalent metals and semiconductors.
| Metal | σ (10 6 S/cm) | ρ(Ω-cm) | n (10^ 22 / cm 3 ) | μ e cm^ 2 / (V-s)= σ/(nq) | E F (eV) | L*(A°) | τ(fs)= m e μ/q ×10^ -4 |
| Li | 0.12 | 8.3 ×10^ -6 | 4.62 | 16.2 | 4.7 | 110 | 9 |
| Na | 0.23 | 4.35 ×10^ -6 | 2.65 | 54.17 | 3.1 | 350 | 31 |
| K | 0.19 | 5.26 ×10^ -6 | 2.1 | 370 | 44 | ||
| Cu | 0.64 | 1.67 ×10^ -6 | 8.5 | 47 | 7.0 | 420 | 27 |
| Ag | 0.68 | 1.47 ×10^ -6 | 5.9 | 72 | 5.5 | 570 | 41 |
| Ge | 47 | n i = 2.25 ×10^ 13 | 3900 | 2106 | 2217 | ||
| Si | 300k | n i = 1.15 ×10^ 10 | 1350 | 729 | 767.6 | ||
| GaAs | 70.5M | n i =2 ×10^6 | 8600 | 4645.5 | 4890 |

Notification Switch
Would you like to follow the 'Electrical and electronic materials science' conversation and receive update notifications?