| << Chapter < Page | Chapter >> Page > |
If you have written parallel programs in G and have a multicore computer, CONGRATULATIONS!!! You have been successfully developing interactive parallel programs that execute in multicore PC processors.
The following sections discuss some multicore programming techniques to improve the performance of G programs.
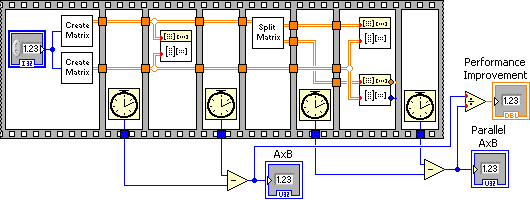
Matrix multiplication is a compute intensive operation that can leverage data parallelism. [link] shows a G program with 8 sequential frames to demonstrate the performance improvement via data parallelism.
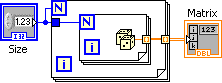
The Create Matrix function generates a square matrix based of size indicated by Size containing random numbers between 0 and 1. The Create Matrix function is shown in [link] .
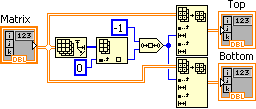
The Split Matrix function determines the number of rows in the matrix and shifts right the resulting number of rows by one (integer divide by 2). This value is used to split the input matrix into the top half and bottom half matrices. The Split Matrix function is shown in [link] .
| Sequence Frame | Operation Description |
|---|---|
| First Frame | Generates two square matrices initialized with random numbers |
| Second Frame | Records start time for single core matrix multiply |
| Third Frame | Performs single core matrix multiply |
| Fourth Frame | Records stop time of single core matrix multiply |
| Fifth Frame | Splits the matrix into top and bottom matrices |
| Sixth Frame | Records start time for multicore matrix multiply |
| Seventh Frame | Performs multicore matrix multiply |
| Eighth Frame | Records stop time of multicore matrix multiply |
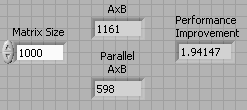
The rest of the calculations determine the execution time in milliseconds of the single core and multicore matrix multiply operations and the performance improvement of using data parallelism in a multicore computer.
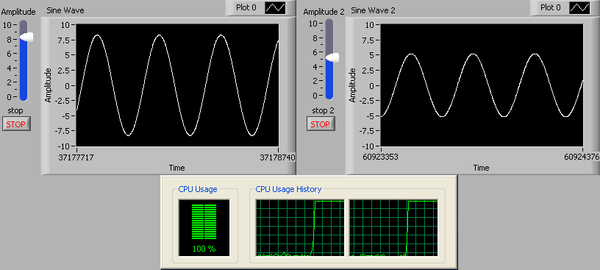
The program was executed in a dual core 1.83 GHz laptop. The results are shown in [link] . By leveraging data parallelism, the same operation has nearly a 2x performance improvement. Similar performance benefits can be obtained with higher multicore processors
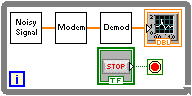
A variety of applications require tasks to be programmed sequentially and continually iterate on these tasks. Most notably are telecommunications applications require simultaneous transmit and receive. In the following example, a simple telecommunications example illustrates how these sequential tasks can be pipelined to leverage multicore environments.
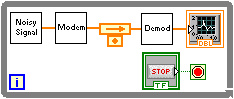
Consider the following simple modulation - demodulation example where a noisy signal is modulated transmitted and demodulated. A typical diagram is shown in [link] .
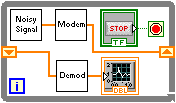
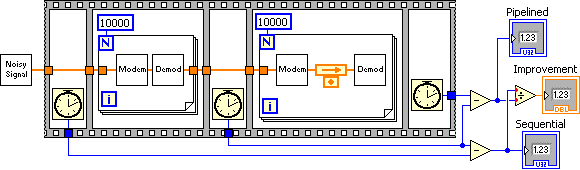
Adding a shift register to the loop allows tasks to be pipelined and be executed in parallel in separate cores should they be available. Task pipelining is shown in [link] .
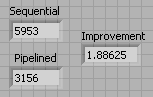
The program below times the sequential task and the pipelined tasks to establish its performance improvement when executed in multicore computers.
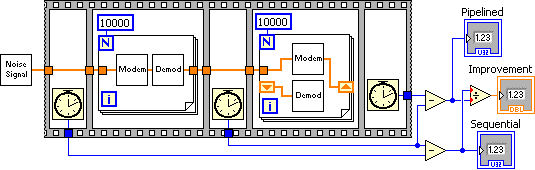
[link] shows the results of running the above G program in a dual core 1.8 GHz laptop. Pipelining shows nearly 2x performance improvement.
Feedback Nodes provide a storage mechanism between loop iterations. They are programmatically identical to the Shift Registers . Feedback Nodes consist of an Initializer Terminal and the Feedback Node itself (see [link] ).
To add a Feedback Node , right click on the Block Diagram window and select Feedback Node from the Functions>>Programming>>Structures pop-up menu. The direction of the Feedback Node can be changed by right clicking on the node and selecting Change Direction .

The diagram shown in [link] is programmatically identical to the diagram in [link] .
Similarly, the diagram in [link] is programmatically identical to that in [link] .

Notification Switch
Would you like to follow the 'Introduction to g programming' conversation and receive update notifications?