0.11 Molecular geometry and electron domain theory  (Page 2/6)

Not all triatomic molecules are bent, however. As a common example,CO ₂ is a linear molecule. Larger polyatomics can have a variety of shapes, as illustrated in [link] . Ammonia,NH ₃ , is a pyramid-shaped molecule, with the hydrogens in an equilateraltriangle, the nitrogen above the plane of this triangle, and a H-N-H angle equal to 107°. The geometry ofCH ₄ is that of a tetrahedron, with all H-C-H angles equal to 109.5°. (See also [link] .) Ethane,C ₂ H ₆ , has a geometry related to that of methane. The two carbons arebonded together, and each is bonded to three hydrogens. Each H-C-H angle is 109.5° and each H-C-C angle is109.5°. By contrast, in ethene, C ₂ H ₄ , each H-C-H bond angle is 116.6° and each H-C-C bondangle is 121.7°. All six atoms of ethene lie in the same plane. Thus,ethene and ethane have very different geometries, despite the similarities in their molecular formulae.

Molecular structures

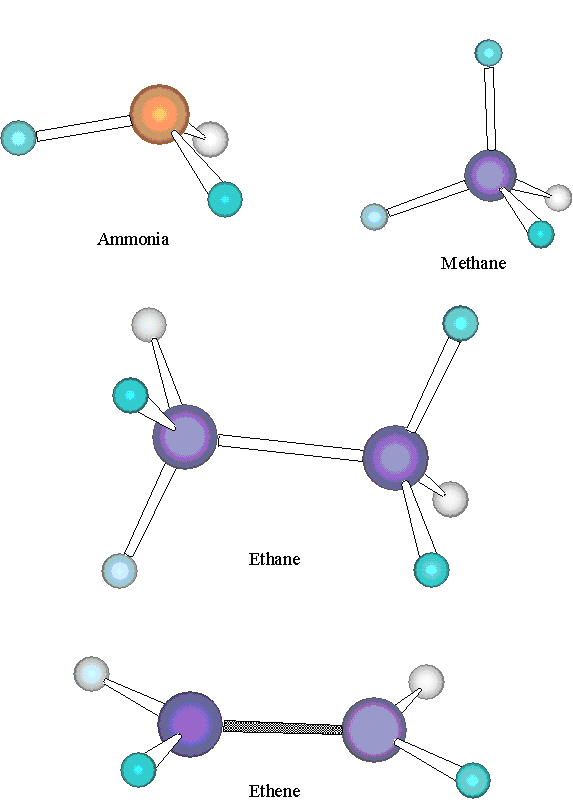
We begin our analysis of these geometries by noting that, in the molecules listed above which do not contain double or triple bonds (H ₂ O, NH ₃ , CH ₄ and C ₂ H ₆ ), the bond angles are very similar, each equal to or very close tothe tetrahedral angle 109.5 °. To account for the observed angle, we begin with our valence shell electron pair sharing model,and we note that, in the Lewis structures of these molecules, the central atom in each bond angle of these molecules contains four pairsof valence shell electrons. For methane and ethane, these four electron pairs are all shared with adjacent bonded atoms, whereasin ammonia or water, one or two (respectively) of the electron pairs are not shared with any other atom. Theseunshared electron pairs are called lone pairs . Notice that, in the two molecules with no lone pairs, all bond angles are exactly equal to the tetrahedral angle, whereas the bond angles are only close in the molecules with lonepairs.

One way to understand this result is based on the mutual repulsion of the negative charges on the valence shellelectrons. Although the two electrons in each bonding pair must remain relatively close together in order to form the bond,different pairs of electrons should arrange themselves in such a way that the distances between the pairs are as large as possible.Focusing for the moment on methane, the four pairs of electrons must be equivalent to one another, since the four C-H bonds areequivalent, so we can assume that the electron pairs are all the same distance from the central carbon atom. How can we positionfour electron pairs at a fixed distance from the central atom but as far apart from one another as possible? A little reflectionreveals that this question is equivalent to asking how to place four points on the surface of a sphere spread out from each otheras far apart as possible. A bit of experimentation reveals that these four points must sit at the corners of a tetrahedron, anequilateral triangular pyramid, as may be seen in [link] . If the carbon atom is at the center of this tetrahedron and the four electron pairs at placed atthe corners, then the hydrogen atoms also form a tetrahedron about the carbon. This is, as illustrated in [link] , the correct geometry of a methane molecule. The angle formed by any two corners of a tetrahedron andthe central atom is 109.5 °, exactly in agreement with the observed angle in methane. This model also works well in predictingthe bond angles in ethane.