1. Home
  2. Kinematics
  3. Kinematics
  4. 1.11 falling objects

0.10 1.11 falling objects  (Page 5/8)

<< Chapter < Page
  Kinematics     Page 5 / 8
Chapter >> Page >

Suppose the ball falls 1.0000 m in 0.45173 s. Assuming the ball is not affected by air resistance, what is the precise acceleration due to gravity at this location?

Strategy

Draw a sketch.

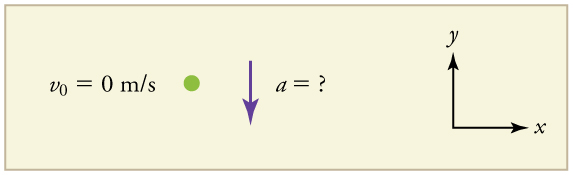
The figure shows a green dot labeled v sub zero equals zero meters per second, a purple downward pointing arrow labeled a equals question mark, and an x y coordinate system with the y axis pointing vertically up and the x axis pointing horizontally to the right.

We need to solve for acceleration a size 12{a} {} . Note that in this case, displacement is downward and therefore negative, as is acceleration.

Solution

1. Identify the knowns. y 0 = 0 ; y = –1 .0000 m ; t = 0 .45173 ; v 0 = 0 size 12{v rSub { size 8{0} } =0} {} .

2. Choose the equation that allows you to solve for a size 12{a} {} using the known values.

y = y 0 + v 0 t + 1 2 at 2 size 12{y=y rSub { size 8{0} } +v rSub { size 8{0} } t+ { {1} over {2} } ital "at" rSup { size 8{2} } } {}

3. Substitute 0 for v 0 size 12{v rSub { size 8{0} } } {} and rearrange the equation to solve for a size 12{a} {} . Substituting 0 for v 0 size 12{v rSub { size 8{0} } } {} yields

y = y 0 + 1 2 at 2 . size 12{y=y rSub { size 8{0} } + { {1} over {2} } ital "at" rSup { size 8{2} } "." } {}

Solving for a size 12{a} {} gives

a = 2 y − y 0 t 2 . size 12{a= { {2 left (y - y rSub { size 8{0} } right )} over {t rSup { size 8{2} } } } "." } {}

4. Substitute known values yields

a = 2 ( − 1 . 0000 m – 0 ) ( 0 . 45173 s ) 2 = − 9 . 8010 m/s 2 , size 12{a= { {2 \( - 1 "." "0000 m–0" \) } over { \( 0 "." "45173 s" \) rSup { size 8{2} } } } = - 9 "." "8010 m/s" rSup { size 8{2} } ,} {}

so, because a = − g size 12{a= - g} {} with the directions we have chosen,

g = 9 . 8010 m/s 2 . size 12{g=9 "." "8010 m/s" rSup { size 8{2} } } {}

Discussion

The negative value for a size 12{a} {} indicates that the gravitational acceleration is downward, as expected. We expect the value to be somewhere around the average value of 9 . 80 m/s 2 size 12{9 "." "80 m/s" rSup { size 8{2} } } {} , so 9 . 8010 m/s 2 size 12{9 "." "8010 m/s" rSup { size 8{2} } } {} makes sense. Since the data going into the calculation are relatively precise, this value for g size 12{g} {} is more precise than the average value of 9 . 80 m/s 2 size 12{9 "." "80 m/s" rSup { size 8{2} } } {} ; it represents the local value for the acceleration due to gravity.

A chunk of ice breaks off a glacier and falls 30.0 meters before it hits the water. Assuming it falls freely (there is no air resistance), how long does it take to hit the water?

We know that initial position y 0 = 0 , final position y = −30 . 0 m , and a = − g = − 9 . 80 m/s 2 . We can then use the equation y = y 0 + v 0 t + 1 2 at 2 to solve for t . Inserting a = − g , we obtain

y = 0 + 0 − 1 2 gt 2 t 2 = 2 y − g t = ± 2 y − g = ± 2 ( − 30.0 m ) − 9.80 m /s 2 = ± 6.12 s 2 = 2.47 s ≈ 2.5 s

where we take the positive value as the physically relevant answer. Thus, it takes about 2.5 seconds for the piece of ice to hit the water.

Section summary

  • An object in free-fall experiences constant acceleration if air resistance is negligible.
  • On Earth, all free-falling objects have an acceleration due to gravity g size 12{g} {} , which averages
    g = 9 . 80 m/s 2 . size 12{g=9 "." "80 m/s" rSup { size 8{2} } } {}
  • Whether the acceleration a should be taken as + g size 12{+g} {} or − g is determined by your choice of coordinate system. If you choose the upward direction as positive, a = − g = − 9 . 80 m /s 2 is negative. In the opposite case, a = +g = 9 . 80 m/s 2 is positive. Since acceleration is constant, the kinematic equations above can be applied with the appropriate + g or − g substituted for a .
  • For objects in free-fall, up is normally taken as positive for displacement, velocity, and acceleration.

Conceptual questions

What is the acceleration of a rock thrown straight upward on the way up? At the top of its flight? On the way down?

An object that is thrown straight up falls back to Earth. This is one-dimensional motion. (a) When is its velocity zero? (b) Does its velocity change direction? (c) Does the acceleration due to gravity have the same sign on the way up as on the way down?

How many times higher could an astronaut jump on the Moon than on Earth if his takeoff speed is the same in both locations (gravitational acceleration on the Moon is about 1/6 of g size 12{g} {} on Earth)?

Problems&Exercises

Assume air resistance is negligible unless otherwise stated.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Kinematics. OpenStax CNX. Sep 11, 2015 Download for free at https://legacy.cnx.org/content/col11878/1.5
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Kinematics' conversation and receive update notifications?

Ask