0.1 Правоаголен декартов координатен систем

Правоаголен декартов координатен систем

Правоаголен Декартов координатен систем или накратко само правоголен координатен систем во рамнина се дефинира преку две бројни оски кои се меѓусебно нормални. Едната оска е хоризонтална и се нарекува апсциса или $x-$ оска, а втората оска која е нормална на $x-$ оската е ордината или $y-$ оска. Пресекот на двете оски е во точката $O$ која се нарекува координатен почеток . На оските се определува единечна точка $E$ , што значи дека $\overline{\text{OE}}=1$ . Постојат координатни системи во кои оските не се меѓусебно нормални и зафаќаат произволен агол, а исто така и отсечките кои се земаат за единечни на двете оски може да се со различни должини. Понатаму, кога ќе зборуваме за координатен систем ќе се мисли на правоаголен координатен систем со еднакви единици на двете оски. Правоаголниот координатен систем се нарекува и Декартов во чест на францускиот математичар и филозоф Рене Декарт (Rene Descartes (1596-165)) или Картезиев координатен систем изведен од латинското име на Декарт-Cartesius.

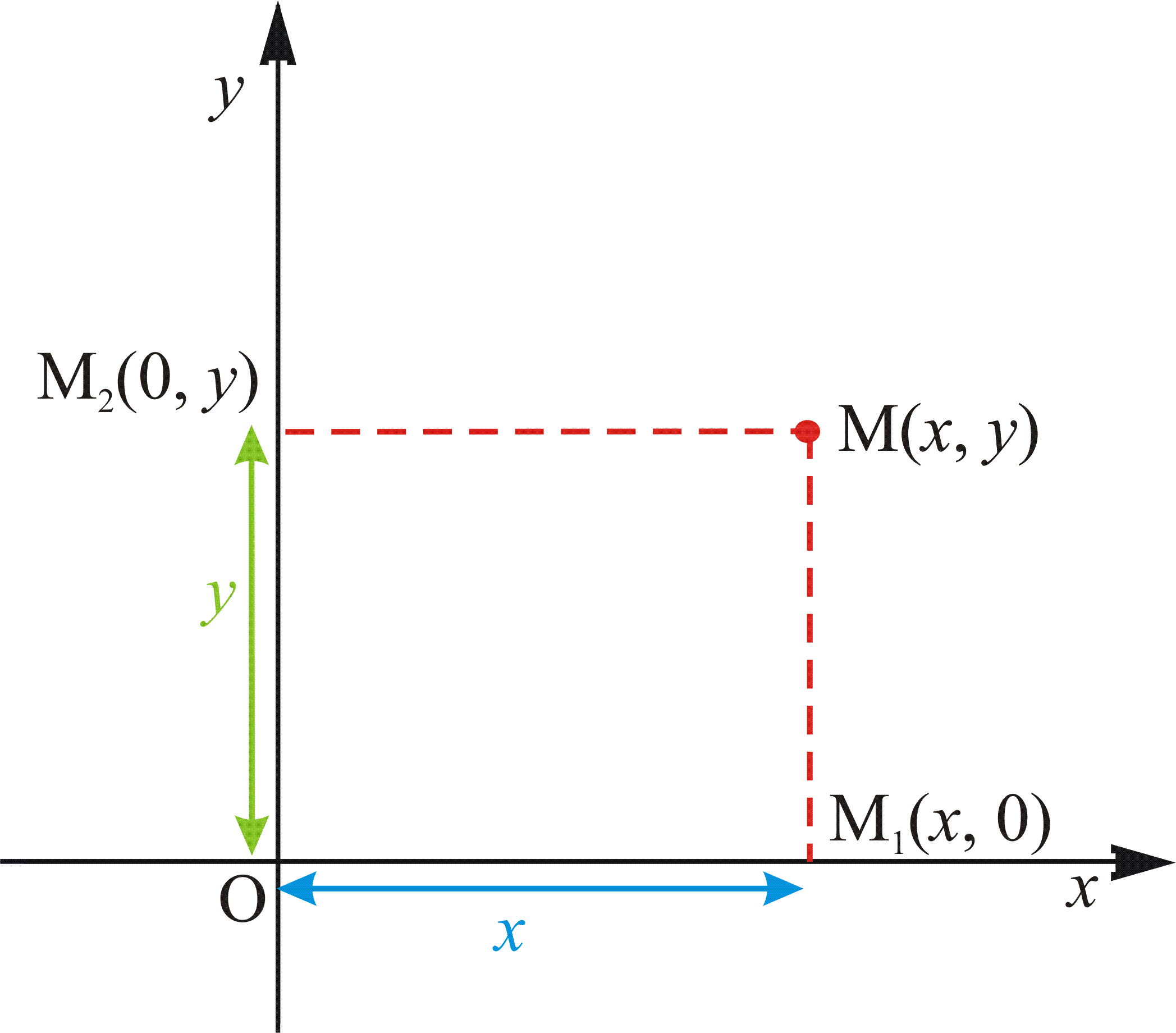
Нека $M$ е произволна точка од рамнината. Од точката $M$ се спуштаат нормали до координатните оски и точките $M_1$ и $M_2$ се пресеци на тие нормали со координатните оски (Сл. 1). Бројот $x=\overline{{\text{OM}}_1}$ се нарекува апсциса на точката $M$ а бројот $y=\overline{{\text{OM}}_2}$ е ордината на точката $M$ и се пишува $M(x,y)$ . Парот реални броеви $(x,y)$ е подреден и неговите компоненти се нарекуваат координати . Тоа значи дека $x$ е првата координата (апсцисата) на точката $M$ , а $y$ е втората координата (ординатата). Према тоа на секоја точка $M$ од рамнината еднозначно и се определува подреден пар реални броеви $(x,y)$ и обратно, на секој подреден пар реални броеви $(x,y)$ му се придружува една и само една точка од рамнината $M$ . Затоа секоја точка $M$ од рамнината се идентификува со нејзините координати $(x,y)$ и со координатниот систем во рамнина се определува еден дводимензионален простор $R^2=R\times R$ .

Координатните оски ја делат рамнината на четири дела кои се нарекуваат квадранти. Во квадрантите координатите на точките се со следните знаци:

I - квадрант: $x>\mathrm{0,}y>0;$

II - квадрант:

III - квадрант:

IV - квадрант: .

За сите точки од $x-$ оската ординатата е $y=0$ , а за сите точки од $y-$ оската вредноста на апсцисата $x=0$ . Координатниот почеток е со координати О (0, 0).

Пример.

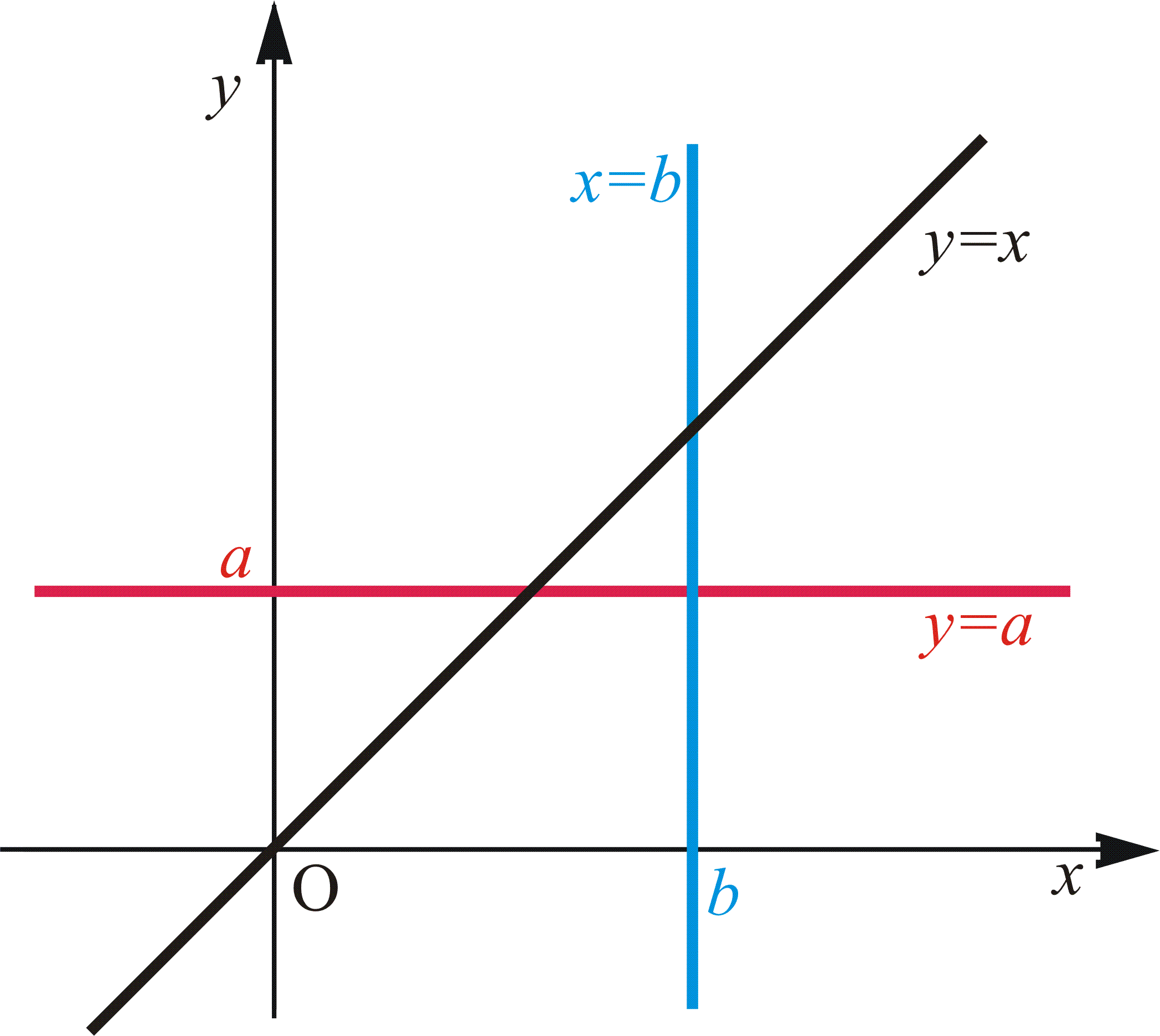
Сите точки со исти ординати $(y=a)$ лежат на права паралелна на $x-$ оската, додека точките со исти апсциси $(x=b)$ се паралелни со $y-$ оската. Точките со исти вредности на апсцисата и ординатата лежат на симетралата на првиот и третиот квадрант, т.е. за нив важи $y=x$ (Сл. 2).