0.1 Butterworth filter properties  (Page 2/2)

• Very close to the ideal near $\omega =0$ and $\omega =\infty$ ,
• Very smooth at all frequencies with a monotonic decrease from $\omega =0$ to $\infty$ , and
• Largest difference between the ideal and actual responses near thetransition at $\omega =1$ where ${\left|F\left(j1\right)\right|}^2=1/2$ .

Although not part of the approximation addressed, the phase curve is also very smooth.

An important feature of the Butterworth filter is the closed- form formula for the solution, $F\left(s\right)$ . The expression for $FF\left(s\right)$ may be determined as

This function has $2N$ poles evenly spaced around a unit radius circle and $2N$ zeros at infinity. The determination of $F\left(s\right)$ is very simple. In order to have a stable filter, $F\left(s\right)$ is selected to have the $N$ left-hand plane poles and $N$ zeros at infinity; $F(-s)$ will necessarily have the right-hand plane poles and the other N zeros at infinity. Thelocation of these poles on the complex $s$ plane for $N=1,2,3$ , and 4 is shown in [link] .

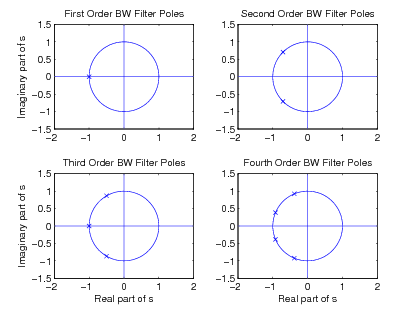
Because of the geometry of the pole positions, simple formulas are easy to derive for the pole locations. If the realand imaginary parts of the pole location are denoted as

the locations of the $N$ poles are given by

for $N$ values of $k$ where

Because the coefficients of the numerator and denominator polynomials of $F\left(s\right)$ are real, the roots occur in complex conjugate pairs. The conjugate pairs in [link] , [link] can be combined to be the roots of second-order polynomials so that for $N$ even, $F\left(s\right)$ has the partially factored form of

for $k=1,3,5,...,N-1$ . For $N$ odd, $F\left(s\right)$ has a single real pole and, therefore, the form

for $k=2,4,6,\cdots ,N-1$

This is a convenient form for the cascade and parallel realizations discussed in elsewhere.

A single formula for the pole locations for both even and odd $N$ is

for $N$ values of $k$ where $k=0,1,2,...,N-1$

One of the important features of the Butterworth filter design formulas is that the pole locations are found by independentcalculations which do not depend on each other or on factoring a polynomial. A FORTRAN program which calculates these values isgiven in the appendix as Program 8. Mathworks has a powerful command for designing analog and digital Butterworth filters.

The classical form of the Butterworth filter given in [link] is discussed in many books [link] , [link] , [link] , [link] , [link] . The less well-known form given in [link] also has many useful applications [link] . If the frequency location of unwanted signals is known, the zeros of the transfer function given by thenumerator can be set to best reject them. It is then possible to choose the pole locations so as to have a passband as flat as theclassical Butterworth filter by using [link] . Unfortunately, there are no formulas for the pole locations; therefore, thedenominator polynomial must be factored.

Summary

Butterworth filter design procedures

This section considers the process of going from given specifications to use of the approximation results derived in theprevious section. The Butterworth filter is the simplest of the four classical filters in that all the approximation effort is placed attwo frequencies: $\omega =0$ and $\omega =\infty$ . The transition from passband to stopband occurs at a normalized frequency of $\omega =1$ . Assuming that this transition frequency or bandedge can later be scaled to any desired frequency, the only parameter tobe chosen in the design process is the order $N$ .

The filter specifications that are consistent with what is optimized in the Butterworth filter are the degree of “flatness" at $\omega =0$ (DC) and at $\omega =\infty$ . The higher the order, the flatter the frequency response at these two points. Because ofthe analytic nature of rational functions, the flatter the response is at $\omega =0$ and $\omega =\infty$ , the closer it stays to the desired response throughout the whole passband and stopband. Anindirect consequence of the filter order is the slope of the response at the transition between pass and stopband. The slope ofthe squared-magnitude frequency response at $\omega =1$ is

The effects of the increased flatness and increased transition slope of the frequency response as N increases are illustrated in Figure 1 from Design of Infinite Impulse Response (IIR) Filters by Frequency Transformations .

In some cases specifications state the response must stay above or below a certainvalue over a given frequency band. Although this type of specification is more compatible with a Chebyshev erroroptimization, it is possible to design a Butterworth filter to meet the requirements. If the magnitude of the frequency response of thefilter over the passband of $0<\omega <{\omega }_P$ must remain between unity and $G$ , where ${\omega }_p<1$ and $G<1$ , the required order is found by the smallest integer $N$ satisfying

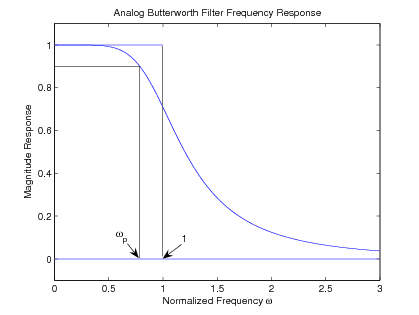
This is illustrated in [link] where $\left|F\right|$ must remain above 0.9 for $\omega$ up to 0.9, i.e., $G$ = 0.9 and ${\omega }_p$ = 0.9. These requirements require an order of at least $N=7$ .

If stopband performance is stated in the form of requiring that the response stay below a certain value for frequency above acertain value, i.e., $\left|F\right|<G$ for $\omega >{\omega }_s$ , the order is determined by the same formula [link] with ${\omega }_p$ replaced by ${\omega }_s$ .

Note $\left|F\left(j1\right)\right|=1/\sqrt{(}2)$ which is called the “half power" frequency because ${\left|F\left(j1\right)\right|}^2=1/2$ . This frequency is normalized to one for the theory but can be scaled to any value for applications.