| << Chapter < Page | Chapter >> Page > |
From we see that . Substituting this into the expression for gives
We write this relationship in two different ways and gain two different insights:
The first relationship in states that the linear velocity is proportional to the distance from the center of rotation, thus, it is largest for a point on the rim (largest ), as you might expect. We can also call this linear speed of a point on the rim the tangential speed . The second relationship in can be illustrated by considering the tire of a moving car. Note that the speed of a point on the rim of the tire is the same as the speed of the car. See [link] . So the faster the car moves, the faster the tire spins—large means a large , because . Similarly, a larger-radius tire rotating at the same angular velocity ( ) will produce a greater linear speed ( ) for the car.
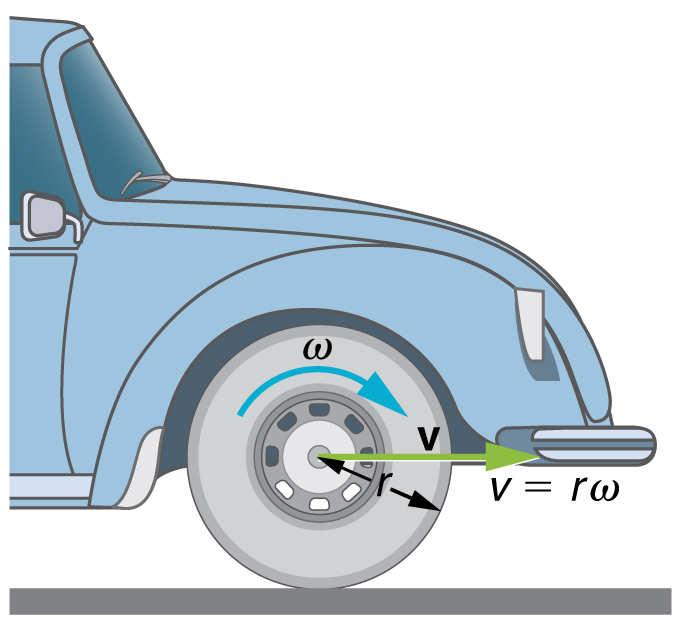
Calculate the angular velocity of a 0.300 m radius car tire when the car travels at (about ). See [link] .
Strategy
Because the linear speed of the tire rim is the same as the speed of the car, we have The radius of the tire is given to be Knowing and , we can use the second relationship in to calculate the angular velocity.
Solution
To calculate the angular velocity, we will use the following relationship:
Substituting the knowns,
Discussion
When we cancel units in the above calculation, we get 50.0/s. But the angular velocity must have units of rad/s. Because radians are actually unitless (radians are defined as a ratio of distance), we can simply insert them into the answer for the angular velocity. Also note that if an earth mover with much larger tires, say 1.20 m in radius, were moving at the same speed of 15.0 m/s, its tires would rotate more slowly. They would have an angular velocity
Both and have directions (hence they are angular and linear velocities , respectively). Angular velocity has only two directions with respect to the axis of rotation—it is either clockwise or counterclockwise. Linear velocity is tangent to the path, as illustrated in [link] .
where arc length is distance traveled along a circular path and is the radius of curvature of the circular path. The quantity is measured in units of radians (rad), for which
where a rotation takes place in a time . The units of angular velocity are radians per second (rad/s). Linear velocity and angular velocity are related by
There is an analogy between rotational and linear physical quantities. What rotational quantities are analogous to distance and velocity?
Semi-trailer trucks have an odometer on one hub of a trailer wheel. The hub is weighted so that it does not rotate, but it contains gears to count the number of wheel revolutions—it then calculates the distance traveled. If the wheel has a 1.15 m diameter and goes through 200,000 rotations, how many kilometers should the odometer read?
723 km
(a) What is the period of rotation of Earth in seconds? (b) What is the angular velocity of Earth? (c) Given that Earth has a radius of at its equator, what is the linear velocity at Earth’s surface?
A baseball pitcher brings his arm forward during a pitch, rotating the forearm about the elbow. If the velocity of the ball in the pitcher’s hand is 35.0 m/s and the ball is 0.300 m from the elbow joint, what is the angular velocity of the forearm?
117 rad/s
A truck with 0.420-m-radius tires travels at 32.0 m/s. What is the angular velocity of the rotating tires in radians per second? What is this in rev/min?
76.2 rad/s
728 rpm
Integrated Concepts When kicking a football, the kicker rotates his leg about the hip joint.
(a) If the velocity of the tip of the kicker’s shoe is 35.0 m/s and the hip joint is 1.05 m from the tip of the shoe, what is the shoe tip’s angular velocity?
(b) The shoe is in contact with the initially stationary 0.500 kg football for 20.0 ms. What average force is exerted on the football to give it a velocity of 20.0 m/s?
(c) Find the maximum range of the football, neglecting air resistance.
(a) 33.3 rad/s
(b) 500 N
(c) 40.8 m

Notification Switch
Would you like to follow the 'Unit 4 - uniform circular motion and universal law of gravity' conversation and receive update notifications?