| << Chapter < Page | Chapter >> Page > |

Suppose you want to walk from one point to another in a city with uniform square blocks, as pictured in [link] .
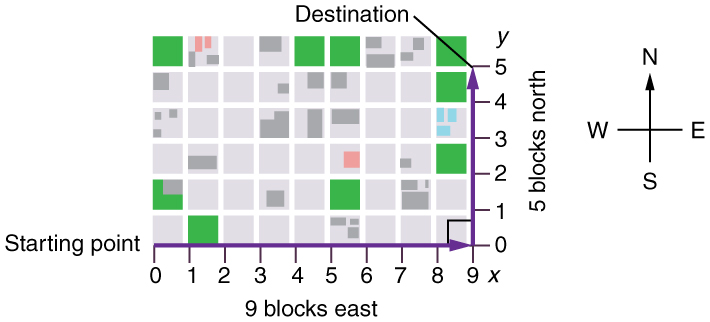
The straight-line path that a helicopter might fly is blocked to you as a pedestrian, and so you are forced to take a two-dimensional path, such as the one shown. You walk 14 blocks in all, 9 east followed by 5 north. What is the straight-line distance?
An old adage states that the shortest distance between two points is a straight line. The two legs of the trip and the straight-line path form a right triangle, and so the Pythagorean theorem, , can be used to find the straight-line distance.
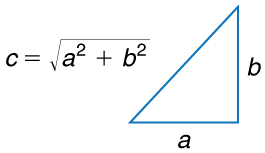
The hypotenuse of the triangle is the straight-line path, and so in this case its length in units of city blocks is , considerably shorter than the 14 blocks you walked. (Note that we are using three significant figures in the answer. Although it appears that “9” and “5” have only one significant digit, they are discrete numbers. In this case “9 blocks” is the same as “9.0 or 9.00 blocks.” We have decided to use three significant figures in the answer in order to show the result more precisely.)
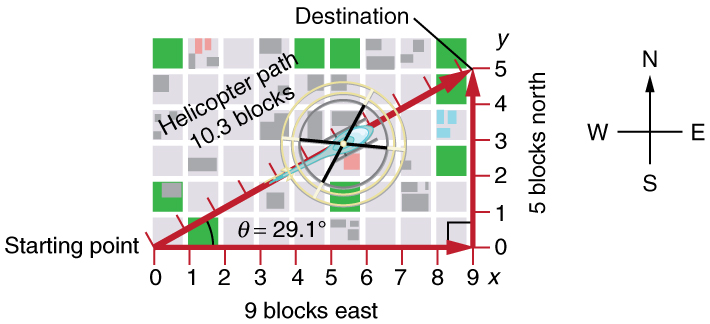
The fact that the straight-line distance (10.3 blocks) in [link] is less than the total distance walked (14 blocks) is one example of a general characteristic of vectors. (Recall that vectors are quantities that have both magnitude and direction.)
As for one-dimensional kinematics, we use arrows to represent vectors. The length of the arrow is proportional to the vector’s magnitude. The arrow’s length is indicated by hash marks in [link] and [link] . The arrow points in the same direction as the vector. For two-dimensional motion, the path of an object can be represented with three vectors: one vector shows the straight-line path between the initial and final points of the motion, one vector shows the horizontal component of the motion, and one vector shows the vertical component of the motion. The horizontal and vertical components of the motion add together to give the straight-line path. For example, observe the three vectors in [link] . The first represents a 9-block displacement east. The second represents a 5-block displacement north. These vectors are added to give the third vector, with a 10.3-block total displacement. The third vector is the straight-line path between the two points. Note that in this example, the vectors that we are adding are perpendicular to each other and thus form a right triangle. This means that we can use the Pythagorean theorem to calculate the magnitude of the total displacement. (Note that we cannot use the Pythagorean theorem to add vectors that are not perpendicular. We will develop techniques for adding vectors having any direction, not just those perpendicular to one another, in Vector Addition and Subtraction: Graphical Methods and Vector Addition and Subtraction: Analytical Methods .)

Notification Switch
Would you like to follow the '2d kinematics' conversation and receive update notifications?