Figure 1
Published: June 27,
2006
by Richard G. Baldwin
Java Programming Notes # 2362
DSP and adaptive filtering
Digital Signal Processing (DSP) is showing up in everything from cell phones to hearing aids and rock concerts. A particularly interesting branch of DSP is adaptive filtering. This is a scenario where the characteristics of the digital processor change with time, circumstances, or both.
Seventh in a series
This is the seventh lesson in a series designed to teach you about adaptive filtering in Java. The first lesson, titled Adaptive Filtering in Java, Getting Started, introduced you to the topic of adaptively designing a convolution filter using an LMS adaptive algorithm.
A general-purpose adaptive engine
The third lesson in the series, titled A General-Purpose LMS Adaptive Engine in Java, presented and explained a general-purpose LMS adaptive engine written in Java. That engine can be used to solve a wide variety of adaptive problems.
Adaptive noise cancellation
The previous lesson titled Adaptive Noise Cancellation using Java showed you how to accomplish the third item, Noise Cancellation, in the following list of common applications of adaptive filtering:
Adaptive prediction
This lesson presents and explains a program named Adapt09, which demonstrates the use of adaptive filtering for the prediction of future values in a time series.
Viewing tip
You may find it useful to open another copy of this lesson in a separate browser window. That will make it easier for you to scroll back and forth among the different listings and figures while you are reading about them.
Supplementary material
I recommend that you also study the other lessons in my extensive collection of online Java tutorials. You will find those lessons published at Gamelan.com. However, as of the date of this writing, Gamelan doesn't maintain a consolidated index of my Java tutorial lessons, and sometimes they are difficult to locate there. You will find a consolidated index at www.DickBaldwin.com.
In preparation for understanding the material in this lesson, I recommend that you also study the lessons identified in the References section of this document.
What is adaptive prediction?
Quite simply, adaptive prediction is the ability to adaptively design a convolution filter that can be applied to a time series in order to predict future values of the time series. I will let you use your own imagination (or perhaps research on the web) to come up with various scenarios where this may be useful.
The program named Adapt09
The purpose of this program is to illustrate an adaptive prediction filter. The user can experiment with adaptive prediction by making changes to the following program parameters and observing the printed and graphic results:
A block diagram
See the following URL for a brief description and a block diagram of an adaptive prediction filter.
http://www.mathworks.com/access/helpdesk/help/toolbox/filterdesign/
adaptiv8.html#5576
I will refer to this block diagram later when discussing this program.
Classes required
This program requires the following classes:
The source code for the class named Adapt09 is presented in Listing 14 near the end of the lesson. The source code for the other classes in the above list can be found in the lessons referred to in the References section of this lesson.
A general-purpose adaptive engine
This program uses the adaptive engine named AdaptEngine02 to adaptively develop a convolution prediction filter. The adaptive engine is represented by the shaded portion of the block diagram.
One of the inputs to the adaptive engine is the current sample of the sum of signal plus noise, shown as d(k) in the block diagram. This is the target of the prediction process.
The other input to the adaptive engine is an historical sample of signal plus noise shown as x(k) in the block diagram.
The adaptive engine develops a convolution filter (shown as Adaptive Filter in the block diagram) that attempts to use historical signal plus noise samples to predict the value of the current sample of signal plus noise (target). Thus, the program attempts to adaptively develop a convolution filter that can operate on a time series to predict a future value of the time series.
The distance in time to the future value being predicted is a user input parameter.
The iterative process
The program performs 9890 iterations during which the convolution filter coefficients are adaptively updated. Then the adaptive update process is disabled. The program then performs 9890 more iterations during which time the quality of the prediction is measured and reported.
The prediction quality
The quality of the prediction is measured by:
Signal and noise characteristics
The signal consists of a pure tone at a frequency that is one eighth of the sampling frequency (eight samples per cycle). The peak-to-peak value of the signal prior to scaling is 2.
The noise consists of white noise produced by a random number generator with a uniform distribution between -1.0 and 1.0 prior to scaling.
The scaled signal is added to the scaled white noise.
Conditioning the signal plus noise
The sum of signal plus white noise can be passed through a variable-width band pass filter with a center frequency equal to one-eighth of the sampling frequency.
(The band pass filter is not shown in the block diagram. Consider it to be to the left of the block diagram with s(k) as its output.)
The center frequency of the band pass filter is the same as the frequency of the signal. Thus, the signal plus noise consists of a pure tone surrounded by noise for which the noise bandwidth can be controlled by the user. The frequency band for the noise is centered on the signal frequency. The user controls the signal level and the noise level and hence the signal-to-noise ratio.
The band pass filter
The band pass filter consists of a convolution filter in the form of a truncated sinusoid with a frequency of one-eighth of the sampling frequency. The user specifies the length of the convolution filter, (up to a limit of 128 coefficients), thereby specifying the bandwidth of the filter. The bandwidth of the filter is roughly proportional to the reciprocal of the length of the convolution filter.
The shape of the amplitude response of the pass band for the filter is roughly that of a sin(x)/x function.
The graphic program output
The program produces three graphs in a vertical stack on the screen as shown in Figure 1.
Figure 1 |
The three graphs display the following information in order from top to bottom:
Multiple stacked pages
The bottom graph consists of multiple pages stacked on top of one another. (There are 230 samples plotted in each trace on each page.) You must physically move the pages on the top of the stack to view the pages further down. The pages on the top of the stack represent the results produced early in the adaptive process while those further down represent the results produced later in the adaptive process.
The time series
The four time series that are plotted in the bottom graph are, from top to bottom (in the colors indicated):
The printed program output
In addition to the graphic output, the program displays the quality of the prediction process and the program parameters on the command-line screen as shown in Figure 2.
RMS target: 6.410217370961125 RMS error: 1.4675827349708308 Percent error: 22.894430095601994 feedbackGain: 1.0E-5 numberAdaptiveIterations: 9890 adaptiveFilterLength: 26 predictionDistance: 1 signalScale: 0.0 noiseScale: 87.5 bpFilterLength: 128 rmsAveragingLength: 9890 Figure 2 |
User input
User input is provided by way of command-line parameters. If no command-line parameters are provided, default values are used for the program parameters.
The command-line parameters in order are:
Program testing
The program was tested using J2SE 5.0 and WinXP. J2SE 5.0 or later is required.
Before getting into the program details, I'm going to show you some experimental results.
The bottom line at the beginning
As you will see from these experimental results, the ability to predict future values in a time series tends to vary inversely with the bandwidth of the time series. Future values of narrow-band time series can be predicted reasonably well. Future values of wide-band time series cannot be predicted well at all.
I will begin by showing you results for the two extremes:
A pure tone
A pure tone has the narrowest band width of all time series (theoretically it has zero width). As you will see, a pure tone in the absence of noise is totally predictable.
The results of applying the adaptive prediction process to a pure tone are shown in Figure 3 and Figure 4.
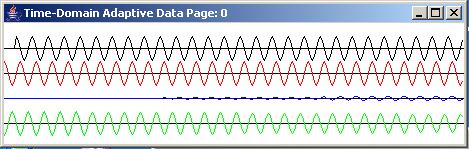 |
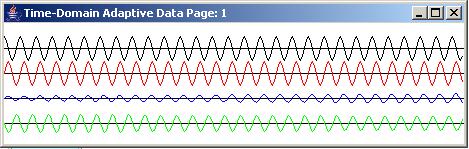 |
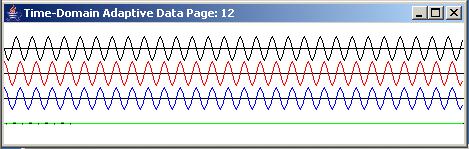 |
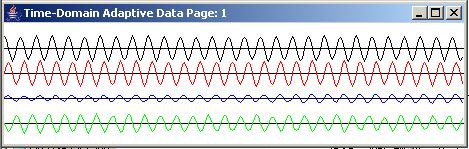
Figure 3 |
The time series data
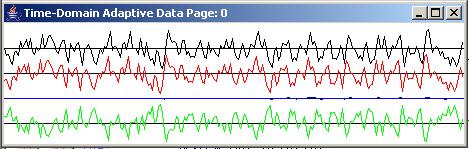
Going from top to bottom, Figure 3 shows the time series output for the first, second, and thirteenth pages. (Recall that each trace on each page shows 230 samples of the time series data.) The black trace shows the input to the adaptive filter and the red trace shows the target. The blue trace shows the output from the adaptive filter. The green trace shows the error.
In the top page of Figure 3, the blue output is small and the green error is large. By the thirteenth page, the blue output is almost an exact match for the red target and the green error has been reduced to almost zero.
The numeric prediction error
The numeric prediction error (along with some other information) is shown in Figure 4.
RMS target: 8.838387896368511 RMS error: 0.0027504970625717136 Percent error: 0.031119895334100794 feedbackGain: 1.0E-5 numberAdaptiveIterations: 9890 adaptiveFilterLength: 3 predictionDistance: 6 signalScale: 12.5 noiseScale: 0.0 bpFilterLength: 1 rmsAveragingLength: 9890 Figure 4 |
As you can see in Figure 4, the prediction error was only 0.03-percent of the target.
The prediction distance
Also note in Figure 4 that the prediction distance is six samples. In other words, the adaptive process was asked to design a convolution filter that can predict the value of a pure tone six samples into the future.
The adaptive filter length
Also note that the adaptive filter contained only three coefficients in this scenario.
A somewhat pathological case
This is a case for which it is easy to develop a purely deterministic mathematical solution. All that is required is the solution of a set of simultaneous equations that will produce a convolution filter whose amplitude response is unity and whose phase response is a specified value at the frequency of the tone.
The case of a pure tone in the total absence of noise rarely occurs in the real world. Thus, the mathematical solution described above can produce undesirable results. While the amplitude response can be forced to unity at a particular frequency by solving the simultaneous equations, it is likely to be much larger than unity at other frequencies. If there is noise at those other frequencies, that noise will be amplified in the output of the adaptive filter. A much more realistic scenario is shown in Figure 5 and Figure 6.
A more realistic scenario
Figure 5 shows the results of applying the adaptive prediction process (with a three-coefficient prediction filter) to a tone buried in white noise. The peak amplitude of the tone is ten times greater than the peak amplitude of the noise. Figure 5 shows the same three pages that were shown for the pure tone in Figure 3.
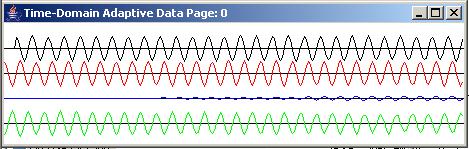 |
 |
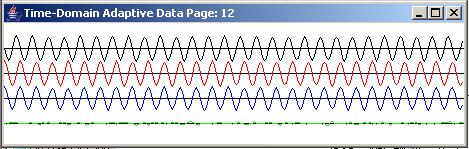 |
Figure 5 |
The error is not zero
As you can see, the green error is not zero in Figure 5. In fact, the error never goes to zero. As shown in Figure 6, the prediction error is approximately ten percent of the target.
RMS target: 8.866400709397215 RMS error: 0.9514570545236098 Percent error: 10.731040539541494 feedbackGain: 1.0E-5 numberAdaptiveIterations: 9890 adaptiveFilterLength: 3 predictionDistance: 6 signalScale: 12.5 noiseScale: 1.25 bpFilterLength: 1 rmsAveragingLength: 9890 Figure 6 |
A mathematical solution
While there is a non-adaptive mathematical solution for this scenario, it is by no means a simple one and it is not deterministic. The solution involves computing a cross-correlation function between the signal plus noise and the target and then solving a matrix equation to compute the coefficient values for the prediction filter.
Probably better behaved
The frequency response of the adaptive filter developed for this scenario is probably better behaved than is the case for the pure tone shown in Figure 3. It is unlikely that the amplitude response for this scenario will amplify the noise at frequencies other than the frequency of the tone, at least not in significant ways. (This characteristic could be improved by using a longer adaptive filter.)
Increased prediction error
On the other hand, the prediction error for this scenario is significantly greater than the prediction error for the scenario involving the pure tone in the absence of noise.
(By the way, increasing the filter length for the scenario involving the pure tone probably won't improve the final prediction error, but it may cause the adaptive process to converge to a solution more quickly.)
Predictability of white noise
Now, let's take a look at the other extreme: white noise.
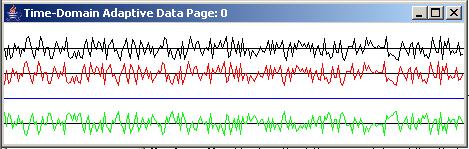
Figure 7 and Figure 8 show the results of applying the adaptive prediction process to white noise produced by a random number generator.
 |
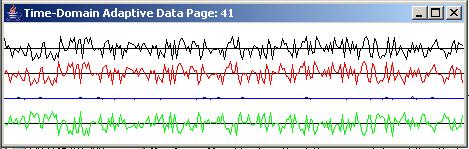 |
Figure 7 |
The time series output
Figure 7 shows the time-series output at the beginning of the adaptive process and at the end of 9890 adaptive iterations.
(The bottom panel of Figure 7 shows the final 230 adaptive iterations ending at iteration number 9890.)
As you can see, the blue output from the adaptive filter in the bottom panel of Figure 7 is very nearly zero, and the green error hasn't been reduced at all. The error trace is simply an upside-down version of the target trace.
The numeric prediction error
Figure 8 shows the prediction error to be about 100 percent.
RMS target: 7.195524462306129 RMS error: 7.225023010529711 Percent error: 100.40995688887043 feedbackGain: 1.0E-5 numberAdaptiveIterations: 9890 adaptiveFilterLength: 26 predictionDistance: 1 signalScale: 0.0 noiseScale: 12.5 bpFilterLength: 1 rmsAveragingLength: 9890 Figure 8 |
Conclusion
The conclusion is that white noise is not predictable, even over a prediction distance of only one sample with an adaptive filter having 26 coefficients.
(If it were found to be predictable, that would indicate that the random number generator used to produce the white noise doesn't really produce random numbers after all.)
Predictability of narrow-band noise
So far, we have seen experimental results for the following three scenarios:
On the basis of those experiments, we have concluded:
These scenarios represented the extremes. Now let's look at some in-between scenarios involving narrow-band time series for which the bandwidth is greater than a single frequency. We will begin with a scenario where the bandwidth has been reduced to that shown in the right panel of Figure 9.
 |
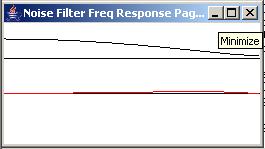 |
Figure 9 |
|
The display format
The curve in the left panel of Figure 9 shows a convolution filter having two coefficients.
The top curve in the right panel shows the amplitude response of that convolution filter computed and displayed from a frequency of zero to the Nyquist folding frequency. The bottom curve in the right panel shows the phase response of the convolution filter.
Apply band pass filter to white noise
This convolution filter was applied to the white noise, producing an output time series having approximately one-half the bandwidth of the white noise.
(Note that there are several different ways to measure bandwidth. This estimate is based on the width of the lobe between the three-db down points in the amplitude response.)
The time series data
The adaptive prediction process was applied to this time series in an attempt to predict the value of the time series with a prediction distance of one sample and an adaptive filter length of 26 coefficients. The results are shown in Figure 10 and Figure 11.
 |
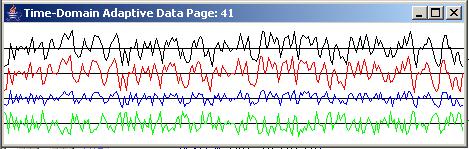 |
Figure 10 |
The top panel in Figure 10 shows the time series at the beginning of the run. The bottom panel shows the time series ending at adaptive iteration number 9890. As you can see in the bottom panel of Figure 9, the blue output trace from the adaptive filter does look something like the red target trace. The green error trace in the bottom panel is smaller than the green output trace at the beginning of the run in the top panel.
The numeric prediction error
As shown in Figure 11, the prediction error was reduced from 100 percent for white noise to about 82 percent for this scenario. Reducing the bandwidth of the white noise caused the time series to become partially predictable.
RMS target: 8.889476886391076 RMS error: 7.3078201913053915 Percent error: 82.20753914657176 feedbackGain: 1.0E-5 numberAdaptiveIterations: 9890 adaptiveFilterLength: 26 predictionDistance: 1 signalScale: 0.0 noiseScale: 12.5 bpFilterLength: 2 rmsAveragingLength: 9890 Figure 11 |
Bandwidth at one-sixteenth of white noise
Figure 12, Figure 13, and Figure 14 show the results of applying the adaptive prediction process to a time series having a bandwidth approximately equal to one-sixteenth of the bandwidth of the white noise shown in Figure 7.
 |
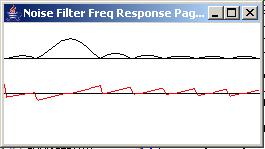 |
Figure 12 |
|
The left panel in Figure 12 shows the impulse response of a convolution filter having sixteen coefficients in the form of a truncated sinusoid. The right panel in Figure 12 shows the frequency response of the convolution filter computed and displayed from a frequency of zero to the Nyquist folding frequency. The bandwidth of the filter is approximately one-sixteenth of the bandwidth of the white noise shown in Figure 7 when measured at the three-db down points.
Apply the band pass filter
The filter shown in Figure 12 was applied to the white noise producing the time series shown in the top trace in each panel of Figure 13.
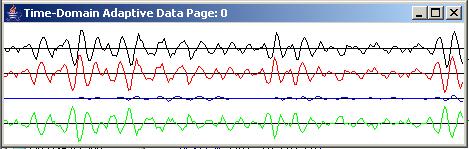 |
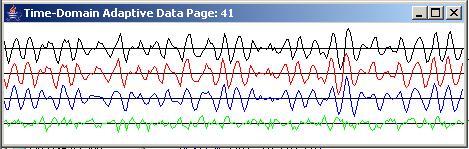 |
Figure 13 |
The time series output
This time series was subjected to the adaptive prediction process with a prediction distance of one sample and an adaptive filter length of 26 coefficients, producing the results shown in Figure 13 and Figure 14.
The top panel in Figure 13 shows the time series at the beginning of the run. The bottom panel shows the time series at the end of 9890 adaptive iterations. As you can see, the blue output trace from the prediction filter is a reasonably good representation of the red target trace in the bottom panel of Figure 13. Also, the green error trace in the bottom panel is much smaller than the green error trace at the beginning of the run in the top panel.
The numeric prediction error
In fact, this reduction in bandwidth caused the prediction error to be reduced to about forty-six percent as shown in Figure 14.
RMS target: 7.490714340573816 RMS error: 3.479276931459588 Percent error: 46.447865627633355 feedbackGain: 1.0E-5 numberAdaptiveIterations: 9890 adaptiveFilterLength: 26 predictionDistance: 1 signalScale: 0.0 noiseScale: 37.5 bpFilterLength: 16 rmsAveragingLength: 9890 Figure 14 |
Predictability of a very narrow-band time series
Let's examine one more set of experimental results. These are the results produced by the default program parameters that are used if the user doesn't provide the appropriate number of command-line parameters.
For this experiment, we will reduce the bandwidth to approximately 1/128 of the bandwidth of the white noise shown in Figure 7.
The band pass filter
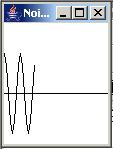
Figure 15 shows the convolution filter having 128 coefficients.
Figure 15 |
Figure 16 shows the frequency response of the convolution filter, computed and displayed from a frequency of zero to the Nyquist folding frequency.
Figure 16 |
Apply the band pass filter
As you can see, the bandwidth of this filter is quite narrow, as compared to Figure 12, for example. This filter was applied to white noise, producing the top (black) trace in both panels of Figure 17.
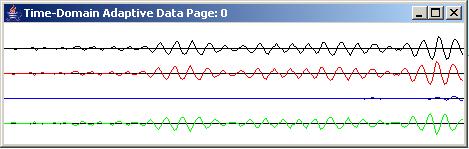 |
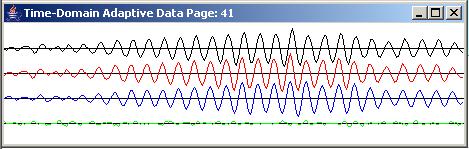 |
Figure 17 |
As before, the top panel in Figure 17 shows the time series at the beginning of the run. The bottom panel shows the time series at the end of 9890 adaptive iterations. The output from the adaptive filter (blue) is a good replica of the target (red). Thus, the green error trace is quite small.
The numeric prediction error
Figure 18 shows that this reduction in bandwidth resulted in a reduction in the prediction error to about 23 percent.
RMS target: 6.482512172567318 RMS error: 1.4847104556284205 Percent error: 22.903319208738477 feedbackGain: 1.0E-5 numberAdaptiveIterations: 9890 adaptiveFilterLength: 26 predictionDistance: 1 signalScale: 0.0 noiseScale: 87.5 bpFilterLength: 128 rmsAveragingLength: 9890 Figure 18 |
This is the longest convolution filter (128 coefficients) that is supported by the program in its current state. However, this limitation has nothing to do with the process of applying the filter to the noise. Rather, it has to do with the method named displayFreqResponse that is used to compute and display the frequency response of the filter. As an exercise, you may find it interesting to eliminate that limitation and observe how the prediction error behaves as you use longer and longer convolution filters (narrower and narrower bandwidth).
Probably the easiest way to eliminate the limitation of 128 filter coefficients would be to disable the call to the method named displayFreqResponse and simply forego the computation and display of the frequency response. By now, you should have a pretty good idea how the frequency response behaves as you increase the length of the convolution filter anyway.
(In addition, you will need to disable the code that limits the filter length to 128 when you enter a command-line parameter greater than 128.)
That's it for experimental results. I recommend that you do some experimentation on your own to gain a better understanding as to how the predictability behaves with respect to the various program parameters.
Now let's see some code.
The class named Adapt09
The class named Adapt09 is presented in its entirety in Listing 14 near the end of the lesson.
I will discuss the program in fragments. The beginning of the class named Adapt09 and the beginning of the main method are shown in Listing 1.
class Adapt09{
public static void main(String[] args){
//Default parameter values
double feedbackGain = 0.00001;
int numberAdaptiveIterations = 9890;//fixed value
int adaptiveFilterLength = 26;
int predictionDistance = 1;
double signalScale = 0;
double noiseScale = 87.5;
int bpFilterLength = 128;//Must be <= 128.
int rmsAveragingLength = 9890;//fixed value
if(args.length == 6){
//Get and save command-line parameters.
feedbackGain = Double.parseDouble(args[0]);
adaptiveFilterLength = Integer.parseInt(args[1]);
predictionDistance = Integer.parseInt(args[2]);
signalScale = Double.parseDouble(args[3]);
noiseScale = Double.parseDouble(args[4]);
bpFilterLength = Integer.parseInt(args[5]);
if(bpFilterLength > 128){
//Make sure this value is not greater than 128.
bpFilterLength = 128;
System.out.println(
"bpFilterLength must be <= 128");
System.out.println("Using bpFilterLength = 128");
}//end if
}else{
System.out.println(
"Using default program parameters.");
}//end else
|
All of the code in Listing 1 is straightforward and shouldn't require explanation beyond the comments embedded in the code.
Create the band pass filter
The code in Listing 2:
//Create an array object to store the bandpass filter
// coefficients.
double[] bpFilterOperator = new double[bpFilterLength];
//Instantiate a new object of the Adapt09 class.
Adapt09 thisObject = new Adapt09();
//Prepare the bandpass filter,which is a truncated
// sinusoid with a frequency of one-eighth of the
// sampling frequency.
for(int cnt = 0;cnt < bpFilterLength;cnt++){
bpFilterOperator[cnt] = thisObject.getCosine(cnt);
}//end for loop
|
The getCosine method
For every scenario, the band pass filter is simply a truncated cosine function with a frequency that is one-eighth of the sampling frequency. Thus, the coefficient values repeat with eight coefficient values occurring during each cycle of the cosine function.
The source code for the getCosine method is shown in Listing 14 near the end of the lesson. That code is straightforward and shouldn't require further explanation.
The remainder of the main method
The remainder of the main method is shown in Listing 3.
//Invoke the method named process.
thisObject.process(feedbackGain,
numberAdaptiveIterations,
rmsAveragingLength,
adaptiveFilterLength,
signalScale,
noiseScale,
bpFilterOperator,
predictionDistance);
//Display program parameters at the end of the run.
System.out.println("\nfeedbackGain: " + feedbackGain);
System.out.println("numberAdaptiveIterations: "
+ numberAdaptiveIterations);
System.out.println("adaptiveFilterLength: "
+ adaptiveFilterLength);
System.out.println("predictionDistance: "
+ predictionDistance);
System.out.println("signalScale: " + signalScale);
System.out.println("noiseScale: " + noiseScale);
System.out.println("bpFilterLength: "
+ bpFilterLength);
System.out.println("rmsAveragingLength: "
+ rmsAveragingLength);
}//end main
|
The code in Listing 3 invokes the process method of the Adapt09 class, where all the hard work is done. When the process method returns, the code in Listing 3 displays some summary information (see Figure 18 for example) and terminates the program.
The process method
Listing 4 shows the beginning of the process method.
void process(double feedbackGain,
int numberAdaptiveIterations,
int rmsAveragingLength,
int adaptiveFilterLength,
double signalScale,
double noiseScale,
double[] bpFilterOperator,
int predictionDistance){
//Display the bandpassFilterOperator
//First instantiate a plotting object.
PlotALot01 bpFilterPlotObj = new PlotALot01(
"Noise Filter Operator",
(bpFilterOperator.length * 2) + 8,148,70,2,0,0);
//Feed the data to the plotting object.
for(int cnt = 0;cnt < bpFilterOperator.length;cnt++){
bpFilterPlotObj.feedData(40*bpFilterOperator[cnt]);
}//end for loop
//Cause the graph to be displayed on the computer
// screen in the upper left corner.
bpFilterPlotObj.plotData(0,0);
//Now compute and plot the frequency response of the
// bandpass filter.
//Instantiate a plotting object for two channels of
// frequency response data. One channel is for
// the amplitude and the other channel is for the
// phase.
PlotALot03 bpFilterFreqPlotObj = new PlotALot03(
"Noise Filter Freq Response",264,148,35,2,0,0);
//Compute the frequency response and feed the results
// to the plotting object.
displayFreqResponse(
bpFilterOperator,bpFilterFreqPlotObj,128,0);
//Cause the frequency response data stored in the
// plotting object to be displayed on the screen in
// the middle position.
bpFilterFreqPlotObj.plotData(0,148);
|
All of the code in Listing 4 is the same as, or very similar to code that has been previously explained in lessons referred to in the References section of this lesson. Therefore, it shouldn't be necessary to provide further explanation of that code beyond the comments contained in Listing 4.
Two delay lines
Listing 5 instantiates an array object that will be used as a delay line for the signal plus white noise data in order to convolve the samples with the band pass filter later.
double[] whiteNoiseDelayLine =
new double[bpFilterOperator.length];
|
Note that the length of the delay line is determined by the length of the array created earlier and referred to by the reference variable named bpFilterOperator. In other words, the length of the delay line matches the length of the convolution operator used to implement the band pass filter. The length of the convolution filter is a user input parameter.
Listing 6 instantiates an array object that will be used as a delay line for the filtered signal plus noise data. This delay line is used to obtain a target sample that is advanced in time relative to the data that is used to predict the target. The target sample is advanced in time by a number of samples equal to predictionDistance.
double[] signalPlusNoiseDelayLine =
new double[predictionDistance + 1];
|
The delay line created in Listing 6 corresponds to the box labeled Delay in the block diagram.
A plotting object and working variables
Listing 7 instantiates a plotting object that will be used to plot the four channels of time-series data shown in Figure 3. This code is similar to code that was explained in previous lessons referred to in the References section of this lesson.
//Instantiate a plotting object for four channels of
// time-series data at 230 samples per page.
int sampPerPage = 230;
PlotALot05 timePlotObj = new PlotALot05(
"Time-Domain Adaptive Data",
(2*sampPerPage + 8),148,25,2,0,0);
//Declare and initialize working variables.
double output = 0;
double err = 0;
double target = 0;
double input = 0;
double signal = 0;
double whiteNoise = 0;
boolean adaptOn;
double targetSumSq = 0;
double errSumSq = 0;
|
Listing 7 also declares and initializes some working variables.
None of the code in Listing 7 should require further explanation.
An adaptive engine object
Listing 8 instantiates an object of the class named AdaptEngine02 to handle the adaptive behavior of this program. This class was explained earlier in the lesson titled Adaptive Identification and Inverse Filtering using Java. That explanation won't be repeated here.
AdaptEngine02 adapter = new AdaptEngine02(
adaptiveFilterLength,feedbackGain);
|
The object of the AdaptEngine02 class represents the shaded portion of the block diagram.
Perform adaptive iterations
Listing 9 contain the beginning of a for loop that is used to perform the required number of iterations. The required number of iterations is the sum of the specified number of adaptive iterations plus the non-adaptive iterations that are used to compute the percent error after the adaptive update process is disabled.
for(int cnt = 0;
cnt < numberAdaptiveIterations + rmsAveragingLength;
cnt++){
|
Routine processing steps
Listing 10 performs a number of routine processing steps. These steps are either completely straightforward, or are very similar to code that has been explained in previous lessons, which are referred to in the References section of this lesson. Therefore, no explanation beyond the embedded comments will be provided in this lesson.
//The following variable is used to control whether
// or not the adapt method of the adaptive engine
// updates the filter coefficients when it is called.
// The filters are updated when this variable is
// true and are not updated when this variable is
// false.
adaptOn = true;
//Get and scale the next sample of white noise data
// from a random number generator. Before scaling by
// noiseScale, the values are uniformly distributed
// from -1.0 to 1.0.
whiteNoise = noiseScale*(2*(random() - 0.5));
//Get and scale the next sample of signal. The
// signal is a pure tone with a frequency equal to
// one-eighth of the sampling frequency. Before
// scaling by signalScale, the peak-to-peak value
// is 2.
signal = signalScale * getCosine(cnt);
//Insert the signal plus white noise data into the
// delay line that will be used to convolve the
// signal plus white noise data with the bandpass
// filter.
double signalPlusNoise = whiteNoise + signal;
flowLine(whiteNoiseDelayLine,signalPlusNoise);
//Declare a variable to receive the filtered signal
// plus noise sample.
double filteredSignalPlusNoise = 0;
//Apply the bandpass filter operator to the signal
// plus white noise data. If the filter length is 1,
// bypass the filtering operation and use the raw
// signal plus white noise.
if(bpFilterOperator.length == 1){
filteredSignalPlusNoise = signalPlusNoise;
}else{
filteredSignalPlusNoise = reverseDotProduct(
whiteNoiseDelayLine,
bpFilterOperator)/(bpFilterOperator.length/2.0);
}//end else
//Insert the filtered signal plus noise into the
// delay line that is used to obtain a time-advanced
// sample of the target.
flowLine(
signalPlusNoiseDelayLine,filteredSignalPlusNoise);
//Declare a variable that will be populated with the
// results returned by the adapt method of the
// adaptive engine.
AdaptiveResult result = null;
//Disable adaptive updates when the specified number
// of adaptive iterations has been performed.
if(cnt > numberAdaptiveIterations){
adaptOn = false;
}//end if
|
Perform the adaptive processing
The most important code in this class is contained in Listing 11. This code establishes the appropriate input values and invokes the adapt method of the AdaptEngine02 object to perform the adaptive updates to the adaptive filter coefficients.
input = signalPlusNoiseDelayLine[0];//historical samp
target =
signalPlusNoiseDelayLine[predictionDistance];
result = adapter.adapt(input,target,adaptOn);
|
Just to get our bearings, input in Listing 11 corresponds to x(k) in the block diagram. Similarly, target in Listing 11 corresponds to d(k) in the block diagram.
The oldest data in the delay line referred to by signalPlusNoiseDelayLine in Listing 11 is the data value at index 0.
The newest data in the delay line is the data value at an index value of predictionDistance. (The length of the delay line is predictionDistance + 1.)
Thus, the oldest value in the delay line is fed into the adaptive filter as x(k) in the block diagram. The newest value in the delay line is used to compute the prediction error as shown by d(k) in the block diagram. As a result, the LMS algorithm attempts to develop an adaptive convolution filter that will act on the incoming time series to predict the value of a sample that is predictionDistance samples in the future.
Complete the for loop
Listing 12 completes the for loop that controls the required number of iterations.
//Get and save adaptive results.
output = result.output;
err = result.err;
//Compute values that will be used later to compute
// the percent error. This computation is performed
// only after adaptive updates have been disabled.
if(!adaptOn){
//Accumulate the sum of the squares of the target
// and error values.
targetSumSq += target * target;
errSumSq += err * err;
}//end if
//Feed the time series data to the plotting object.
// Plot only two pages of data after adaptive updates
// are disabled.
if(cnt <= numberAdaptiveIterations + 2*sampPerPage){
timePlotObj.feedData(input,target,output,err);
}//end if
}//End for loop on required number of iterations.
|
The code in Listing 12 is straightforward and shouldn't require an explanation beyond the embedded comments.
Complete the adapt method
Listing 13 shows the remaining code in the adapt method of the AdaptEngine02 object.
//Compute and display the mean square values
double rmsTarget =
sqrt(targetSumSq/rmsAveragingLength);
double rmsError = sqrt(errSumSq/rmsAveragingLength);
System.out.println("\nRMS target: " + rmsTarget);
System.out.println("RMS error: " + rmsError);
System.out.println(
"Percent error: " + 100.0*(rmsError)/(rmsTarget));
//Cause the data stored in the plotting object to be
// plotted.
timePlotObj.plotData(0,296);
}//end process method
|
This code is straightforward and shouldn't require further explanation.
I encourage you to copy the code for the class named Adapt09 from the section titled Complete Program Listings. Compile and execute the program. Experiment with the code. Make changes to the code, recompile, execute, and observe the results of your changes.
Modify the following program parameters and observe the results of your changes. See if you can explain the results of your changes.
For example, what happens if you use a large value for feedbackGain? What happens if you use a very small value for feedbackGain? What happens if you use a negative value for feedbackGain? Can you explain the results that you experience?
What happens if you use a large value for predictionDistance?
In particular I encourage you to make the changes suggested in the section titled An exercise for the student and evaluate the results of those changes.
Other classes required
In addition to the class named Adapt09, you will need access to the following classes. The source code for these classes can be found in the lessons indicated.
In this lesson, I showed you how to use a Java adaptive filter to predict future values in a time series. I also introduced you to the relationship between the properties of the time series and the quality of the prediction.
In preparation for understanding the material in this lesson, I recommend that you study the material in the following previously-published lessons:
Links to the lessons in the above list are available at Digital Signal Processing-DSP.
A complete listings of the class discussed in this lesson is shown in Listing 14 below.
/*File Adapt09.java
Copyright 2005, R.G.Baldwin
The purpose of this program is to illustrate an adaptive
prediction system. The user can experiment with adaptive
prediction by making changes to the following parameters
and observing printed and graphic results:
feedbackGain
adaptiveFilterLength
predictionDistance
signalScale
noiseScale
bandpassFilterLength (and hence bandwidth)
See the following URL for a brief description and a block
diagram of an adaptive prediction system.
http://www.mathworks.com/access/helpdesk/help/toolbox/
filterdesign/adaptiv8.html#5576
This program requires the following classes:
Adapt09.class
AdaptEngine02.class
AdaptiveResult.class
ForwardRealToComplex01.class
PlotALot01.class
PlotALot03.class
PlotALot05.class
This program uses the adaptive engine named AdaptEngine02
to adaptively develop a convolution prediction filter. One
of the inputs to the adaptive engine is the current sample
of the sum of signal plus noise. This is the target of the
prediction process. The other input to the adaptive engine
is an historical sample of signal plus noise.
The adaptive engine develops a convolution filter that
attempts to use historical signal plus noise samples to
predict the value of the current sample of signal plus
noise (target). Thus, the program attempts to adaptively
develop a convolution filter that can operate on a time
series to predict a future value of the time series. The
distance in time to the future value is a user input
parameter.
The program performs 9890 iterations during which the
convolution filter coefficients are adaptively updated.
Then the adaptive update process is disabled. The program
then performs 9890 more iterations during which the
quality of the prediction is measured and reported.
The quality of the prediction is measured by:
1. Computing the RMS value of the target averaged over
9890 samples.
2. Computing the RMS value of the prediction error
averaged over 9890 samples.
3. Computing the percentage of the RMS target value
represented by the RMS error.
The signal consists of a pure tone at a frequency that is
one eighth of the sampling frequency (eight samples per
cycle). The peak-to-peak value of the signal prior to
scaling is 2.
The noise consists of white noise produced by a random
number generator with a uniform distribution between
-1.0 and 1.0 prior to scaling.
The scaled signal is added to the scaled white noise.
The sum of signal plus white noise can be passed through a
bandpass filter with a center frequency equal to one-
eighth of the sampling frequency. The center frequency of
the bandpass filter is the same as the frequency of the
signal.
Thus, the signal plus noise consists of a pure tone
surrounded by noise for which the noise bandwidth can be
controlled by the user. The frequency band for the noise
is centered on the signal frequency. The user controls the
signal level and the noise level, and hence the
signal-to-noise ratio.
The bandpass filter consists of a convolution filter in the
form of a truncated sinusoid with a frequency of one-eighth
of the sampling frequency. The user specifies the length
of the convolution filter, (up to a limit of 128
coefficients), thereby specifying the bandwidth which is
roughly proportional to the reciprocal of the length of the
convolution filter. The shape of the amplitude response of
the pass band for the filter is roughly that of
a sin(x)/x function.
The program produces three graphs in a vertical stack on
the screen. The graphs display the following information
in order from top to bottom:
1. The bandpass convolution filter used to filter the raw
signal plus noise.
2. The frequency response of the bandpass filter used to
filter the raw signal plus noise.
3. Four traces of adaptive time-series data.
Graph 3 consists of multiple pages stacked on top of one
another. You must move the pages on the top of the stack
to view the pages further down. The pages on the top of
the stack represent the results produced early in the
adaptive process while those further down represent the
results produced later in the adaptive process.
The four time series that are plotted are, from top to
bottom in the colors indicated:
1. (Black) The historical signal plus noise input to the
adaptive prediction filter.
2. (Red) The signal plus noise target for the adaptive
prediction filter.
3. (Blue) The output from the adaptive prediction filter.
4. (Green) The error, which is the difference between the
red target and the blue output from the adaptive
prediction filter. Ideally, this trace approaches zero as
the process converges to a solution.
User input is provided by way of command-line parameters.
If no command-line parameters are provided, default values
are used for the program parameters. The command-line
parameters in order are:
1. double feedbackGain: The gain used in the adaptive
feedback loop. The default value is 0.00001.
2. int adaptiveFilterLength: The default value is 26.
3. int predictionDistance: The distance in the future,
(measured in samples), that the adaptive process attempts
to predict the value of signal plus noise (target). The
default value is 1 sample.
4. double signalScale: The default value is 0. Adjust
this and the following parameter to adjust the signal to
noise ratio, and also to cause the time-series plots to be
in good plotting range.
5. double noiseScale: The default value is 87.5.
6. int bandpassFilterLength: The length of the
convolution filter that is applied to the raw signal plus
noise. This value must be less than or equal to 128. If
it is greater than 128, it is automatically set to 128.
Tested using J2SE 5.0 and WinXP. J2SE 5.0 or later is
required.
**********************************************************/
import static java.lang.Math.*;//J2SE 5.0 req
class Adapt09{
public static void main(String[] args){
//Default parameter values
double feedbackGain = 0.00001;
int numberAdaptiveIterations = 9890;//fixed value
int adaptiveFilterLength = 26;
int predictionDistance = 1;
double signalScale = 0;
double noiseScale = 87.5;
int bpFilterLength = 128;//Must be <= 128.
int rmsAveragingLength = 9890;//fixed value
if(args.length == 6){
//Get and save command-line parameters.
feedbackGain = Double.parseDouble(args[0]);
adaptiveFilterLength = Integer.parseInt(args[1]);
predictionDistance = Integer.parseInt(args[2]);
signalScale = Double.parseDouble(args[3]);
noiseScale = Double.parseDouble(args[4]);
bpFilterLength = Integer.parseInt(args[5]);
if(bpFilterLength > 128){
//Make sure this value is not greater than 128.
bpFilterLength = 128;
System.out.println(
"bpFilterLength must be <= 128");
System.out.println("Using bpFilterLength = 128");
}//end if
}else{
System.out.println(
"Using default program parameters.");
}//end else
//Create an array object to store the bandpass filter
// coefficients.
double[] bpFilterOperator = new double[bpFilterLength];
//Instantiate a new object of the Adapt09 class.
Adapt09 thisObject = new Adapt09();
//Prepare the bandpass filter,which is a truncated
// sinusoid with a frequency of one-eighth of the
// sampling frequency.
for(int cnt = 0;cnt < bpFilterLength;cnt++){
bpFilterOperator[cnt] = thisObject.getCosine(cnt);
}//end for loop
//Invoke the method named process.
thisObject.process(feedbackGain,
numberAdaptiveIterations,
rmsAveragingLength,
adaptiveFilterLength,
signalScale,
noiseScale,
bpFilterOperator,
predictionDistance);
//Display program parameters at the end of the run.
System.out.println("\nfeedbackGain: " + feedbackGain);
System.out.println("numberAdaptiveIterations: "
+ numberAdaptiveIterations);
System.out.println("adaptiveFilterLength: "
+ adaptiveFilterLength);
System.out.println("predictionDistance: "
+ predictionDistance);
System.out.println("signalScale: " + signalScale);
System.out.println("noiseScale: " + noiseScale);
System.out.println("bpFilterLength: "
+ bpFilterLength);
System.out.println("rmsAveragingLength: "
+ rmsAveragingLength);
}//end main
//-----------------------------------------------------//
//This is the primary adaptive processing and plotting
// method for the program.
void process(double feedbackGain,
int numberAdaptiveIterations,
int rmsAveragingLength,
int adaptiveFilterLength,
double signalScale,
double noiseScale,
double[] bpFilterOperator,
int predictionDistance){
//Display the bandpassFilterOperator
//First instantiate a plotting object.
PlotALot01 bpFilterPlotObj = new PlotALot01(
"Noise Filter Operator",
(bpFilterOperator.length * 2) + 8,148,70,2,0,0);
//Feed the data to the plotting object.
for(int cnt = 0;cnt < bpFilterOperator.length;cnt++){
bpFilterPlotObj.feedData(40*bpFilterOperator[cnt]);
}//end for loop
//Cause the graph to be displayed on the computer
// screen in the upper left corner.
bpFilterPlotObj.plotData(0,0);
//Now compute and plot the frequency response of the
// bandpass filter.
//Instantiate a plotting object for two channels of
// frequency response data. One channel is for
// the amplitude and the other channel is for the
// phase.
PlotALot03 bpFilterFreqPlotObj = new PlotALot03(
"Noise Filter Freq Response",264,148,35,2,0,0);
//Compute the frequency response and feed the results
// to the plotting object.
displayFreqResponse(
bpFilterOperator,bpFilterFreqPlotObj,128,0);
//Cause the frequency response data stored in the
// plotting object to be displayed on the screen in
// the middle position.
bpFilterFreqPlotObj.plotData(0,148);
//Instantiate an array object that will be used as a
// delay line for the signal plus white noise data in
// order to convolve the samples with the bandpass
// filter.
double[] whiteNoiseDelayLine =
new double[bpFilterOperator.length];
//Instantiate an array object that will be used as a
// delay line for the filtered signal plus noise data.
// This delay line is used to obtain a target sample
// advanced in time relative to the data that is used
// to predict the target. The target sample is
// advanced in time by a number of samples equal to
// predictionDistance.
double[] signalPlusNoiseDelayLine =
new double[predictionDistance + 1];
//Instantiate a plotting object for four channels of
// time-series data at 230 samples per page.
int sampPerPage = 230;
PlotALot05 timePlotObj = new PlotALot05(
"Time-Domain Adaptive Data",
(2*sampPerPage + 8),148,25,2,0,0);
//Declare and initialize working variables.
double output = 0;
double err = 0;
double target = 0;
double input = 0;
double signal = 0;
double whiteNoise = 0;
boolean adaptOn;
double targetSumSq = 0;
double errSumSq = 0;
//Instantiate an object to handle the adaptive behavior
// of the program.
AdaptEngine02 adapter = new AdaptEngine02(
adaptiveFilterLength,feedbackGain);
//Perform the specified number of iterations. This is
// the sum of the specified number of adaptive
// iterations plus the non-adaptive iterations that are
// used to compute the percent error after the adaptive
// update process is disabled.
for(int cnt = 0;
cnt < numberAdaptiveIterations + rmsAveragingLength;
cnt++){
//The following variable is used to control whether
// or not the adapt method of the adaptive engine
// updates the filter coefficients when it is called.
// The filters are updated when this variable is
// true and are not updated when this variable is
// false.
adaptOn = true;
//Get and scale the next sample of white noise data
// from a random number generator. Before scaling by
// noiseScale, the values are uniformly distributed
// from -1.0 to 1.0.
whiteNoise = noiseScale*(2*(random() - 0.5));
//Get and scale the next sample of signal. The
// signal is a pure tone with a frequency equal to
// one-eighth of the sampling frequency. Before
// scaling by signalScale, the peak-to-peak value
// is 2.
signal = signalScale * getCosine(cnt);
//Insert the signal plus white noise data into the
// delay line that will be used to convolve the
// signal plus white noise data with the bandpass
// filter.
double signalPlusNoise = whiteNoise + signal;
flowLine(whiteNoiseDelayLine,signalPlusNoise);
//Declare a variable to receive the filtered signal
// plus noise sample.
double filteredSignalPlusNoise = 0;
//Apply the bandpass filter operator to the signal
// plus white noise data. If the filter length is 1,
// bypass the filtering operation and use the raw
// signal plus white noise.
if(bpFilterOperator.length == 1){
filteredSignalPlusNoise = signalPlusNoise;
}else{
filteredSignalPlusNoise = reverseDotProduct(
whiteNoiseDelayLine,
bpFilterOperator)/(bpFilterOperator.length/2.0);
}//end else
//Insert the filtered signal plus noise into the
// delay line that is used to obtain a time-advanced
// sample of the target.
flowLine(
signalPlusNoiseDelayLine,filteredSignalPlusNoise);
//Declare a variable that will be populated with the
// results returned by the adapt method of the
// adaptive engine.
AdaptiveResult result = null;
//Disable adaptive updates when the specified number
// of adaptive iterations has been performed.
if(cnt > numberAdaptiveIterations){
adaptOn = false;
}//end if
//Establish the appropriate input values and perform
// the adaptive updates to the adaptive filter
// coefficients.
input = signalPlusNoiseDelayLine[0];//historical samp
target =
signalPlusNoiseDelayLine[predictionDistance];
result = adapter.adapt(input,target,adaptOn);
//Get and save adaptive results.
output = result.output;
err = result.err;
//Compute values that will be used later to compute
// the percent error. This computation is performed
// only after adaptive updates have been disabled.
if(!adaptOn){
//Accumulate the sum of the squares of the target
// and error values.
targetSumSq += target * target;
errSumSq += err * err;
}//end if
//Feed the time series data to the plotting object.
// Plot only two pages of data after adaptive updates
// are disabled.
if(cnt <= numberAdaptiveIterations + 2*sampPerPage){
timePlotObj.feedData(input,target,output,err);
}//end if
}//End for loop on required number of iterations.
//Compute and display the mean square values
double rmsTarget =
sqrt(targetSumSq/rmsAveragingLength);
double rmsError = sqrt(errSumSq/rmsAveragingLength);
System.out.println("\nRMS target: " + rmsTarget);
System.out.println("RMS error: " + rmsError);
System.out.println(
"Percent error: " + 100.0*(rmsError)/(rmsTarget));
//Cause the data stored in the plotting object to be
// plotted.
timePlotObj.plotData(0,296);
}//end process method
//-----------------------------------------------------//
//This method simulates a tapped delay line. It receives
// a reference to an array and a value. It discards the
// value at index 0 of the array, moves all the other
// values by one element toward 0, and inserts the new
// value at the top of the array.
void flowLine(double[] line,double val){
for(int cnt = 0;cnt < (line.length - 1);cnt++){
line[cnt] = line[cnt+1];
}//end for loop
line[line.length - 1] = val;
}//end flowLine
//-----------------------------------------------------//
void displayFreqResponse(
double[] filter,PlotALot03 plot,int len,int zeroTime){
//Create the arrays required by the Fourier Transform.
double[] timeDataIn = new double[len];
double[] realSpect = new double[len];
double[] imagSpect = new double[len];
double[] angle = new double[len];
double[] magnitude = new double[len];
//Copy the filter into the timeDataIn array
System.arraycopy(filter,0,timeDataIn,0,filter.length);
//Compute DFT of the filter from zero to the folding
// frequency and save it in the output arrays.
ForwardRealToComplex01.transform(timeDataIn,
realSpect,
imagSpect,
angle,
magnitude,
zeroTime,
0.0,
0.5);
//Find the absolute peak value. Begin with a negative
// peak value with a large magnitude and replace it
// with the largest magnitude value.
double peak = -9999999999.0;
for(int cnt = 0;cnt < magnitude.length;cnt++){
if(peak < abs(magnitude[cnt])){
peak = abs(magnitude[cnt]);
}//end if
}//end for loop
//Normalize to 20 times the peak value
for(int cnt = 0;cnt < magnitude.length;cnt++){
magnitude[cnt] = 20*magnitude[cnt]/peak;
}//end for loop
//Now feed the normalized data to the plotting
// object.
for(int cnt = 0;cnt < magnitude.length;cnt++){
plot.feedData(magnitude[cnt],angle[cnt]/20);
}//end for loop
}//end displayFreqResponse
//-----------------------------------------------------//
//This method receives two arrays and treats each array
// as a vector. The two arrays must have the same length.
// The program reverses the order of one of the vectors
// and returns the vector dot product of the two vectors.
double reverseDotProduct(double[] v1,double[] v2){
if(v1.length != v2.length){
System.out.println("reverseDotProduct");
System.out.println("Vectors must be same length.");
System.out.println("Terminating program");
System.exit(0);
}//end if
double result = 0;
for(int cnt = 0;cnt < v1.length;cnt++){
result += v1[cnt] * v2[v1.length - cnt - 1];
}//end for loop
return result;
}//end reverseDotProduct
//-----------------------------------------------------//
//This method returns the values of a cosine function
// sampled eight samples per cycle.
double getCosine(int index){
int cnt = index%8;
if(cnt == 0){
return 1.0;
}else if(cnt == 1){
return 0.7071067811865476;
}else if(cnt == 2){
return 0;
}else if(cnt == 3){
return -0.7071067811865476;
}else if(cnt == 4){
return -1.0;
}else if(cnt == 5){
return -0.7071067811865476;
}else if(cnt == 6){
return 0;
}else if(cnt == 7){
return 0.7071067811865476;
}//end else
return 0;//Make the compiler happy.
}//end getCosine
//-----------------------------------------------------//
}//end class Adapt09
|
Copyright 2006, Richard G. Baldwin. Reproduction in whole or in part in any form or medium without express written permission from Richard Baldwin is prohibited.
Richard has participated in numerous consulting projects and he frequently provides onsite training at the high-tech companies located in and around Austin, Texas. He is the author of Baldwin's Programming Tutorials, which have gained a worldwide following among experienced and aspiring programmers. He has also published articles in JavaPro magazine.
In addition to his programming expertise, Richard has many years of practical experience in Digital Signal Processing (DSP). His first job after he earned his Bachelor's degree was doing DSP in the Seismic Research Department of Texas Instruments. (TI is still a world leader in DSP.) In the following years, he applied his programming and DSP expertise to other interesting areas including sonar and underwater acoustics.
Richard holds an MSEE degree from Southern Methodist University and has many years of experience in the application of computer technology to real-world problems.
Keywords
Java adaptive filtering convolution filter frequency spectrum LMS amplitude
phase time-delay linear DSP impulse decibel log10 DFT transform bandwidth signal
noise real-time dot-product vector time-series prediction identification inverse
noise cancellation
-end-