Figure 1
Published: November 1, 2005
by Richard G. Baldwin
Java Programming Notes # 2352
DSP and adaptive filtering
With the decrease in cost and the increase in speed of digital devices, Digital Signal Processing (DSP) is showing up in everything from cell phones to hearing aids to rock concerts. Many applications of DSP are static. That is, the characteristics of the digital processor don't change with time or circumstances. However, a particularly interesting branch of DSP is adaptive filtering. This is a situation where the characteristics of the digital processor change with time, circumstances, or both.
Second in a series
This is the second lesson in a series designed to teach you about adaptive filtering in Java.
The first lesson, titled Adaptive Filtering in Java, Getting Started, introduced you to the topic by showing you how to write a Java program to adaptively design a time-delay convolution filter with a flat amplitude response and a linear phase response using an LMS adaptive algorithm. That was a relatively simple time-adaptive filtering problem for which the correct solution was well known in advance. That made it possible to check the adaptive solution against the known solution.
An adaptive whitening filter
In this lesson, I will show you how to write an adaptive whitening filter program in Java, which is conceptually more difficult than the filter that I explained in the previous lesson. This lesson will also show you how to use the whitening filter to extract wide-band signal from a channel in which the signal is corrupted by one or more components of narrow-band noise.
Viewing tip
You may find it useful to open another copy of this lesson in a separate browser window. That will make it easier for you to scroll back and forth among the different listings and figures while you are reading about them.
Supplementary material
I recommend that you also study the other lessons in my extensive collection of online Java tutorials. You will find those lessons published at Gamelan.com. However, as of the date of this writing, Gamelan doesn't maintain a consolidated index of my Java tutorial lessons, and sometimes they are difficult to locate there. You will find a consolidated index at www.DickBaldwin.com.
Review of DSP concepts
Before getting into the details of the program, I need to prepare you to understand the program by reviewing some digital signal processing (DSP) concepts with you.
Sampled time series, convolution, and frequency spectrum
First there is the matter of the spectrum of a signal as well as the concepts of convolution and sampled time series. In order to understand this program, you will first need to understand the material in the following previously-published lessons:
You will find links to all of the material listed above at Digital Signal Processing-DSP.
Data predictability
The adaptive design of the whitening filter in this lesson is based on the predictability, or lack thereof, of a time series. Predictability is a measure of the degree to which it possible to use the current sample and a set of previous samples to predict the value of the next sample.
White noise versus a single-frequency sinusoid
The two extremes of predictability are given by white noise on one hand and a single frequency sinusoid on the other.
(Recall that insofar as sampled time series are concerned, white noise is represented by a time series that is composed of equal contributions of all frequencies in the spectrum between zero and the Nyquist folding frequency, which is one-half the sampling frequency.)
Generating white noise
The easiest way to generate sampled white noise is to take the values for the samples from a random number generator. If you take a sufficiently long series of such values and perform a spectral analysis on that time series, you will find that as the length of the series approaches infinity, the spectrum approaches the ideal case of an equal contribution of energy at all frequencies.
(If that doesn't happen, then the values produced by your random number generator aren't truly random.)
Random values are uncorrelated
If the series of values produced by the random number generator is truly random, then the value of each sample is totally uncorrelated with all previous values. If there is no correlation between successive values, then it is not possible to successfully predict the next value (except through pure chance) based on a knowledge of some subset or all of the previous values.
(For example, given a true coin and given the outcome of any number of previous tosses, it is not possible to predict the next toss with a probability of success greater than one chance in two. In other words, knowing the outcome of many previous tosses doesn't improve your likelihood of correctly predicting the next toss to better than one chance in two.)
Therefore, if white noise is equivalent to a series of values produced by a random number generator, it is not possible to predict the value of a white noise sample using any number of previous samples.
A sinusoid is predictable
On the other hand, a pure single-frequency sinusoid is completely deterministic. There is nothing random about it. That is to say, given a small number of successive values from a pure sinusoid, it is easy to design a convolution filter that will process that sinusoid to produce a perfect prediction of the next value given a small set of previous values.
Predictability is inversely related to bandwidth
In the real world, signals and noise are neither pure sinusoids nor completely random. However, the narrower the bandwidth of a time series, the easier it is to predict the next value given a set of previous values. Similarly, the wider the bandwidth of a time series, the more difficult it is to predict the next value given a set of previous values. The program in this lesson will take those facts into account to adaptively design a convolution filter that will extract wide-band signals that have been corrupted by additive narrow-band noise.
Why would we want to do this?
This is not an unusual circumstance. Wide-band signals corrupted by narrow-band noise can occur in a variety of real-world situations. Some of the most common are situations in which wide-band signals are corrupted by additive reverberation noise. This can occur in a theatre, for example, where specific audio frequencies tend to reverberate due to the architecture. Another common example is an audio system that is corrupted by 60-cycle hum.
Reflection seismology
One of the earliest applications of digital whitening filters (although not necessarily adaptive) took place in the industry that searches for underground petroleum deposits using reflection seismology.
In reflection seismology, a burst of energy is "shot" into the earth where it is reflected back to the surface by the different layers in the earth. The reflected energy that arrives back at the surface is measured by sensors on the surface. The two-way travel time of the energy to and from each layer is different. Thus, the reflections from the shallow layers arrive back at the surface before the reflections from the deeper layers. The output from each sensor (or possibly each group of sensors added together) is digitized and treated as a sampled time series.
Repeat the process many times
This process is repeated over and over moving along a straight line on the surface of the earth. Then the sampled time series are plotted on the same display with equal spacing between the "traces" as they are often called. Each trace represents a point on the surface of the earth, and the peaks and valleys in the time series represent reflections from the various layers in the earth below that point.
Orient the display
If this display is then oriented such that the zero time reference is at the top of the display and time increases going down the display, the peaks and valleys on the individual traces can be correlated by eye to trace out the layering in the earth. Examples of such displays are shown in Figure 2 at the following URL:
http://sepwww.stanford.edu/sep/prof/iei/mltp/paper_html/node4.html
Each of the panels in Figure 2 at the above URL consists of hundreds of seismic traces with time going down the page. To the trained eye, the layering in the earth is evident in those images.
Initially used on shore
Reflection seismology was first used to search for underground petroleum deposits underneath the land masses on the earth. In this case, the shot of energy often consisted of a small explosion with the explosive material being tamped into a shallow borehole in the earth. The sensors for each different shot point were often placed on the surface of the earth in a line.
Moving offshore
Around the turn of the twentieth century, this technique was moved offshore to those portions of the earth covered with shallow water along the continental shelves. The purpose was to find underground petroleum deposits under these shallow water areas. In this case, the sensors were often trailed along behind the boat on a cable that was slightly submerged. The shots consisted of a variety of acoustic energy sources such as small explosions, or the release of a burst of air into the water from a high-pressure pneumatic device.
Reverberation
A special new problem was encountered with the transition to offshore exploration. When the shot was fired in an attempt to inject energy into the earth, a large percentage of the energy became trapped in the water layer and continued to bounce back and forth between the surface of the water and the surface of the earth below the water. This is a form of narrow-band reverberation.
The level of the reverberation energy was greater than the level of the reflections from the deep layering of the earth. Thus, the reverberation energy appeared as narrow-band reverberation noise in the output from the sensors, and the reflection energy of interest appeared as wide-band signals. The reverberation energy tended to mask the reflections from the different surfaces in the earth making it difficult to interpret the results.
Mathematical solutions
Different mathematical techniques (usually involving matrix inversions) were used to design convolution filters that could be used to filter out the narrow-band noise and to make the wide-band signals visible in the displays. These filters were called whitening filters, and the overall process was often referred to as deconvolution.
If you are interested in learning more about the reverberation problem and deconvolution in exploration seismology, visit this site or go to Google and search for the keywords seismic and deconvolution.
An adaptive solution
The adaptive algorithm that I will present in this lesson is an adaptive approach to the matrix inversion solutions that were frequently used to solve this reverberation problem.
The algorithm is also appropriate for use in a variety of other application areas involving wide-band signals corrupted by narrow-band noise.
Before getting into the details of the program, I am going to present and explain some experimental results that were produced using the program.
How does it work?
In the previous lesson, you learned how to use a least mean square (LMS) adaptive algorithm to adjust the individual coefficients in a convolution filter. The setup was such that when the filter was applied to one sampled time series it would attempt to cause the output to look like another sampled time series.
In the scenario presented in the previous lesson, the second sampled time series was simply a time-shifted version of the first time series. As a result, the convolution filter that resulted from the adaptive process was a filter with a flat amplitude response and a linear phase response. When the filter was applied to the first sampled time series, the output was a time-shifted version of that time series that matched the second time series.
We will use that same approach in this lesson, but will apply the approach to a different scenario.
The scenario for this lesson
In this lesson, we will have a sampled time series that consists of the sum of unpredictable wide-band signal and narrow-band (predictable) noise. The objective is to produce a replica of the narrow-band noise and then to subtract it from the original time series consisting of signal plus noise. If successful, this will produce an output consisting mainly of the original wide-band signal.
Will predict the next sample in the series
We will set the adaptive algorithm up so that it uses the current sample plus a specified number of history samples to develop a convolution filter that is capable of predicting the value of the next sample.
Because the narrow-band noise is largely predictable and the wide-band signal is largely unpredictable, the filter coefficients will adjust themselves to make a good prediction of the narrow-band noise. When we apply this convolution filter to the time series consisting of signal plus noise, the output will be an estimate of the waveform of the narrow-band noise. We will then subtract that waveform from the time series consisting of signal plus noise, leaving an estimate of the wide-band signal.
The quality of the results
The quality of the estimate of the wide-band signal will depend on a variety of factors including but not limited to:
Some experiments
Before getting into the details regarding the program code, we will perform some experiments where we will vary the factors in the above list and observe the results.
First, however, I want to discuss of the difference between a prediction filter and a whitening filter, and to introduce you to the graphic output produced by the program.
The whitening process
In the above discussion, I explained that we will develop a convolution filter that can be applied to a sampled time series consisting of signal plus noise to use the current sample plus a specified number of historical samples to produce an output value that is an estimate of the value of the next sample.
I also explained that in order to separate the signal from the noise, we will subtract the estimate of the next sample from the actual value of the next sample. The combined process of applying the prediction filter and performing the subtraction process can be thought of as a whitening processing.
The whitening filter
I hope that by now you are sufficiently familiar with the convolution process that you will recognize that we can combine these two steps simply by concatenating a coefficient value of -1 onto the end of the prediction filter and applying this filter to the sampled time series consisting of signal plus noise.
I will refer to the filter that is created by concatenating a coefficient with a value of -1 onto the prediction filter as the whitening filter. I will show you an example of a whitening filter shortly.
The time-series output
This program uses a class named PlotALot07 to display various sampled time series involved in the adaptive process.
(In fact, much of the code in this program involves displaying various results for explanation purposes having nothing to do with the actual adaptive process.)
PlotALot07
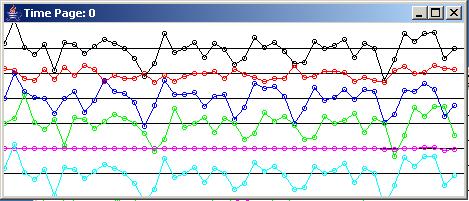
An object of the PlotALot07 class produces multiple pages of plotted data with multiple traces or time series on each page. Figure 1 shows an example of one of the pages produced by this program.
Figure 1 |
Each page displays six different sampled time series plotted horizontally with time increasing from left to right. (At this point, I will start referring to the sampled time series as traces.)
Figure 1 shows the page produced by the program at the beginning of an adaptive run for a specific set of parameters.
The output from the whitening filter
The black trace at the top of Figure 1 shows the output from the whitening filter. Ideally this trace contains the wide-band signal with the narrow-band noise having been removed. However, in Figure 1, the top trace is still significantly corrupted by the narrow-band noise.
Figure 2 shows the graphic output produced by the same run after approximately 500 adaptive iterations. At this point, the narrow-band noise has been largely removed by the application of the whitening filter leaving only the wide-band signal in the top trace in Figure 2.
Figure 2 |
The wide-band signal
The second (red) trace in Figure 1 and Figure 2 shows the raw wide-band signal prior to adding the narrow-band noise. This wide-band signal consists of samples taken from a random number generator. Therefore, this is a white signal containing equal contributions of all frequency components between zero and the Nyquist folding frequency.
Ideally, the top trace should look exactly like the second trace once the narrow-band noise has been removed. This is pretty much the case after 500 adaptive iterations in Figure 2.
The narrow-band noise
The third (blue) trace in Figure 1 and Figure 2 shows the narrow-band noise that was added to the wide-band signal for the purpose of purposely corrupting the signal. For the case shown in Figure 1 and Figure 2, the narrow-band noise consisted of a single sinusoid with a peak-to-peak amplitude roughly twice the peak-to-peak amplitude of the wide-band signal.
The wide-band signal plus the narrow-band noise
The fourth (green) trace in Figure 1 and Figure 2 shows the sum of the wide-band signal and the narrow-band noise. This is the time series that is processed by the whitening filter to produce the output shown in the top trace.
You might note that at the beginning of the adaptive run in Figure 1, the output of the whitening filter in the top trace is very similar to the fourth trace except for a time shift. However, by the end of 500 adaptive iterations, the output from the whitening filter bears little resemblance to the fourth trace, but instead looks much more like the second trace, which is pure signal.
Output from the prediction filter
The output from the fifth (violet) trace is the output produced by applying the prediction filter to the fourth trace consisting of the sum of signal and noise. At the beginning of the adaptive process in Figure 1, the output from the prediction filter is essentially zero for all output values. (This is because all of the initial coefficients in the prediction filter were initialized to a value of zero.) However, by the end of 500 adaptive iterations, the output from the prediction filter in the fifth trace is a very good replica of the narrow-band noise in the third trace. Thus, subtracting the prediction filter output from the input that consists of the sum of signal and noise leaves a good estimate of the signal.
The adaptive target
The sixth trace at the bottom is the target time series that is used
to control the
adaptive process.
(I explained the use of an adaptive target in the previous lesson.)
This trace displays the next sample beyond the samples that are processed by the prediction filter during each adaptive iteration. This trace is essentially the signal plus noise with a time shift as you can see by comparing it to the fourth (green) trace in Figure 1 and Figure 2. The prediction filter attempts to predict the value of this trace during each iteration and the adaptive process is designed to improve the ability of the prediction filter to perform that prediction in a high quality fashion.
The impulse response and the frequency response
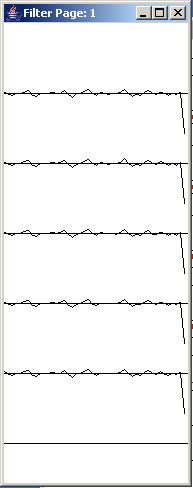
As another approach to explaining how adaptive whitening works, Figure 3 shows the impulse response and the frequency response of the whitening filter at the beginning of the run, and at the end of every 100 iterations of the iterative adaptive process.
The impulse responses of the whitening filters at those points in time are shown in the panel on the left of Figure 3. The frequency response of each of the impulse responses is shown in the panel on the right of Figure 3.
 |
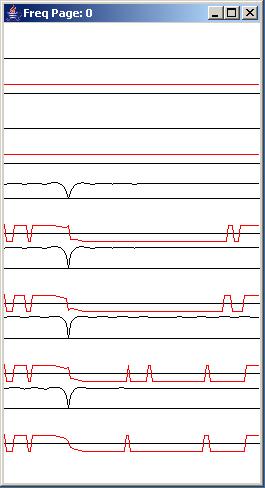 |
Figure 3 |
|
The impulse response of the whitening filter
First consider the impulse response of the whitening filter. The top trace in the left panel shows the impulse response at the beginning of the run before the adaptive process begins. Each of the traces below that one shows the impulse response at the end of each set of 100 adaptive iterations, ending with the impulse response at the end of 500 iterations.
The impulse response of the whitening filter always ends with a coefficient value of -1.
(Recall that the whitening filter is constructed by concatenating a coefficient with a value of -1 onto the end of the prediction filter.)
The impulse response of the prediction filter
Thus, the impulse response of the prediction filter consists of all of the coefficient values to the left of the coefficient having the value of -1. These coefficient values are initialized to values of zero at the beginning of the adaptive process as shown by the top impulse response in Figure 3.
As you can see by examining each impulse response going down the page, the adaptive process causes the prediction filter coefficients to take on different values as the adaptive process proceeds through 500 adaptive iterations.
As you can also see, the coefficient values for the prediction filter have pretty well stabilized by the end of 300 iterations for this set of conditions.
The frequency response
Although the format can be a little confusing, the right panel in Figure 3 shows the amplitude and phase response of each of the whitening filters shown in the left panel. Each of the plots in the right panel shows the frequency response from a frequency of zero on the left, to the Nyquist folding frequency (one-half the sampling frequency) on the right.
The red and black traces
To get your bearings, consider the red trace and the black trace at the bottom of the right panel. The black trace with the notch near the bottom of the right panel shows the amplitude response of the whitening filter in the bottom of the left panel. The red trace at the bottom of the right panel shows the corresponding phase response for the same whitening filter plotted over an interval of +180 degrees to -180 degrees.
Each such pair of red and black traces corresponds to the phase and amplitude response of the whitening filter immediately to the left of the red phase response.
A notch filter
Consider first the amplitude response shown by the black trace at the bottom of the right panel. This amplitude response shows a reasonably sharp notch at a frequency about one fourth of the way between zero on the left and the Nyquist folding frequency on the right. The location of the notch matches the frequency of the narrow-band noise that was suppressed by the adaptive process.
A flat wide-band response
The frequency response of the whitening filter is relatively flat at all frequencies on both sides of the notch. When this filter is applied to the input consisting of wide-band signal plus narrow-band noise at the same frequency as the notch, the filter does a reasonably good job of preserving the wide-band signal and suppressing the narrow-band noise. That agrees with what we saw in the time series output in Figure 2.
The adaptive progression
If you examine the amplitude response curves at each level from top to bottom, you can see how this notch develops as the adaptive process converges. As was the case with the impulse response, the position of the notch and the flatness at surrounding frequencies was pretty well established and stabilized by the end of about 300 adaptive iterations.
The phase response
Another important characteristic of the whitening filter is the phase response. The output of a filter with a flat amplitude response and a phase shift of zero degrees simply reproduces the input. That is probably the best case scenario. A phase shift of 180 degrees (or -180 degrees) reverses the algebraic sign of the input values. This is probably the next best scenario because this phase shift is relatively easy to compensate for.
(Note that a -180-degree phase shift is the same as a +180-degree phase shift.)
Phase or waveform distortion
Except for the unique case of a linear phase shift (see the previous lesson), phase shifts between the two extremes of zero degrees and 180 degrees usually introduce phase or waveform distortion into the signal. This is usually undesirable and can be difficult to compensate for.
The phase response curve
The red phase response curves in Figure 3 are plotted against a black axis that represents zero degrees. As you can see, at the end of 500 adaptive iterations and at most frequencies, the phase shift is either +180 degrees or -180 degrees, indicating that there will be very little phase or waveform distortion in the signal as it passes through the whitening filter. The only frequencies where this is not true is in the narrow band of frequencies in the near vicinity of the notch in the amplitude response. Thus, we can expect a small amount of phase distortion for those signal components on either side of the notch in the amplitude response.
Overall, as we saw in Figure 2, this whitening filter does a reasonably good job of suppressing the narrow-band noise while preserving the wide-band signal with very little phase or waveform distortion.
Required input data
The user is required to provide the information shown in Figure 4 as command-line parameters to the program.
(If the user fails to provide the required command-line parameters, default values are used. The results shown in Figures 1 through 3 resulted from the default values.)
feedbackGain: The gain factor that is used in the feedback loop to adjust the coefficient values in the prediction/whitening filter. (A whitening filter is a prediction filter with a -1 appended to its end.) If the value of the feedbackGain is too high, the program will become unstable. If too low, convergence will take a long time. Values toward the low end tend to converge to better solutions. It is possible for the feedbackGain value to be low enough to avoid instability but high enough to cause the adaptive process to bounce around and never find a good solution. Typical useful values for feedbackGain in this program are around 0.00001. numberIterations: The is the number of iterations that the program executes before stopping and displaying all of the graphic results. predictionFilterLength: This is the number of coefficients in the prediction filter. This can be any integer value greater than zero. The program will throw an exception if this value is zero. Typical values are 15 to 30. Longer filters tend to produce better results in terms of the narrowness of the notches at the noise frequencies and the flatness of the filter between the notches. signalScale: A scale factor that is applied to the wide band signal provided by the random noise generator. The random noise generator produces uniformly distributed values ranging from -0.5 to +0.5. Scaling values of from 10 to 20 work well in terms of producing a wide-band signal that is of a suitable magnitude for plotting. Set this to 0 to see how the program behaves in the presence of noise and the absence of signal. noiseScale: A scale factor that is applied to each of the sinusoidal noise functions before they are added to the signal. The raw sinusoids vary from -1.0 to +1.0. Scaling values of from 10 to 20 work well in terms of being of a suitable magnitude for plotting. Set this to 0 to see how the program behaves in the presence of wide-band signal and the absence of narrow-band noise. numberNoiseSources: This value specifies the number of sinusoidal noise components that are added to the wide-band signal. Must be an integer value from 0 to 3. Figure 4 |
The default values
For the record, the default values that produced the output shown in Figures 1 through 3 are as shown in Figure 5.
Using following values by default: feedbackGain: 1.0E-5 numberIterations: 500 predictionFilterLength: 26 signalScale: 20.0 noiseScale: 20.0 numberNoiseSources: 1 Figure 5 |
A more difficult problem
Now let's look at the experimental results for a considerably more difficult scenario. The parameters for this scenario are shown in Figure 6.
Using following values from input: feedbackGain: 1.0E-5 numberIterations: 1000 predictionFilterLength: 45 signalScale: 20.0 noiseScale: 10.0 numberNoiseSources: 3 Figure 6 |
The main thing that makes this scenario more difficult is the fact that there are three narrow-band noise components instead of only one. This means that the adaptive process will be required to build a whitening filter with a frequency response that has three notches but which is otherwise flat.
To accommodate this added difficulty, I increased the prediction filter length to 45 coefficients and extended the number of adaptive iterations from 500 to1000. I didn't change the feedback gain.
The time-domain output
Figure 7 shows the time-domain graphs at the beginning and at the end of the adaptive run after 1000 adaptive iterations.
|
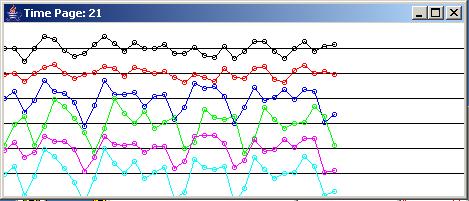 |
Figure 7 |
As you can see in the bottom panel of Figure 7, the whitening filter output in the top (black) trace is a reasonably good representation of the actual wide-band signal shown in the second (red) trace. This indicates that the adaptive process was successful in designing a whitening filter that suppresses the three narrow-band noise components while preserving the wide-band signal.
The impulse response and the frequency response
Figures 8 and 9 show the impulse and frequency response curves for the whitening filter as the adaptive process converges. The traces at the top of Figure 8 show the impulse response and frequency response of the whitening filter before the adaptive process began. Each successive set of traces shows the response curves at the end of 100 adaptive iterations.
 |
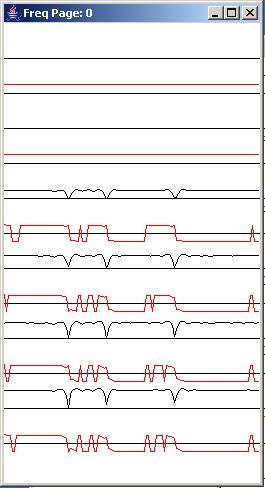 |
Figure 8 |
|
The traces at the bottom of Figure 8 show the response curves after 500 adaptive iterations.
 |
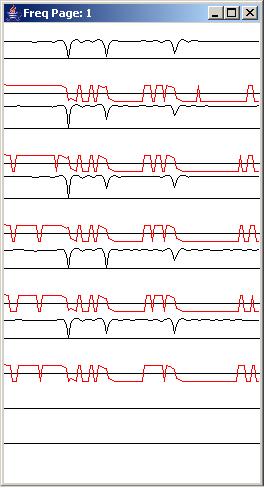 |
Figure 9 |
|
The fifth set of traces down from the top in Figure 9 show the response curves at the end of 1000 iterations.
Three notches are visible
You can see the three notches in the frequency response develop as you examine the curves from the top of Figure 8 to near the bottom of Figure 9.
Reasonably flat amplitude response
Although some ripple is evident in the amplitude response near the bottom of Figure 9, the amplitude response outside the areas of the three notches is reasonably flat.
Well-behaved phase response
Also, outside the areas of the three notches, the phase response is very close to either 180 degrees or -180 degrees indicating that there should be very little phase or waveform distortion for the wide-band signal. This agrees with a visual comparison of the first and second traces in the bottom panel of Figure 7.
Enough talk, let's see some code
Now that you know what to expect from the behavior of this program, it's time to examine the program code in some detail.
The program named Adapt02 illustrates one aspect of time-adaptive signal processing. This program implements a time-adaptive whitening filter using a predictive approach.
Input signal plus noise
The program input is a time series consisting of a wide-band signal plus up to three sinusoidal noise components. The program adaptively creates a filter that attempts to eliminate the sinusoidal noise while preserving the wide-band signal.
Time series output
The following time series are displayed when the program runs:
Examples of these six sampled time series outputs are shown in Figure 1 and Figure 2 above.
Frequency response of the whitening filter
Although not required by the adaptive process, the frequency response of the whitening filter is computed and displayed once every 100 adaptive iterations. This output is provided to help you to understand the adaptive process.
Ideally the amplitude response will be flat with very narrow notches at the frequencies of the interfering sinusoidal noise components.
Both the amplitude and the phase response are displayed once every 100 iterations. This makes it possible for you to see the notches develop in the frequency response of the whitening filter as it converges on a solution. It also makes it possible for you to see how the phase behaves at and between the notches in the amplitude response.
An example of the frequency response output is shown in the right panel in Figure 3 above.
Impulse response of the whitening filter
The individual time-domain whitening filters, (on which the frequency response is computed), are also displayed once every 100 iterations. An example is shown in the left panel of Figure 3.
Command-line input
The user provides six command line parameters to control the operation of the program. These command-line parameters are described in Figure 4 above. If the user doesn't provide any command line parameters, six default values are used instead.
In addition to the class named Adapt02, this program requires the following classes:
I provided the source code for and explained the class named PlotALot01 in the earlier lesson titled Plotting Large Quantities of Data using Java. Therefore, I won't repeat that explanation in this lesson.
I also provided and explained the class named PlotALot03 in the earlier lesson titled Plotting Large Quantities of Data using Java, and I won't repeat that material here either.
I provided the source code for and explained the class named ForwardRealToComplex01 in the earlier lesson titled Spectrum Analysis using Java, Sampling Frequency, Folding Frequency, and the FFT Algorithm. Once again, I will simply refer you to that lesson and won't repeat that material here.
The class named PlotALot07 is new to this lesson. The source code for this class is provided in Listing 22 near the end of the lesson. The class named PlotALot07 is a simple extension of the class named PlotALot04, which I explained in the lesson titled Plotting Large Quantities of Data using Java. I will refer you to that lesson for a general explanation of the class and won't provide further explanation of the class named PlotALot07.
Program testing
This program was tested using J2SE 5.0 running under Windows XP. J2SE 5.0 or later is required due to the use of Generics and the use of static import directives.
The beginning of the class named Adapt02 and the beginning of the main method is shown in Listing 1.
class Adapt02{
public static void main(String[] args){
//Default parameter values
double feedbackGain = 0.00001;
int numberIterations = 500;
int predictionFilterLength = 26;
double signalScale = 20;
double noiseScale = 20;
int numberNoiseSources = 1;
|
The code in Listing 1 establishes default values for six program parameters. These default values are used if the user doesn't provide six parameters on the command line. These default values were used to produce the program outputs shown in Figure 1 through Figure 3.
Dealing with the command-line parameters
The code in Listing 2 deal with the command-line parameters as described above.
if(args.length != 6){
System.out.println(
"Usage with all parameters following " +
"program name:\n" +
"java Adapt02\n" +
"feedbackGain\n" +
"numberIterations\n" +
"predictionFilterLength\n" +
"signalScale\n" +
"noiseScale\n" +
"numberNoiseSources\n");
System.out.println(
"Using following values by default:\n" +
"feedbackGain: " + feedbackGain +
"\nnumberIterations: " + numberIterations +
"\npredictionFilterLength: " +
predictionFilterLength +
"\nsignalScale: " + signalScale +
"\nnoiseScale: " + noiseScale +
"\nnumberNoiseSources: " + numberNoiseSources);
}else{//Command line params were provided.
feedbackGain = Double.parseDouble(args[0]);
numberIterations = Integer.parseInt(args[1]);
predictionFilterLength = Integer.parseInt(args[2]);
signalScale = Double.parseDouble(args[3]);
noiseScale = Double.parseDouble(args[4]);
numberNoiseSources = Integer.parseInt(args[5]);
System.out.println(
"Using following values from input:\n" +
"feedbackGain: " + feedbackGain +
"\nnumberIterations: " + numberIterations +
"\npredictionFilterLength: " +
predictionFilterLength +
"\nsignalScale: " + signalScale +
"\nnoiseScale: " + noiseScale +
"\nnumberNoiseSources: " + numberNoiseSources);
}//end else
|
The code in Listing 2 also displays the parameters that are used for each run of the program on the command-line screen.
The code in Listing 2 is straightforward and shouldn't require further explanation.
Invoke the method named process
The code in Listing 3 instantiates a new object of the Adapt02 class and invokes the method named process on that object. The values of each of the six command-line parameters described above are passed to the process method. These values have already been converted from command-line String objects to values of type double and type int.
new Adapt02().process(feedbackGain,
numberIterations,
predictionFilterLength,
signalScale,
noiseScale,
numberNoiseSources);
}//end main
|
Listing 3 also signals the end of the main method. When the process method returns, the program terminates.
The process method
Listing 4 shows the beginning of the method named process. This is the primary adaptive processing and plotting method for the program.
void process(double feedbackGain,
int numberIterations,
int predictionFilterLength,
double signalScale,
double noiseScale,
int numberNoiseSources){
|
The initial prediction filter
Listing 5 creates the initial prediction filter with a value of zero for every coefficient. The coefficient values are stored as values of type double in an array object referred to by predictionFilter. Recall that array elements of type double are automatically initialized to a value of zero in Java.
double[] predictionFilter =
new double[predictionFilterLength];
|
You could easily initialize the coefficient values in the prediction filter to values other than zero if you had a reason to do so.
The initial whitening filter
The code in Listing 6 creates the initial whitening filter and initializes it for spectrum analysis and plotting by:
double[] whiteningFilter =
new double[predictionFilter.length + 1];
System.arraycopy(predictionFilter,
0,
whiteningFilter,
0,
predictionFilter.length);
//Set the final value in the whitening filter to -1.
whiteningFilter[whiteningFilter.length - 1] = -1;
|
Create two delay lines
The code in Listing 7 creates two array objects to serve as delay lines. The previous lesson taught you about delay lines, so I won't repeat that material here.
//Create an array to serve as a two-sample delay line
// for the raw data.
double[] rawData = new double[2];
//Create an array to serve as a processing delay line
// for the data being processed.
double[] chanA = new double[predictionFilter.length];
|
Plotting objects
Listing 8 instantiates an object of the PlotALot07 class, which is used later to plot the time series data shown in Figure 1 and Figure 2.
PlotALot07 timePlotObj =
new PlotALot07("Time",468,200,25,10,4,4);
PlotALot03 freqPlotObj =
new PlotALot03("Freq",264,487,35,2,0,0);
PlotALot01 filterPlotObj = new PlotALot01("Filter",
(whiteningFilter.length * 4) + 8,487,70,4,0,0);
|
Then Listing 8 instantiates an object of the PlotALot03 class, which is used later for plotting two channels of frequency response data at specific time intervals during the adaptive process as shown in the right panel of Figure 3. One channel is for the amplitude response and the other channel is for the phase response.
Finally, Listing 8 instantiates an object of the PlotALot01 class, which is used later to display the whitening filter at specific time intervals during the adaptive process as shown in the left panel of Figure 3.
If you have been following along and reading my previous lessons, the use of objects from the PlotALot family of classes should be very familiar to you by now. Therefore, I won't discuss this topic further in this lesson.
A possible point of confusion
There is one possible point of confusion, however, that is worth noting in this lesson (although it was explained fully in the previous lesson).
The minimum allowable width for a Java Frame object is 112 pixels when Java is running under Windows XP. Therefore, the display of the impulse responses of the whitening filters won't synchronize properly and show one filter on each line for whitening filter lengths less than 26 coefficients. To compensate for this problem, the code that feeds data to the plotting object later in the program extends the length of the filter to cause it to synchronize and to plot one set of filter coefficients on each line.
The value of the extension coefficients
When the filter is artificially extended (for plotting purposes only), it is extended with artificial filter coefficients having a value of 2.5. This was done to make it obvious which part of the plot shows the actual filter coefficients and which part shows the artificial extension.
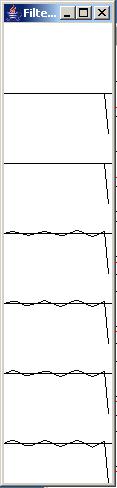
Figure 10 shows the display of a six whitening filters based on a prediction filter length of only fifteen coefficients.
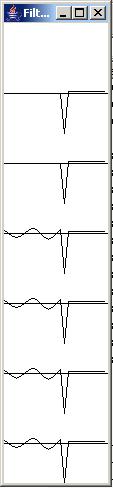 Figure 10 |
The flat raised portion on the right side of each individual impulse response is not part of the actual filter, but rather is the artificial extension that was necessary to force this plot to synchronize properly under Windows XP. The result of proper synchronization is that the impulse responses are plotted one above the other as shown. (If this seems confusing, I recommend that you read more about it in the previous lesson.)
Working variables
Listing 9 declares and initializes several working variables.
//Declare and initialize working variables.
double output = 0;
double err = 0;
double target = 0;
double input = 0;
double signal = 0;
double sineNoise = 0;
|
Display the frequency response
Recall that the adaptive process hasn't begun at this point in the program. Listing 10 invokes the method named displayFreqResponse to display the frequency response of the initial whitening filter in the top of the right panel in Figure 3.
displayFreqResponse(whiteningFilter,freqPlotObj,128,
whiteningFilter.length - 1);
|
At this point, the whitening convolution filter consists of a single coefficient with a value of -1. All other coefficients have a value of zero. As would be expected, therefore, the amplitude response is flat across the entire frequency spectrum. The phase response is also flat across the entire spectrum with a value of 180 degrees.
(For the record, the frequency response is computed at 128 points between zero and the Nyquist folding frequency.)
The method named displayFreqResponse was explained in detail in the previous lesson, so I won't repeat that material here.
Display the initial whitening filter
Listing 11 displays the initial whitening filter at the top of the left panel in Figure 3 by feeding the filter coefficients to the plotting object instantiated earlier and referred to by filterPlotObj.
for(int cnt = 0;cnt < whiteningFilter.length;cnt++){
filterPlotObj.feedData(40*whiteningFilter[cnt]);
}//end for loop
//Extend the whitening filter with a value of 2.5 for
// display purposes only if it is too short to
// synchronize properly with the plotting software.
// This value of 2.5 is easily recognizable in the
// plot as artificial extended data. See earlier
// comment on this topic.
//Note that this approach to forcing synchronization
// will not cause the plot to synchronize properly on
// an operating system for which the sum of the left
// and right insets on a Frame object are different
// from 8 pixels. The same approach to synchronization
// could be used but the minimum synchronizable filter
// length would probably be different.
if(whiteningFilter.length <= 26){
for(int cnt = 0;cnt < (26 - whiteningFilter.length);
cnt++){
filterPlotObj.feedData(2.5);
}//end for loop
}//end if
|
If the length of the whitening filter is less than or equal to 26 coefficients, the code in Listing 11 extends the filter for plotting purposes as described earlier.
(If you are running this program under some operating system other than Windows XP, the plot may not synchronize properly under your operating system. In that case, you should pay particular attention to the comments in Listing 11.)
Create the test data
We are now ready to execute the for loop that is used to implement the iterative adaptive process.
During each iteration of the for loop, the code in Listing 12 generates one sample of wide-band signal by getting a value from a random number generator. Then it creates a sample of narrow-band noise by getting and adding one, two, or three values from the sin method of the Math class. The signal sample and the noise sample are both scaled by factors provided by the user.
for(int cnt = 0;cnt < numberIterations;cnt++){
//Get the next sample of wideband signal.
signal = signalScale*(Math.random() - 0.5);
//Get the next sample of sinusoidal noise containing
// three, two, or one sinusoid.
if(numberNoiseSources == 3){
sineNoise = noiseScale*(Math.sin(2*cnt*PI/8) +
Math.sin(2*cnt*PI/5) +
Math.sin(2*cnt*PI/3));
}else if(numberNoiseSources == 2){
sineNoise = noiseScale*(Math.sin(2*cnt*PI/8) +
Math.sin(2*cnt*PI/5));
}else if(numberNoiseSources == 1){
sineNoise = noiseScale*(Math.sin(2*cnt*PI/8));
}else{
System.out.println(
"Incorrect number noise sources, terminating");
System.exit(0);
}//end else
|
Add the signal to the noise
Listing 13 adds the signal to the noise and passes the sum to the method named flowLine for insertion into the delay line referred to by rawData.
flowLine(rawData,signal + sineNoise); |
The method named flowLine was explained in detail in the previous lesson, so I won't repeat that explanation here.
Populate the chanA delay line
Listing 14 populates the chanA delay line with the next to the last value in the rawData delay line. The last sample value in the rawData delay line will be the adaptive target.
flowLine(chanA,rawData[rawData.length - 2]); |
Get and save data for plotting
Listing 15 gets the most recent sample that was put into the chanA delay line and saves it for plotting.
input = chanA[chanA.length -1]; |
Apply the prediction filter
Listing 16 invokes the dotProduct method to apply the coefficients belonging to the prediction filter to the data samples contained in the chanA delay line.
(Click here to read a description of a vector dot product from Mathworld. The vector dot product is a central element in the computational process involved in convolution.)
output = dotProduct(predictionFilter,chanA); |
I explained the dotProduct method in detail in the previous lesson and won't repeat that explanation here.
Compute the prediction error
Listing 17 computes the prediction error by:
//Get the signal plus noise sample from the end of
// the raw data delay line for an adaptive target.
target = rawData[rawData.length - 1];
//Compute the error between the current filter output
// and the target.
err = output - target;
|
(Note: If it weren't for the fact that I wrote this program to save and display various computational results, I could have written this code in a much more compact form involving the dot product of the whitening filter, instead of the prediction filter, and the raw data.)
Update the prediction filter coefficients
Listing 18 uses the value of the error along with the value of feedbackGain to update each of the coefficient values in the prediction filter. This is an implementation of a least mean square (LMS) adaptive algorithm.
for(int ctr = 0;ctr < predictionFilter.length;ctr++){
predictionFilter[ctr] -=
err*chanA[ctr]*feedbackGain;
}//end for loop.
|
As I mentioned in the previous lesson, I'm not going to attempt to justify this adaptive algorithm theoretically. There are hundreds of articles on the web that provide such justification. If you are interested in a justification, I recommend that you use Google to search them out and read them. For example, you might search for the keywords LMS Adaptive Algorithm or for the keywords Steepest Descent.
The code in Listing 18 signals the end of the adaptive process. Some of the code prior to this point, and most of the code following this point exists for display purposes only.
Plotting code
Listing 19 contains all of the remaining code in the for loop that began in Listing 12.
//Feed the time series data to the plotting object.
timePlotObj.feedData(
-err,signal,sineNoise,input,output,target);
//Compute and plot the frequency response and plot
// the whitening filter every 100 iterations.
if(cnt%100 == 0){
//Create a whitening filter from the data in the
// prediction filter. Begin by copying the
// prediction filter into the bottom elements of
// the whitening filter.
System.arraycopy(predictionFilter,
0,
whiteningFilter,
0,
predictionFilter.length);
//Now set the final value in the whitening filter
// to -1. A whitening filter is a prediction filter
// with a -1 appended to its end.
whiteningFilter[whiteningFilter.length - 1] = -1;
displayFreqResponse(whiteningFilter,freqPlotObj,
128,whiteningFilter.length - 1);
//Display the whitening filter coefficient values.
for(int ctr = 0;ctr < whiteningFilter.length;
ctr++){
filterPlotObj.feedData(40*whiteningFilter[ctr]);
}//end for loop
//Extend the whitening filter with a value of 2.5
// for plotting if necessary to cause it to
// synchronize with one filter on each axis.
// See explanatory comment earlier.
if(whiteningFilter.length <= 26){
for(int count = 0;
count < (26-whiteningFilter.length);count++){
filterPlotObj.feedData(2.5);
}//End for loop
}//End if statement
}//End display of frequency response and whitening
// filter
}//End for loop, End adaptive process
|
As mentioned earlier, the code in Listing 19 is mainly used for display purposes. This code is straightforward and shouldn't require further explanation.
Cause the data to be plotted
The code in Listing 20 causes all of the data that has been fed to the plotting objects during the running of the program to actually be plotted on the screen.
timePlotObj.plotData();
freqPlotObj.plotData(0,201);
filterPlotObj.plotData(265,201);
}//end process method
|
Listing 20 also signals the end of the method named process.
The adaptive process
The actual adaptive process is mainly executed in Listing 16, Listing 17, and Listing 18, plus those listings that involve feeding signal plus noise data into the delay lines. Thus, the bulk of the code in this program is used for the following purposes having little or nothing to do with the adaptive process:
If that code were to be eliminated from the program, leaving only the code
required by the adaptive process, this would be a rather short and compact
program.
I encourage you to copy the code from Listing 21 and Listing 22 into your text editor, compile it, and execute it.
Recall that you will also need to create class files for the following classes:
Earlier in this lesson, I provided links to the previously-published lessons where you can get the source code for those classes.
Experiment with the code in the class named Adapt02, making changes, and observing the results of your changes. For example, much of the code in this lesson is superfluous to the actual adaptive process, but instead is used to display data that helps to explain the adaptive process. See how much of that code you can eliminate and still have a viable program.
Separate the remaining code into two major sections. Include the code that is required to create the synthetic data for test purposes in one section. Include only the code that is required to adaptively process the data in the other section. Compare the size of the two sections in order to get a feel for the amount of code that is actually required to implement adaptive whitening filters.
In this lesson, I showed you how to write an adaptive whitening filter program in Java. I also showed you how to use the whitening filter to extract wide-band signal that is corrupted by one or more components of narrow-band noise.
The next lesson in this series will teach you how to write an adaptive line tracking program in Java.
/*File Adapt02.java
Copyright 2005, R.G.Baldwin
This program illustrates one aspect of time-adaptive signal
processing.
This program implements a time-adaptive whitening filter
using a predictive approach. The program input is a time
series consisting of a wide-band signal plus up to three
sinusoidal noise functions. The program adaptively creates
a filter that attempts to eliminate the sinusoidal noise
while preserving the wide-band signal.
The following time series are displayed when the program
runs:
-err: This is the negative of the error which is actually
the output from the whitening filter. Ideally this time
series contains the wide-band signal with the sinusoidal
noise having been removed.
signal: The raw wideband signal containing samples taken
from a random noise generator.
sineNoise: The raw noise consisting of the sum of one, two,
or three sinusoidal functions.
input: The sum of the signal plus the sinusoidal noise.
output: The output produced by applying the prediction
filter to the input signal plus noise.
target: The target signal that is used to control the
adaptive process. This is the next sample beyond the
samples that are processed by the prediction filter. In
other words, the prediction filter attempts to predict this
value. Thus, the adaptive process attempts to cause the
output from the prediction filter to match the next sample
in the incoming signal plus noise. This is an attempt to
predict a future value based solely on the current and past
values.
Although not required by the adaptive process, the
frequency response of the whitening filter is computed and
displayed once every 100 iterations. Ideally the amplitude
response is flat with very narrow notches at the
frequencies of the interfering sinusoidal noise components.
Both the amplitude and phase response are displayed. This
makes it possible to see the notches develop in the
frequency response of the whitening filter as it converges.
It also makes it possible to see how the phase behaves at
the notches.
The individual whitening filters on which the frequency
response is computed are also displayed as time series.
USAGE: The user provides six command line parameters to
control the operation of the program. If the user doesn't
provide any command line parameters, six default values are
used instead.
The command line parameters are:
feedbackGain: The gain factor that is used in the feedback
loop to adjust the coefficient values in the
prediction/whitening filter. (A whitening filter is a
prediction filter with a -1 appended to its end.) If the
value of the feedbackGain is too high, the program will
become unstable. If too low, convergence will take a long
time. Values toward the low end tend to converge to better
solutions. It is possible for the feedbackGain value to be
low enough to avoid instability but high enough to cause
the adaptive process to bounce around and never find a good
solution. Typical useful values for feedbackGain in this
program are around 0.00001.
numberIterations: The is the number of iterations that the
program executes before stopping and displaying all of the
graphic results.
predictionFilterLength: This is the number of coefficients
in the prediction filter. This can be any integer value
greater than zero. The program will throw an exception if
this value is zero. Typical values are 15 to 30. Longer
filters tend to produce better results in terms of the
narrowness of the notches at the noise frequencies and the
flatness of the filter between the notches.
signalScale: A scale factor that is applied to the wide
band signal provided by the random noise generator. The
random noise generator produces uniformly distributed
values ranging from -0.5 to +0.5. Scaling values of from 10
to 20 work well in terms of producing a wide-band signal
that is of a suitable magnitude for plotting. Set this to 0
to see how the program behaves in the presence of noise and
the absence of signal.
noiseScale: A scale factor that is applied to each of the
sinusoidal noise functions before they are added to the
signal. The raw sinusoids vary from -1.0 to +1.0. Scaling
values of from 10 to 20 work well in terms of being of a
suitable magnitude for plotting. Set this to 0 to see how
the program behaves in the presence of wide-band signal and
the absence of narrow-band noise.
numberNoiseSources: This value specifies the number of
sinusoidal noise components that are added to the wide-band
signal. Must be an integer value from 0 to 3.
Tested using J2SE 5.0 and WinXP. J2SE 5.0 or later is
required.
**********************************************************/
import static java.lang.Math.*;//J2SE 5.0 req
class Adapt02{
public static void main(String[] args){
//Default parameter values
double feedbackGain = 0.00001;
int numberIterations = 500;
int predictionFilterLength = 26;
double signalScale = 20;
double noiseScale = 20;
int numberNoiseSources = 1;
if(args.length != 6){
System.out.println(
"Usage with all parameters following " +
"program name:\n" +
"java Adapt02\n" +
"feedbackGain\n" +
"numberIterations\n" +
"predictionFilterLength\n" +
"signalScale\n" +
"noiseScale\n" +
"numberNoiseSources\n");
System.out.println(
"Using following values by default:\n" +
"feedbackGain: " + feedbackGain +
"\nnumberIterations: " + numberIterations +
"\npredictionFilterLength: " +
predictionFilterLength +
"\nsignalScale: " + signalScale +
"\nnoiseScale: " + noiseScale +
"\nnumberNoiseSources: " + numberNoiseSources);
}else{//Command line params were provided.
feedbackGain = Double.parseDouble(args[0]);
numberIterations = Integer.parseInt(args[1]);
predictionFilterLength = Integer.parseInt(args[2]);
signalScale = Double.parseDouble(args[3]);
noiseScale = Double.parseDouble(args[4]);
numberNoiseSources = Integer.parseInt(args[5]);
System.out.println(
"Using following values from input:\n" +
"feedbackGain: " + feedbackGain +
"\nnumberIterations: " + numberIterations +
"\npredictionFilterLength: " +
predictionFilterLength +
"\nsignalScale: " + signalScale +
"\nnoiseScale: " + noiseScale +
"\nnumberNoiseSources: " + numberNoiseSources);
}//end else
//Instantiate a new object of the Adapt02 class and
// invoke the method named process on that object.
new Adapt02().process(feedbackGain,
numberIterations,
predictionFilterLength,
signalScale,
noiseScale,
numberNoiseSources);
}//end main
//-----------------------------------------------------//
//This is the primary adaptive processing and plotting
// method for the program.
void process(double feedbackGain,
int numberIterations,
int predictionFilterLength,
double signalScale,
double noiseScale,
int numberNoiseSources){
//Create the initial predictionFilter containing all
// zero values. You could initialize this to different
// values if you wanted to.
double[] predictionFilter =
new double[predictionFilterLength];
//Create the initial whiteningFilter and initialize it
// for spectrum analysis and plotting by copying the
// initial prediction filter into the lower elements of
// the whitening filter.
double[] whiteningFilter =
new double[predictionFilter.length + 1];
System.arraycopy(predictionFilter,
0,
whiteningFilter,
0,
predictionFilter.length);
//Set the final value in the whitening filter to -1.
whiteningFilter[whiteningFilter.length - 1] = -1;
//Create an array to serve as a two-sample delay line
// for the raw data.
double[] rawData = new double[2];
//Create an array to serve as a processing delay line
// for the data being processed.
double[] chanA = new double[predictionFilter.length];
//Instantiate a plotting object for six channels of
// time-series data.
PlotALot07 timePlotObj =
new PlotALot07("Time",468,200,25,10,4,4);
//Instantiate a plotting object for two channels of
// filter frequency response data. One channel is for
// the amplitude and the other channel is the phase.
PlotALot03 freqPlotObj =
new PlotALot03("Freq",264,487,35,2,0,0);
//Instantiate a plotting object to display the
// whitening filter at specific time intervals during
// the adaptive process. Note that the minimum
// allowable width for a Java Frame object is 112
// pixels under WinXP. Therefore, the following
// display doesn't synchronize properly for prediction
// filter lengths less than 25 coefficients. However,
// the code that feeds data to the plotting object
// later in the program extends the length of the
// filter to cause it to synchronize and to plot one
// set of filter coefficients on each axis.
PlotALot01 filterPlotObj = new PlotALot01("Filter",
(whiteningFilter.length * 4) + 8,487,70,4,0,0);
//Declare and initialize working variables.
double output = 0;
double err = 0;
double target = 0;
double input = 0;
double signal = 0;
double sineNoise = 0;
//Display frequency response of initial whitening
// filter computed at 128 points between zero and the
// folding frequency.
displayFreqResponse(whiteningFilter,freqPlotObj,128,
whiteningFilter.length - 1);
//Display the initial whitening filter as a time series
// on the first axis.
for(int cnt = 0;cnt < whiteningFilter.length;cnt++){
filterPlotObj.feedData(40*whiteningFilter[cnt]);
}//end for loop
//Extend the whitening filter with a value of 2.5 for
// display purposes only if it is too short to
// synchronize properly with the plotting software.
// This value of 2.5 is easily recognizable in the
// plot as artificial extended data. See earlier
// comment on this topic.
//Note that this approach to forcing synchronization
// will not cause the plot to synchronize properly on
// an operating system for which the sum of the left
// and right insets on a Frame object are different
// from 8 pixels. The same approach to synchronization
// could be used but the minimum synchronizable filter
// length would probably be different.
if(whiteningFilter.length <= 26){
for(int cnt = 0;cnt < (26 - whiteningFilter.length);
cnt++){
filterPlotObj.feedData(2.5);
}//end for loop
}//end if
//Do the iterative adaptive process
for(int cnt = 0;cnt < numberIterations;cnt++){
//Get the next sample of wideband signal.
signal = signalScale*(Math.random() - 0.5);
//Get the next sample of sinusoidal noise containing
// three, two, or one sinusoid.
if(numberNoiseSources == 3){
sineNoise = noiseScale*(Math.sin(2*cnt*PI/8) +
Math.sin(2*cnt*PI/5) +
Math.sin(2*cnt*PI/3));
}else if(numberNoiseSources == 2){
sineNoise = noiseScale*(Math.sin(2*cnt*PI/8) +
Math.sin(2*cnt*PI/5));
}else if(numberNoiseSources == 1){
sineNoise = noiseScale*(Math.sin(2*cnt*PI/8));
}else{
System.out.println(
"Incorrect number noise sources, terminating");
System.exit(0);
}//end else
//Insert the signal plus noise into the raw data
// delay line.
flowLine(rawData,signal + sineNoise);
//Populate chanA with the next to the last value in
// the raw data delay line. The last sample value in
// the delay line will be the adaptive target.
flowLine(chanA,rawData[rawData.length - 2]);
//Get the most recent sample that was put into the
// chanA delay line and save for plotting.
input = chanA[chanA.length -1];
//Apply the current predictionFilter to the data
// contained in the chanA delay line.
output = dotProduct(predictionFilter,chanA);
//Get the signal plus noise sample from the end of
// the raw data delay line for an adaptive target.
target = rawData[rawData.length - 1];
//Compute the error between the current filter output
// and the target.
err = output - target;
//Use the error to update the predictionFilter
// coefficients.
for(int ctr = 0;ctr < predictionFilter.length;ctr++){
predictionFilter[ctr] -=
err*chanA[ctr]*feedbackGain;
}//end for loop. This is the end of the adaptive
// process. Code following this point in the program
// is used for display only.
//Feed the time series data to the plotting object.
timePlotObj.feedData(
-err,signal,sineNoise,input,output,target);
//Compute and plot the frequency response and plot
// the whitening filter every 100 iterations.
if(cnt%100 == 0){
//Create a whitening filter from the data in the
// prediction filter. Begin by copying the
// prediction filter into the bottom elements of
// the whitening filter.
System.arraycopy(predictionFilter,
0,
whiteningFilter,
0,
predictionFilter.length);
//Now set the final value in the whitening filter
// to -1. A whitening filter is a prediction filter
// with a -1 appended to its end.
whiteningFilter[whiteningFilter.length - 1] = -1;
displayFreqResponse(whiteningFilter,freqPlotObj,
128,whiteningFilter.length - 1);
//Display the whitening filter coefficient values.
for(int ctr = 0;ctr < whiteningFilter.length;
ctr++){
filterPlotObj.feedData(40*whiteningFilter[ctr]);
}//end for loop
//Extend the whitening filter with a value of 2.5
// for plotting if necessary to cause it to
// synchronize with one filter on each axis.
// See explanatory comment earlier.
if(whiteningFilter.length <= 26){
for(int count = 0;
count < (26-whiteningFilter.length);count++){
filterPlotObj.feedData(2.5);
}//End for loop
}//End if statement
}//End display of frequency response and whitening
// filter
}//End for loop, End adaptive process
//Cause all the data to be plotted.
timePlotObj.plotData();
freqPlotObj.plotData(0,201);
filterPlotObj.plotData(265,201);
}//end process method
//-----------------------------------------------------//
//This method simulates a tapped delay line. It receives
// a reference to an array and a value. It discards the
// value at index 0 of the array, moves all the other
// values by one element toward 0, and inserts the new
// value at the top of the array.
void flowLine(double[] line,double val){
for(int cnt = 0;cnt < (line.length - 1);cnt++){
line[cnt] = line[cnt+1];
}//end for loop
line[line.length - 1] = val;
}//end flowLine
//-----------------------------------------------------//
//This method receives two arrays and treats the first n
// elements in each of the two arrays as a pair of
// vectors. It computes and returns the vector dot
// product of the two vectors. If the length of one
// array is greater than the length of the other array,
// it considers the number of dimensions of the vectors
// to be equal to the length of the smaller array.
double dotProduct(double[] v1,double[] v2){
double result = 0;
if((v1.length) <= (v2.length)){
for(int cnt = 0;cnt < v1.length;cnt++){
result += v1[cnt]*v2[cnt];
}//end for loop
return result;
}else{
for(int cnt = 0;cnt < v2.length;cnt++){
result += v1[cnt]*v2[cnt];
}//med for loop
return result;
}//end else
}//end dotProduct
//-----------------------------------------------------//
void displayFreqResponse(
double[] filter,PlotALot03 plot,int len,int zeroTime){
//Create the arrays required by the Fourier Transform.
double[] timeDataIn = new double[len];
double[] realSpect = new double[len];
double[] imagSpect = new double[len];
double[] angle = new double[len];
double[] magnitude = new double[len];
//Copy the filter into the timeDataIn array
System.arraycopy(filter,0,timeDataIn,0,filter.length);
//Compute DFT of the filter from zero to the folding
// frequency and save it in the output arrays.
ForwardRealToComplex01.transform(timeDataIn,
realSpect,
imagSpect,
angle,
magnitude,
zeroTime,
0.0,
0.5);
//Display the magnitude data. Convert to normalized
// decibels first.
//Eliminate or change any values that are incompatible
// with log10 method.
for(int cnt = 0;cnt < magnitude.length;cnt++){
if((magnitude[cnt] == Double.NaN) ||
(magnitude[cnt] <= 0)){
//Replace the magnitude by a very small positive
// value.
magnitude[cnt] = 0.0000001;
}else if(magnitude[cnt] == Double.POSITIVE_INFINITY){
//Replace the magnitude by a very large positive
// value.
magnitude[cnt] = 9999999999.0;
}//end else if
}//end for loop
//Now convert magnitude data to log base 10
for(int cnt = 0;cnt < magnitude.length;cnt++){
magnitude[cnt] = log10(magnitude[cnt]);
}//end for loop
//Note that from this point forward, all references to
// magnitude are referring to log base 10 data, which
// can be thought of as scaled decibels.
//Find the absolute peak value. Begin with a negative
// peak value with a large magnitude and replace it
// with the largest magnitude value.
double peak = -9999999999.0;
for(int cnt = 0;cnt < magnitude.length;cnt++){
if(peak < abs(magnitude[cnt])){
peak = abs(magnitude[cnt]);
}//end if
}//end for loop
//Normalize to 50 times the peak value and shift up the
// page by 50 units to make the values compatible with
// the plotting program. Recall that adding a
// constant to log values is equivalent to scaling the
// original data.
for(int cnt = 0;cnt < magnitude.length;cnt++){
magnitude[cnt] = 50*magnitude[cnt]/peak + 50;
}//end for loop
//Now feed the normalized decibel data to the plotting
// system.
for(int cnt = 0;cnt < magnitude.length;cnt++){
plot.feedData(magnitude[cnt],angle[cnt]/20);
}//end for loop
}//end displayFreqResponse
//-----------------------------------------------------//
}//end class Adapt02
|
/*File PlotALot07.java
Copyright 2005, R.G.Baldwin
This program is an update to the program named
PlotALot04 for the purpose of plotting six
data channels. See PlotALot04 for descriptive
comments. Otherwise, the comments in this
program have not been updated to reflect this
update.
The program was tested using J2SE 5.0 and WinXP.
Requires J2SE 5.0 to support generics.
************************************************/
import java.awt.*;
import java.awt.event.*;
import java.util.*;
public class PlotALot07{
//This main method is provided so that the
// class can be run as an application to test
// itself.
public static void main(String[] args){
//Instantiate a plotting object using the
// version of the constructor that allows for
// controlling the plotting parameters.
PlotALot07 plotObjectA =
new PlotALot07("A",158,350,25,5,4,4);
//Feed quadruplets of data values to the
// plotting object.
for(int cnt = 0;cnt < 115;cnt++){
//Plot some white random noise. Note that
// fifteen of the values for each time
// series are not random. See the opening
// comments for a discussion of the reasons
// why.
double valBlack = (Math.random() - 0.5)*25;
double valRed = valBlack;
double valBlue = valBlack;
double valGreen = valBlack;
double valMagenta = valBlack;
double valCyan = valBlack;
//Feed quadruplets of values to the plotting
// object by invoking the feedData method
// once for each quadruplet of data values.
if(cnt == 57){
plotObjectA.feedData(0,0,0,0,0,0);
}else if(cnt == 58){
plotObjectA.feedData(0,0,0,0,0,0);
}else if(cnt == 59){
plotObjectA.feedData(25,25,25,25,25,25);
}else if(cnt == 60){
plotObjectA.feedData(-25,-25,-25,-25,-25,-25);
}else if(cnt == 61){
plotObjectA.feedData(25,25,25,25,25,25);
}else if(cnt == 62){
plotObjectA.feedData(0,0,0,0,0,0);
}else if(cnt == 63){
plotObjectA.feedData(0,0,0,0,0,0);
}else if(cnt == 26){
plotObjectA.feedData(0,0,0,0,0,0);
}else if(cnt == 27){
plotObjectA.feedData(0,0,0,0,0,0);
}else if(cnt == 28){
plotObjectA.feedData(20,20,20,20,20,20);
}else if(cnt == 29){
plotObjectA.feedData(20,20,20,20,20,20);
}else if(cnt == 30){
plotObjectA.feedData(-20,-20,-20,-20,-20,-20);
}else if(cnt == 31){
plotObjectA.feedData(-20,-20,-20,-20,-20,-20);
}else if(cnt == 32){
plotObjectA.feedData(0,0,0,0,0,0);
}else if(cnt == 33){
plotObjectA.feedData(0,0,0,0,0,0);
}else{
plotObjectA.feedData(valBlack,
valRed,
valBlue,
valGreen,
valMagenta,
valCyan);
}//end else
}//end for loop
//Cause the data to be plotted in the default
// screen location.
plotObjectA.plotData();
}//end main
//-------------------------------------------//
String title;
int frameWidth;
int frameHeight;
int traceSpacing;//pixels between traces
int sampSpacing;//pixels between samples
int ovalWidth;//width of sample marking oval
int ovalHeight;//height of sample marking oval
int tracesPerPage;
int samplesPerPage;
int pageCounter = 0;
int sampleCounter = 0;
ArrayList <Page> pageLinks =
new ArrayList<Page>();
//There are two overloaded versions of the
// constructor for this class. This
// overloaded version accepts several incoming
// parameters allowing the user to control
// various aspects of the plotting format. A
// different overloaded version accepts a title
// string only and sets all of the plotting
// parameters to default values.
PlotALot07(String title,//Frame title
int frameWidth,//in pixels
int frameHeight,//in pixels
int traceSpacing,//in pixels
int sampSpace,//in pixels per sample
int ovalWidth,//sample marker width
int ovalHeight)//sample marker hite
{//constructor
//Specify sampSpace as pixels per sample.
// Should never be less than 1. Convert to
// pixels between samples for purposes of
// computation.
this.title = title;
this.frameWidth = frameWidth;
this.frameHeight = frameHeight;
this.traceSpacing = traceSpacing;
//Convert to pixels between samples.
this.sampSpacing = sampSpace - 1;
this.ovalWidth = ovalWidth;
this.ovalHeight = ovalHeight;
//The following object is instantiated solely
// to provide information about the width and
// height of the canvas. This information is
// used to compute a variety of other
// important values.
Page tempPage = new Page(title);
int canvasWidth = tempPage.canvas.getWidth();
int canvasHeight =
tempPage.canvas.getHeight();
//Display information about this plotting
// object.
System.out.println("\nTitle: " + title);
System.out.println(
"Frame width: " + tempPage.getWidth());
System.out.println(
"Frame height: " + tempPage.getHeight());
System.out.println(
"Page width: " + canvasWidth);
System.out.println(
"Page height: " + canvasHeight);
System.out.println(
"Trace spacing: " + traceSpacing);
System.out.println(
"Sample spacing: " + (sampSpacing + 1));
if(sampSpacing < 0){
System.out.println("Terminating");
System.exit(0);
}//end if
//Get rid of this temporary page.
tempPage.dispose();
//Now compute the remaining important values.
tracesPerPage =
(canvasHeight - traceSpacing/2)/
traceSpacing;
System.out.println("Traces per page: "
+ tracesPerPage);
if((tracesPerPage == 0) ||
(tracesPerPage%6 != 0) ){
System.out.println("Terminating program");
System.exit(0);
}//end if
samplesPerPage = canvasWidth * tracesPerPage/
(sampSpacing + 1)/6;
System.out.println("Samples per page: "
+ samplesPerPage);
//Now instantiate the first usable Page
// object and store its reference in the
// list.
pageLinks.add(new Page(title));
}//end constructor
//-------------------------------------------//
PlotALot07(String title){
//Invoke the other overloaded constructor
// passing default values for all but the
// title.
this(title,400,410,50,2,2,2);
}//end overloaded constructor
//-------------------------------------------//
//Invoke this method once for each quadruplet of
// data values to be plotted.
void feedData(double valBlack,
double valRed,
double valBlue,
double valGreen,
double valMagenta,
double valCyan){
if((sampleCounter) == samplesPerPage){
//if the page is full, increment the page
// counter, create a new empty page, and
// reset the sample counter.
pageCounter++;
sampleCounter = 0;
pageLinks.add(new Page(title));
}//end if
//Store the sample values in the MyCanvas
// object to be used later to paint the
// screen. Then increment the sample
// counter. The sample values pass through
// the page object into the current MyCanvas
// object.
pageLinks.get(pageCounter).putData(
valBlack,
valRed,
valBlue,
valGreen,
valMagenta,
valCyan,
sampleCounter);
sampleCounter++;
}//end feedData
//-------------------------------------------//
//There are two overloaded versions of the
// plotData method. One version allows the
// user to specify the location on the screen
// where the stack of plotted pages will
// appear. The other version places the stack
// in the upper left corner of the screen.
//Invoke one of the overloaded versions of
// this method once when all data has been fed
// to the plotting object in order to rearrange
// the order of the pages with page 0 at the
// top of the stack on the screen.
//For this overloaded version, specify xCoor
// and yCoor to control the location of the
// stack on the screen. Values of 0,0 will
// place the stack at the upper left corner of
// the screen. Also see the other overloaded
// version, which places the stack at the upper
// left corner of the screen by default.
void plotData(int xCoor,int yCoor){
Page lastPage =
pageLinks.get(pageLinks.size() - 1);
//Delay until last page becomes visible.
while(!lastPage.isVisible()){
//Loop until last page becomes visible
}//end while loop
Page tempPage = null;
//Make all pages invisible
for(int cnt = 0;cnt < (pageLinks.size());
cnt++){
tempPage = pageLinks.get(cnt);
tempPage.setVisible(false);
}//end for loop
//Now make all pages visible in reverse order
// so that page 0 will be on top of the
// stack on the screen.
for(int cnt = pageLinks.size() - 1;cnt >= 0;
cnt--){
tempPage = pageLinks.get(cnt);
tempPage.setLocation(xCoor,yCoor);
tempPage.setVisible(true);
}//end for loop
}//end plotData(int xCoor,int yCoor)
//-------------------------------------------//
//This overloaded version of the method causes
// the stack to be located in the upper left
// corner of the screen by default
void plotData(){
plotData(0,0);//invoke overloaded version
}//end plotData()
//-------------------------------------------//
//Inner class. A PlotALot07 object may
// have as many Page objects as are required
// to plot all of the data values. The
// reference to each Page object is stored
// in an ArrayList object belonging to the
// PlotALot07 object.
class Page extends Frame{
MyCanvas canvas;
int sampleCounter;
Page(String title){//constructor
canvas = new MyCanvas();
add(canvas);
setSize(frameWidth,frameHeight);
setTitle(title + " Page: " + pageCounter);
setVisible(true);
//---------------------------------------//
//Anonymous inner class to terminate the
// program when the user clicks the close
// button on the Frame.
addWindowListener(
new WindowAdapter(){
public void windowClosing(
WindowEvent e){
System.exit(0);//terminate program
}//end windowClosing()
}//end WindowAdapter
);//end addWindowListener
//---------------------------------------//
}//end constructor
//=========================================//
//This method receives a quadruplet of sample
// values of type double and stores each of
// them in a separate array object belonging
// to the MyCanvas object.
void putData(double valBlack,
double valRed,
double valBlue,
double valGreen,
double valMagenta,
double valCyan,
int sampleCounter){
canvas.blackData[sampleCounter] = valBlack;
canvas.redData[sampleCounter] = valRed;
canvas.blueData[sampleCounter] = valBlue;
canvas.greenData[sampleCounter] = valGreen;
canvas.magentaData[sampleCounter] = valMagenta;
canvas.cyanData[sampleCounter] = valCyan;
//Save the sample counter in an instance
// variable to make it available to the
// overridden paint method. This value is
// needed by the paint method so it will
// know how many samples to plot on the
// final page which probably won't be full.
this.sampleCounter = sampleCounter;
}//end putData
//=========================================//
//Inner class
class MyCanvas extends Canvas{
double [] blackData =
new double[samplesPerPage];
double [] redData =
new double[samplesPerPage];
double [] blueData =
new double[samplesPerPage];
double [] greenData =
new double[samplesPerPage];
double [] magentaData =
new double[samplesPerPage];
double [] cyanData =
new double[samplesPerPage];
//Override the paint method
public void paint(Graphics g){
//Draw horizontal axes, one for each
// trace.
for(int cnt = 0;cnt < tracesPerPage;
cnt++){
g.drawLine(0,
(cnt+1)*traceSpacing,
this.getWidth(),
(cnt+1)*traceSpacing);
}//end for loop
//Plot the points if there are any to be
// plotted.
if(sampleCounter > 0){
for(int cnt = 0;cnt <= sampleCounter;
cnt++){
//Begin by plotting the values from
// the blackData array object.
g.setColor(Color.BLACK);
//Compute a vertical offset to locate
// the black data on every third axis
// on the page.
int yOffset =
((1 + cnt*(sampSpacing + 1)/
this.getWidth())*6*traceSpacing)
- 5*traceSpacing;
//Draw an oval centered on the sample
// value to mark the sample in the
// plot. It is best if the dimensions
// of the oval are evenly divisable
// by 2 for centering purposes.
//Reverse the sign of the sample
// value to cause positive sample
// values to be plotted above the
// axis.
g.drawOval(cnt*(sampSpacing + 1)%
this.getWidth() - ovalWidth/2,
yOffset - (int)blackData[cnt]
- ovalHeight/2,
ovalWidth,
ovalHeight);
//Connect the sample values with
// straight lines. Do not draw a
// line connecting the last sample in
// one trace to the first sample in
// the next trace.
if(cnt*(sampSpacing + 1)%
this.getWidth() >=
sampSpacing + 1){
g.drawLine(
(cnt - 1)*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)blackData[cnt-1],
cnt*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)blackData[cnt]);
}//end if
//Now plot the data stored in the
// redData array object.
g.setColor(Color.RED);
//Compute a vertical offset to locate
// the red data on every third axis
// on the page.
yOffset = (1 + cnt*(sampSpacing + 1)/
this.getWidth())*6*traceSpacing
- 4*traceSpacing;
//Draw the ovals as described above.
g.drawOval(cnt*(sampSpacing + 1)%
this.getWidth() - ovalWidth/2,
yOffset - (int)redData[cnt]
- ovalHeight/2,
ovalWidth,
ovalHeight);
//Connect the sample values with
// straight lines as described above.
if(cnt*(sampSpacing + 1)%
this.getWidth() >=
sampSpacing + 1){
g.drawLine(
(cnt - 1)*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)redData[cnt-1],
cnt*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)redData[cnt]);
}//end if
//Now plot the data stored in the
// blueData array object.
g.setColor(Color.BLUE);
//Compute a vertical offset to locate
// the blue data on every third axis
// on the page.
yOffset = (1 + cnt*(sampSpacing + 1)/
this.getWidth())*6*traceSpacing
-3*traceSpacing;
//Draw the ovals as described above.
g.drawOval(cnt*(sampSpacing + 1)%
this.getWidth() - ovalWidth/2,
yOffset - (int)blueData[cnt]
- ovalHeight/2,
ovalWidth,
ovalHeight);
//Connect the sample values with
// straight lines as described above.
if(cnt*(sampSpacing + 1)%
this.getWidth() >=
sampSpacing + 1){
g.drawLine(
(cnt - 1)*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)blueData[cnt-1],
cnt*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)blueData[cnt]);
}//end if
//Now plot the data stored in the
// greenData array object.
g.setColor(Color.GREEN);
//Compute a vertical offset to locate
// the green data on every third axis
// on the page.
yOffset = (1 + cnt*(sampSpacing + 1)/
this.getWidth())*6*traceSpacing
-2*traceSpacing;
//Draw the ovals as described above.
g.drawOval(cnt*(sampSpacing + 1)%
this.getWidth() - ovalWidth/2,
yOffset - (int)greenData[cnt]
- ovalHeight/2,
ovalWidth,
ovalHeight);
//Connect the sample values with
// straight lines as described above.
if(cnt*(sampSpacing + 1)%
this.getWidth() >=
sampSpacing + 1){
g.drawLine(
(cnt - 1)*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)greenData[cnt-1],
cnt*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)greenData[cnt]);
}//end if
//Now plot the data stored in the
// magentaData array object.
g.setColor(Color.MAGENTA);
//Compute a vertical offset to locate
// the magenta data on every third axis
// on the page.
yOffset = (1 + cnt*(sampSpacing + 1)/
this.getWidth())*6*traceSpacing
-traceSpacing;
//Draw the ovals as described above.
g.drawOval(cnt*(sampSpacing + 1)%
this.getWidth() - ovalWidth/2,
yOffset - (int)magentaData[cnt]
- ovalHeight/2,
ovalWidth,
ovalHeight);
//Connect the sample values with
// straight lines as described above.
if(cnt*(sampSpacing + 1)%
this.getWidth() >=
sampSpacing + 1){
g.drawLine(
(cnt - 1)*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)magentaData[cnt-1],
cnt*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)magentaData[cnt]);
}//end if
//Now plot the data stored in the
// cyanData array object.
g.setColor(Color.CYAN);
//Compute a vertical offset to locate
// the cyan data on every third axis
// on the page.
yOffset = (1 + cnt*(sampSpacing + 1)/
this.getWidth())*6*traceSpacing;
//Draw the ovals as described above.
g.drawOval(cnt*(sampSpacing + 1)%
this.getWidth() - ovalWidth/2,
yOffset - (int)cyanData[cnt]
- ovalHeight/2,
ovalWidth,
ovalHeight);
//Connect the sample values with
// straight lines as described above.
if(cnt*(sampSpacing + 1)%
this.getWidth() >=
sampSpacing + 1){
g.drawLine(
(cnt - 1)*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)cyanData[cnt-1],
cnt*(sampSpacing + 1)%
this.getWidth(),
yOffset - (int)cyanData[cnt]);
}//end if
}//end for loop
}//end if for sampleCounter > 0
}//end overridden paint method
}//end inner class MyCanvas
}//end inner class Page
}//end class PlotALot07
//=============================================//
|
Copyright 2005, Richard G. Baldwin. Reproduction in whole or in part in any form or medium without express written permission from Richard Baldwin is prohibited.
Richard has participated in numerous consulting projects and he frequently provides onsite training at the high-tech companies located in and around Austin, Texas. He is the author of Baldwin's Programming Tutorials, which have gained a worldwide following among experienced and aspiring programmers. He has also published articles in JavaPro magazine.
In addition to his programming expertise, Richard has many years of practical experience in Digital Signal Processing (DSP). His first job after he earned his Bachelor's degree was doing DSP in the Seismic Research Department of Texas Instruments. (TI is still a world leader in DSP.) In the following years, he applied his programming and DSP expertise to other interesting areas including sonar and underwater acoustics.
Richard holds an MSEE degree from Southern Methodist University and has many years of experience in the application of computer technology to real-world problems.
Keywords
Java adaptive filtering convolution filter frequency spectrum LMS amplitude
phase time-delay linear DSP impulse decibel log10 DFT transform bandwidth signal
noise real-time dot-product vector time-series prediction whitening
-end-