Published: October 23, 2007
By Richard G. Baldwin
Java Programming Notes # 1544
Third in a series of lessons
This is the third lesson in a series of lessons designed to start with Java 3D basics and work up to the general complexity of the program that I explained in the earlier lesson titled "Understanding Lighting in the Java 3D API" (see Resources).
The first lesson in this series was titled "Back to Basics in the Java 3D API" (see Resources). The previous lesson was titled "Digging a Little Deeper into the Java 3D API." This lesson is titled "Simple Animation with the Java 3D API." My current plan is for future lessons to deal with the detailed behavior of an Alpha time-base object, user and object interaction as well as advanced animation and textures.
What you will learn
In this lesson, I will teach you how to use the RotationInterpolator and Alpha classes of the Java 3D API, along with other necessary classes, to write a simple animation program. I will also explain the rationale by which those classes are used to write animation programs.
Compiling and running Java 3D programs
In order to compile and run programs using the Java 3D API, you will need to download and install the Java 3D API software. As of the date of this writing, version 1.5.0 is available for download.
In addition, you will need to download and install either Microsoft DirectX or OpenGL. All of the sample programs in this series of tutorials were developed and tested using Microsoft DirectX. They were not tested using OpenGL.
Much of what I will be teaching you about the use of the Java 3D API was learned by studying the tutorial by Dennis J Bouvier (see Resources) along with other online material, some of which is also listed in Resources.
You can view the Bouvier tutorial online. You can also download the Bouvier tutorial as a set of PDF files along with the source code for the example programs in his tutorial.
I recommend that you open another copy of this document in a separate browser window and use the following links to easily find and view the figures and listings while you are reading about them.
I recommend that you also study the other lessons in my extensive collection of online Java tutorials. You will find a consolidated index at www.DickBaldwin.com.
The need to understand animation
It seems that one of the first things that programming students want to do these days is to write game programs. Modern game programs almost always involve animation. Therefore, before a student can write a game program, that student must understand animation (in addition to many other important programming concepts).
|
Animation versus interactive behavior
In reality, most modern game programs involve both animation and interaction (see the sidebar). This lesson will deal with animation. Interactive behavior using the Java 3D API will be reserved for a future lesson.
Simple versus advanced animation
Animation can involve some very complex programming concepts. Fortunately, simple animation is relatively easy to achieve using the Java 3D API once you understand the required structure. This lesson will concentrate on simple animation for the purpose of exposing the underlying capabilities of Java 3D in this regard. Advanced animation behavior will be reserved for a future lesson.
Bouvier's recipe for animation in Java 3D
Although it's not the only way to create animation, one way to create animation in Java 3D is through the use an Interpolator object. (That is the approach that will be used in this lesson.) Bouvier's recipe for using an Interpolator to create animation consists of the five steps shown in Figure 1.
Figure 1. Bouvier's recipe for animation in Java 3D.
|
Most of the terminology in Figure 1 will probably mean very little to you at this point. However, by the end of this lesson, you should be able to understand the meaning of each of the steps in Figure 1. When you have finished studying this lesson, you should understand the rudiments of creating Java 3D programs that exhibit animation behavior.
In this lesson, I will present and explain a program named Java3D005. The purpose of this program is to create a simple animation that will animate the virtual universe that was developed in the previous lesson in the program named Java3D004.
Four screen shots
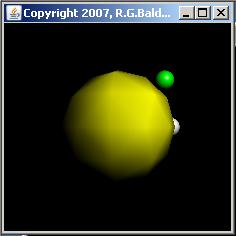
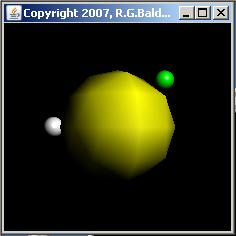
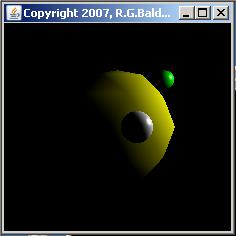
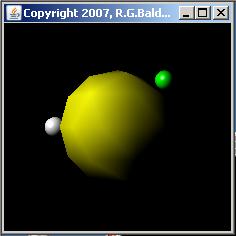
Figure 2 shows four screen shots that were taken while the program was running. The top two images were taken while one version of the program was running. The bottom two images were taken while a different version of the program was running.
Figure 2. Four screen shots from the running animation program.
 |
 |
 |
 |
A screen shot from the original program
Figure 3 shows a screen shot from the original version of the program named Java3D004. This is the virtual universe that was modified slightly and animated in this new program.
Figure 3. A screen shot from the original program.
|
|
The location of the white sphere was changed
You will note in Figure 3 that the white sphere is down, to the left of, and in front of the yellow sphere. The location of the white sphere was changed in the animated version of the universe in this program. The change causes the white sphere to be in the horizontal plane defined by the X and Z axes. This makes it relatively easy to animate the white sphere so as to make it appear to be in a synchronous circular orbit around the yellow sphere.
Figure 4 shows the beginning (and ending) location for the white sphere in this animation program. (Compare Figure 4 with Figure 3 to see the difference.)
Figure 4. New location for the white sphere.
|
|
Two versions of the program
Two different versions of this version are presented and explained in this lesson. In the primary version, the universe was animated by causing the yellow sphere to slowly rotate on its vertical axis through one complete revolution. The yellow sphere carries the small white sphere along with it just as though the white sphere is orbiting the yellow sphere in a synchronous circular orbit. The small green sphere does not rotate with the yellow sphere, but maintains its original position. The point light source also maintains its original position.
Screen shots from the first version
The top two images in Figure 2 show two screen shots taken from this version of the program while it was running. The image on the top left shows the universe just before the white sphere disappeared behind the yellow sphere, moving from right to left behind the yellow sphere. The image on the top right shows the universe just as the white sphere was emerging from behind the yellow sphere on the left.
Facets or divisions on the yellow sphere
I purposely used a small value for the number of divisions (facets) for the yellow sphere to cause it to have an uneven surface. This makes it possible to see that the yellow sphere is actually rotating around its vertical axis by observing the movement of the highlights emitted by the facets on the surface of the yellow sphere. Otherwise, the fact that the yellow sphere is rotating would not be visible because the surface of the sphere would be the same all over, containing no identifying features.
|
The second version
The second version of the program (see the sidebar) causes the light source to also rotate around the vertical axis in 3D space in synchronism with the rotation of the yellow sphere. This produces a very different animation effect, which causes shadows to move across surfaces of the spheres.
The original position of the light source
The bottom two images in Figure 2 show screen shots from this version of the program while it is running. The original (and final) position of the light source is above the center of, to the right of, and in front of the yellow sphere (sort of over the viewer's right shoulder). This location is indicated by the illumination of the yellow sphere in the top two images in Figure 2.
Two screen shots from the running program
The bottom left image in Figure 2 shows the point in time where the white sphere and the light source were moving around the right side of the yellow sphere (moving from front to back at this point). Thus, the right sides of all three spheres are illuminated. The light source leads the white sphere by about 30 degrees, causing only a small portion of the white sphere to be illuminated (from the viewpoint of the viewer) in this image.
The bottom right image shows the point in time where the white sphere and the light source were just emerging from behind the yellow sphere on it's left side (moving from back to front at this point), causing the left side of all three spheres to be illuminated.
Testing
This program was tested using Java SE 6, and Java 3D 1.5.0 running under Windows XP.
Much of the code in this program is very similar to, or identical to code that I presented and explained in the previous lesson titled "Digging a Little Deeper into the Java 3D API" (see Resources). Therefore, I won't repeat those explanations. Rather, I will simply make note of the fact that the code is similar to code explained in earlier lessons.
I will present and explain this program in fragments. A complete listing of the program is presented in Listing 12 near the end of the lesson. The first code fragment is shown in Listing 1.
Listing 1. The beginning of the program named Java3D005.
//This is the top-level driver class for this program.
// This program could be written without the use of this
// driver class. However, I decided to keep it intact
// for future expansions that require a user input GUI.
public class Java3D005 extends Frame{
public static void main(String[] args){
Java3D005 thisObj = new Java3D005();
}//end main
//----------------------------------------------------//
public Java3D005(){//constructor
setTitle("Copyright 2007, R.G.Baldwin");
add(new Label("You can build a GUI here."));
setBounds(236,0,235,75);
setVisible(true);
//Instantiate the object in which the Java 3D
// universe will be displayed.
TheScene theScene = new TheScene();
//This window listener is used to terminate the
// program when the user clicks the X button.
addWindowListener(
new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}//end windowClosing
}//end new WindowAdapter
);//end addWindowListener
}//end constructor
//----------------------------------------------------//
//This is an inner class, from which the object in which
// the Java 3D universe will be displayed is
// instantiated.
class TheScene extends Frame{
TheScene(){//constructor
//Create a Canvas3D object to be used for rendering
// the Java 3D universe. Place it in the CENTER of
// the Frame.
Canvas3D canvas3D = new Canvas3D(
SimpleUniverse.getPreferredConfiguration());
add(BorderLayout.CENTER,canvas3D);
//Construct the objects that will be displayed in
// the scene
//Create and set properties for the large yellow
// sphere.
//Begin by describing the appearance of the surface
// of the large sphere. Make the color of the large
// sphere yellow.
Material yellowSphMaterial = new Material();
yellowSphMaterial.setDiffuseColor(1.0f,1.0f,0.0f);
Appearance yellowSphAppearance = new Appearance();
yellowSphAppearance.setMaterial(yellowSphMaterial);
//Now instantiate the large yellow sphere with 9
// divisions. Set the radius to 0.5. The reason for
// setting GENERATE_NORMALS is unclear at this time.
Sphere yellowSph = new Sphere(
0.5f,
Primitive.GENERATE_NORMALS,
9,
yellowSphAppearance);
|
With the exception of the need for some additional import directives, this program begins exactly like the program in the previous lesson. You can view the complete list of import directives in Listing 12
Create the small white sphere in a different location
The code in Listing 2 creates the small white sphere, but places it in a different location (as explained earlier) than was the case in the original program. The coordinate value that produced the change in location is highlighted in boldface in Listing 2.
Listing 2. Create the small white sphere in a different location.
//Now create a small white sphere with 50 divisions.
Material whiteSphMaterial = new Material();
whiteSphMaterial.setDiffuseColor(1.0f,1.0f,1.0f);
Appearance whiteSphAppearance = new Appearance();
whiteSphAppearance.setMaterial(whiteSphMaterial);
Sphere whiteSph = new Sphere(
0.10f,
Primitive.GENERATE_NORMALS,
50,
whiteSphAppearance);
//Translate the location of the white sphere to make
// it closer to the viewer than the yellow sphere at
// the origin.
Transform3D whiteTransform = new Transform3D();
//The following is a modification to the original
// virtual universe that causes the white sphere to
// be in the horizontal plane. This causes the
// white sphere to later be animated so as to appear
// to be in a synchronous orbit around the yellow
// sphere.
whiteTransform.setTranslation(
new Vector3f(-0.5f,-0.0f,0.5f));
TransformGroup whiteTransformGroup =
new TransformGroup();
whiteTransformGroup.setTransform(whiteTransform);
whiteTransformGroup.addChild(whiteSph);
|
More code with no changes
The code is Listing 3 is the same as the code in the original program.
Listing 3. More code with no changes.
//Now create a small green sphere located up to the
// right and behind the yellow sphere.
Material greenSphMaterial = new Material();
greenSphMaterial.setDiffuseColor(0.0f,1.0f,0.0f);
Appearance greenSphAppearance = new Appearance();
greenSphAppearance.setMaterial(greenSphMaterial);
Sphere greenSph = new Sphere(
0.10f,
Primitive.GENERATE_NORMALS,
50,
greenSphAppearance);
Transform3D greenTransform = new Transform3D();
greenTransform.setTranslation(
new Vector3f(0.5f,0.5f,-0.5f));
TransformGroup greenTransformGroup =
new TransformGroup();
greenTransformGroup.setTransform(greenTransform);
greenTransformGroup.addChild(greenSph);
//Add a white point light, in front of, to the
// right of, and above the yellow sphere.
Color3f pointLightColor =
new Color3f(1.0f,1.0f,1.0f);
Point3f pointLightPosition =
new Point3f(1.0f,1.0f,2.0f);
Point3f pointLightAttenuation =
new Point3f(1.0f,0.0f,0.0f);
PointLight pointLight = new PointLight(
pointLightColor,
pointLightPosition,
pointLightAttenuation);
|
Code with an expanded purpose
The code in Listing 4 is the same as corresponding code in the earlier program. However, the purpose of this code has been expanded. In particular, in this program, the BoundingSphere object is not only used to determine which objects to illuminate, it is also used to determine which objects to animate.
Listing 4. Code with an expanded purpose.
//Create a BoundingSphere object and use it to
// determine which objects to light. Also use it
// later to determine which objects to animate.
BoundingSphere boundingSphere =
new BoundingSphere(new Point3d(0.0,0.0,0.0),1.0);
pointLight.setInfluencingBounds(boundingSphere);
|
Some modified code
Listing 5 shows some code that was modified by deleting statements from the original code. The explanation for this change is highlighted in boldface comments in Listing 5.
Listing 5. Some modified code.
//Create an empty Java 3D universe and associate it
// with the Canvas3D object in the CENTER of the
// frame.
SimpleUniverse simpleUniverse =
new SimpleUniverse(canvas3D);
//Create and populate a BranchGroup object.
BranchGroup branchGroup = new BranchGroup();
//Add objects to the branchGroup. Note that the
// yellow and white spheres are no longer added to
// the branchGroup object, but rather are later
// added to a group that causes them to be animated.
branchGroup.addChild(greenTransformGroup);
//If you disable the following statement and enable
// a statement later that adds the pointLight to
// the rotationXform, you will see a very different
// effect. This will cause the light source to
// rotate with the yellow sphere causing the shadows
// to move across the spheres.
branchGroup.addChild(pointLight);
|
Beginning of the code that implements the animation
Listing 6 contains two new statements that begin the implementation of the animation. These two statements accomplish the first step in Bouvier's recipe in Figure 1.
Listing 6. Beginning of the code that implements the animation.
//THE CODE THAT IMPLEMENTS THE ANIMATION BEGINS HERE
TransformGroup rotationXform = new TransformGroup();
rotationXform.setCapability(
TransformGroup.ALLOW_TRANSFORM_WRITE);
|
Listing 6 creates a transform group that will be populated with the yellow sphere and the white sphere transform group. All objects or groups of objects belonging to this new group will be animated by subsequent code.
Setting the ALLOW_TRANSFORM_WRITE capability
As I understand it, by default, once an object or a group of objects is placed in a transform group, those objects cannot be accessed for modification. (Actually, it may be more correct to say that the behavior of the transform cannot be modified.) However, there are a number of capabilities that can be set on a transform group by calling the setCapability method on the group object. Listing 6 sets the ALLOW_TRANSFORM_WRITE capability on the new transform making it possible to modify the behavior of the transform over time in order to produce the animated behavior.
Create an Alpha object
Listing 7 creates an Alpha object that will be used to cause the objects in the rotationXform group (see Listing 6) to complete one animation cycle in 20 seconds (20,000 milliseconds). This satisfies step 2 in Bouvier's recipe shown in Figure 1.
Listing 7. Create an Alpha object.
Alpha rotationAlpha = new Alpha(1,20000); |
According to Sun,
"The alpha NodeComponent object provides common methods for converting a time value into an alpha value (a value in the range 0 to 1). The Alpha object is effectively a function of time that generates alpha values in the range [0,1] when sampled: f(t) = [0,1]. A primary use of the Alpha object is to provide alpha values for Interpolator behaviors. The function f(t) and the characteristics of the Alpha object are determined by user-definable parameters"
Stated more simply, an Alpha object provides a time base that can be used by an Interpolator object in the process of producing the intermediate views of the universe that are needed during an animation of the universe.
Four overloaded constructors
There are four different overloaded constructors for the Alpha class, with the most complex constructor requiring the following ten parameters:
A simpler constructor was used
Listing 7 uses a simpler constructor than that indicated above. According to Sun, the constructor used in Listing 7 "takes only the loopCount and increasingAlphaDuration as parameters and assigns the default values to all of the other parameters."
The first parameter in Listing 7 specifies that the animation will continue through only one animation cycle. (The concept of an animation cycle will be explained later.)
The second parameter in Listing 7 specifies that the single animation cycle will be executed from start to finish over a time period of 20,000 milliseconds (20 seconds). As a result, twenty seconds are required for the white sphere to make one complete revolution around the yellow sphere and return to its original starting position as shown in Figure 4.
Create a RotationInterpolator object
Listing 8 creates a RotationInterpolator object that will cause the objects in the rotationXform group to rotate 360 degrees about the vertical axis (one animation cycle) in the time specified for one cycle by the rotationAlpha object (20 seconds). This satisfies step 3 in Bouvier's recipe shown in Figure 1.
Listing 8. Create a RotationInterpolator object.
RotationInterpolator rotator =
new RotationInterpolator(
rotationAlpha,rotationXform);
|
What is a RotationInterpolator object?
Note that Bouvier's recipe in Figure 1 simply specifies the creation of an interpolator object, not necessarily a RotationInterpolator object. RotationInterpolator is an indirect subclass of the Interpolator class.
Class/subclass hierarchy for the Interpolator class
As of Java 3D version 1.5.0, the class/subclass hierarchy for the Interpolator class includes the seventeen different classes shown in Figure 5.
Figure 5. Class/subclass hierarchy for the Interpolator class.
|
Many different animation possibilities
Presumably, step 3 of Bouvier's recipe could be satisfied using most of the classes shown in Figure 5 to instantiate an object. (If I counted correctly, only two of the classes shown in Figure 5 are abstract.) The large number of non-abstract classes and the names of the classes in Figure 5 indicate that many different animation possibilities are available using an Interpolator object instantiated from one of the subclasses of the Interpolator class.
The RotationInterpolator class
For this program and this lesson, we are interested only in the RotationInterpolator class. (I will explore the use of some of the other interpolator classes in a future lesson on advanced animation using the Java 3D API.)
Sun describes the RotationInterpolator class as follows:
"Rotation interpolator behavior. This class defines a behavior that modifies the rotational component of its target TransformGroup by linearly interpolating between a pair of specified angles (using the value generated by the specified Alpha object). The interpolated angle is used to generate a rotation transform about the local Y-axis of this interpolator."
While I can't tell you exactly how this process works behind the scenes, I can tell you how it appears to work from a functional viewpoint.
During each animation cycle, the Alpha object generates a value that increases from a value of 0.0 to a value of 1.0 according to the parameter values used in the construction of the Alpha object.
Get the alpha value at uniform intervals
There is a clock that fires events at uniform intervals. Each time an event is fired, the Interpolator object gets the alpha value (between 0.0 and 1.0) from the Alpha object. My guess is that the Interpolator object calls the value method of the Alpha object which has the following behavior to get the alpha value:
"This method returns a value between 0.0 and 1.0 inclusive, based on the current time and the time-to-alpha parameters established for this alpha..."
Used to establish percentage of completion
The Interpolator object uses each successive alpha value as a fraction or percentage of 1.0 to determine the percentage of completion of one animation cycle that should have transpired at that point in time. That information is used to transform the initial state of the universe into a new state that reflects the appropriate percentage completion of the animation cycle. This new state is rendered on the screen.
In order to create complex Java 3D animations, you need to understand the detailed behavior of an Alpha object for the different combinations and values of parameters passed to the constructor. I will explain that detailed behavior in a future lesson
Tricking the viewer
The series of renderings showing successive intermediate states of the universe tricks the viewer into seeing the change in position, orientation, color, transparency, etc., as a (hopefully) smooth transition from the initial state to the final state.
The visual quality of the animation
The extent to which the transition appears to be smooth will depend on many factors, including the computational and rendering speed of the computer. For example, on my relatively slow laptop computer, the transition produced by this program has a couple of obvious pauses causing the animation quality to be less than ideal.
One of two RotationInterpolator constructors
The RotationInterpolator class provides two overloaded constructors. Listing 8 uses the simpler of the two, which is described in Figure 6.
Figure 6. One of two RotationInterpolator constructors.
RotationInterpolatorpublic RotationInterpolator(Alpha alpha,
TransformGroup target)
|
An animation cycle
Finally we have the information that we need to understand what constitutes an "animation cycle." When this interpolator is used to animate a target transform group of objects, the target will be rotated from a minimum angle of 0.0 degrees to a maximum angle of 2*pi radians (360 degrees or one revolution). This is one animation cycle as produced by this interpolator.
(Other Interpolator objects are likely to have different animation cycles. For example, the animation cycle for a ColorInterpolator object is not likely to be based on angles.)
The interpolator and alpha objects work together
With the interpolator and the alpha object working together as described earlier, this one revolution of target rotation will take place, over the elapsed time specified in the construction of the alpha object (20 seconds in this program).
As we learned earlier, the various constructor parameters for the Alpha object determine how this will be accomplished:
For the simple constructor used in this program (see Listing 7) the first parameter specifies the number of repetitions and the second parameter specifies the elapsed execution time for one animation cycle.
For this program (again see Listing 7), the parameters specify that a single animation cycle will be executed over an elapsed time of 20 seconds. This causes the yellow and white spheres shown in Figure 2 to rotate one revolution around the Y-axis over a period of 20 seconds.
Specify the active animation region
Apparently for reasons of computational efficiency, it is necessary to specify a region in 3D space to which the animation behavior will be applied. Presumably, any objects belonging to the target group that fall inside that region will be animated and objects belonging to the target group that fall outside that region will be ignored insofar as animation is concerned.
Listing 9 calls the setSchedulingBounds method on the RotationInterpolator object to establish that region.
Listing 9. Specify the active animation region.
rotator.setSchedulingBounds(boundingSphere); |
The setSchedulingBounds method
The setSchedulingBounds method requires an incoming parameter of type Bounds. The abstract Bounds class has the following three subclasses:
An object of any of these three classes will satisfy the parameter type requirement. This program uses an object of the BoundingSphere class that defines a spherical bounding region, which is defined by a center point and a radius. In fact, this program uses the same BoundingSphere object for this purpose that is also used to specify which objects will be illuminated by the point light source (see Listing 4).
The statement in Listing 9 satisfies step 4 in Bouvier's recipe shown in Figure 1.
Construct the entire BranchGroup object
Listing 10 constructs the entire BranchGroup object by adding objects as children of other objects in the correct hierarchy. This satisfies step 5 in Bouvier's recipe.
Listing 10. Construct the entire BranchGroup object.
//Add the objects to the group that controls
// the animation.
rotationXform.addChild(rotator);
rotationXform.addChild(yellowSph);
rotationXform.addChild(whiteTransformGroup);
//Disable the earlier statement that adds the
// pointLight to the branchGroup and enable the
// following statement to get a very different
// effect
//rotationXform.addChild(pointLight);
//Add the group that will be animated to the main
// branch of the scene graph.
branchGroup.addChild(rotationXform);
//THE CODE THAT IMPLEMENTS THE ANIMATION ENDS HERE
|
Wrap it up
Listing 10 also signals the end of the code that has anything to do specifically with animation in this program.
The remaining program code is shown in Listing 11.
Listing 11. Wrap it up.
//Specify the apparent location of the viewer's eye.
simpleUniverse.getViewingPlatform().
setNominalViewingTransform();
//Populate the universe by adding the branch group
// that contains the objects.
simpleUniverse.addBranchGraph(branchGroup);
//Do the normal GUI stuff.
setTitle("Copyright 2007, R.G.Baldwin");
setBounds(0,0,235,235);
setVisible(true);
//This listener is used to terminate the program
// when the user clicks the X-button on the Frame.
addWindowListener(
new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}//end windowClosing
}//end new WindowAdapter
);//end addWindowListener
}//end constructor
//--------------------------------------------------//
}//end inner class TheScene
}//end class Java3D005
|
The code in Listing 11 is the same as the code that I explained in the previous lesson. I won't repeat that explanation here.
I encourage you to copy the code from Listing 12 into your text editor, compile it, and execute it. Experiment with it, making changes, and observing the results of your changes.
Don't forget that Listing 12 contains two versions of the same program. As written, the program should produce the animated screen output shown by the top two images in Figure 2. For this version, the light source maintains its original position while the yellow and white spheres rotate about the vertical axis in 3D space.
If you make the changes indicated by the comments in the program, it should produce the animated screen output shown by the bottom two images in Figure 2. For this version, the light source also rotates about the vertical axis in 3D space in synchronism with the rotation of the yellow sphere.
In both versions, the green sphere is unaffected by the animation and maintains its original position. Of course, the shadows on that sphere change as the light source rotates around the vertical axis in the second version of the program.
Remember, you will need to download and install the Java 3D API plus either Microsoft DirectX or OpenGL to compile and execute these programs. See Downloads for links to the web sites from which this material can be downloaded.
In this lesson, I taught you how to use the RotationInterpolator and Alpha classes of the Java 3D API, along with other necessary classes, to write a simple animation program. I also explained the rationale by which those classes are used to write animation programs.
In the next lesson, I will explain the detailed behavior of an Alpha time-base object. The topics for future lessons include interactive Java 3D programs, advanced animation, and surfaces.
Listing 12. Program listing for the program named Java3D005.
/*File Java3D005.java
Copyright 2007, R.G.Baldwin
The purpose of this program is to create a simple
animation program that will animate the virtual universe
that was developed in Java3D004.
The location of the white sphere was modified relative to
the original virtual universe. The modification causes
the white sphere to be in the horizontal plane. This
causes the white sphere to later be animated so as to
appear to be in a synchronous orbit around the yellow
sphere.
The universe was animated by causing the yellow sphere to
slowly rotate on its vertical axis through one complete
revolution. The yellow sphere carries the small white
sphere along with it just as though the white sphere is
orbiting the yellow sphee in a synchronous circular orbit.
The small green sphere does not rotate with the yellow
sphere, but maintains its original position.
In addition, comments are provided to show how to cause
the light source to also rotate around the vertical axis
in 3D space in synchronism with the rotation of the yellow
sphere. This produces a very different effect causing
shadows to move across the spheres.
Tested using Java SE 6, and Java 3D 1.5.0 running under
Windows XP.
*********************************************************/
import com.sun.j3d.utils.universe.SimpleUniverse;
import com.sun.j3d.utils.geometry.Sphere;
import com.sun.j3d.utils.geometry.Primitive;
import javax.media.j3d.Appearance;
import javax.media.j3d.Material;
import javax.media.j3d.PointLight;
import javax.media.j3d.BranchGroup;
import javax.media.j3d.Canvas3D;
import javax.media.j3d.Transform3D;
import javax.media.j3d.TransformGroup;
import javax.media.j3d.BoundingSphere;
import javax.media.j3d.Alpha;
import javax.media.j3d.RotationInterpolator;
import javax.vecmath.Vector3f;
import javax.vecmath.Point3f;
import javax.vecmath.Point3d;
import javax.vecmath.Color3f;
import java.awt.Frame;
import java.awt.Label;
import java.awt.BorderLayout;
import java.awt.event.WindowAdapter;
import java.awt.event.WindowEvent;
//This is the top-level driver class for this program.
// This program could be written without the use of this
// driver class. However, I decided to keep it intact
// for future expansions that require a user input GUI.
public class Java3D005 extends Frame{
public static void main(String[] args){
Java3D005 thisObj = new Java3D005();
}//end main
//----------------------------------------------------//
public Java3D005(){//constructor
setTitle("Copyright 2007, R.G.Baldwin");
add(new Label("You can build a GUI here."));
setBounds(236,0,235,75);
setVisible(true);
//Instantiate the object in which the Java 3D
// universe will be displayed.
TheScene theScene = new TheScene();
//This window listener is used to terminate the
// program when the user clicks the X button.
addWindowListener(
new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}//end windowClosing
}//end new WindowAdapter
);//end addWindowListener
}//end constructor
//----------------------------------------------------//
//This is an inner class, from which the object in which
// the Java 3D universe will be displayed is
// instantiated.
class TheScene extends Frame{
TheScene(){//constructor
//Create a Canvas3D object to be used for rendering
// the Java 3D universe. Place it in the CENTER of
// the Frame.
Canvas3D canvas3D = new Canvas3D(
SimpleUniverse.getPreferredConfiguration());
add(BorderLayout.CENTER,canvas3D);
//Construct the objects that will be displayed in
// the scene
//Create and set properties for the large yellow
// sphere.
//Begin by describing the appearance of the surface
// of the large sphere. Make the color of the large
// sphere yellow.
Material yellowSphMaterial = new Material();
yellowSphMaterial.setDiffuseColor(1.0f,1.0f,0.0f);
Appearance yellowSphAppearance = new Appearance();
yellowSphAppearance.setMaterial(yellowSphMaterial);
//Now instantiate the large yellow sphere with 9
// divisions. Set the radius to 0.5. The reason for
// setting GENERATE_NORMALS is unclear at this time.
Sphere yellowSph = new Sphere(
0.5f,
Primitive.GENERATE_NORMALS,
9,
yellowSphAppearance);
//Now create a small white sphere with 50 divisions.
Material whiteSphMaterial = new Material();
whiteSphMaterial.setDiffuseColor(1.0f,1.0f,1.0f);
Appearance whiteSphAppearance = new Appearance();
whiteSphAppearance.setMaterial(whiteSphMaterial);
Sphere whiteSph = new Sphere(
0.10f,
Primitive.GENERATE_NORMALS,
50,
whiteSphAppearance);
//Translate the location of the white sphere to make
// it closer to the viewer than the yellow sphere at
// the origin.
Transform3D whiteTransform = new Transform3D();
//The following is a modification to the original
// virtual universe that causes the white sphere to
// be in the horizontal plane. This causes the
// white sphere to later be animated so as to appear
// to be in a synchronous orbit around the yellow
// sphere.
whiteTransform.setTranslation(
new Vector3f(-0.5f,-0.0f,0.5f));
TransformGroup whiteTransformGroup =
new TransformGroup();
whiteTransformGroup.setTransform(whiteTransform);
whiteTransformGroup.addChild(whiteSph);
//Now create a small green sphere located up to the
// right and behind the yellow sphere.
Material greenSphMaterial = new Material();
greenSphMaterial.setDiffuseColor(0.0f,1.0f,0.0f);
Appearance greenSphAppearance = new Appearance();
greenSphAppearance.setMaterial(greenSphMaterial);
Sphere greenSph = new Sphere(
0.10f,
Primitive.GENERATE_NORMALS,
50,
greenSphAppearance);
Transform3D greenTransform = new Transform3D();
greenTransform.setTranslation(
new Vector3f(0.5f,0.5f,-0.5f));
TransformGroup greenTransformGroup =
new TransformGroup();
greenTransformGroup.setTransform(greenTransform);
greenTransformGroup.addChild(greenSph);
//Add a white point light, in front of, to the
// right of, and above the yellow sphere.
Color3f pointLightColor =
new Color3f(1.0f,1.0f,1.0f);
Point3f pointLightPosition =
new Point3f(1.0f,1.0f,2.0f);
Point3f pointLightAttenuation =
new Point3f(1.0f,0.0f,0.0f);
PointLight pointLight = new PointLight(
pointLightColor,
pointLightPosition,
pointLightAttenuation);
//Create a BoundingSphere object and use it to
// determine which objects to light. Also use it
// later to determine which objects to animate.
BoundingSphere boundingSphere =
new BoundingSphere(new Point3d(0.0,0.0,0.0),1.0);
pointLight.setInfluencingBounds(boundingSphere);
//Create an empty Java 3D universe and associate it
// with the Canvas3D object in the CENTER of the
// frame.
SimpleUniverse simpleUniverse =
new SimpleUniverse(canvas3D);
//Create and populate a BranchGroup object.
BranchGroup branchGroup = new BranchGroup();
//Add objects to the branchGroup. Note that the
// yellow and white spheres are no longer added to
// the branchGroup object, but rather are later
// added to a group that causes them to be animated.
branchGroup.addChild(greenTransformGroup);
//If you disable the following statement and enable
// a statement later that adds the pointLight to
// the rotationXform, you will see a very different
// effect. This will cause the light source to
// rotate with the yellow sphere causing the shadows
// to move across the spheres.
branchGroup.addChild(pointLight);
//THE CODE THAT IMPLEMENTS THE ANIMATION BEGINS HERE
//Create a transform group that will be populated
// with the yellow sphere and the white sphere
// transform group. Objects or groups of objects
// belonging to this group will be animated.
TransformGroup rotationXform = new TransformGroup();
rotationXform.setCapability(
TransformGroup.ALLOW_TRANSFORM_WRITE);
//Create an Alpha object that will be used to cause
// the objects in the rotationXform group to
// complete one animation cycle in 20 seconds.
Alpha rotationAlpha = new Alpha(1,20000);
//Create an Interpolator object that will cause the
// objects in the rotationXform group to rotate 360
// degrees about the vertical axis in the time
// specified for one cycle by the rotationAlpha
// object.
RotationInterpolator rotator =
new RotationInterpolator(
rotationAlpha,rotationXform);
//Specify a region in 3D space containing the
// objects or groups of objects that will be
// animated.
rotator.setSchedulingBounds(boundingSphere);
//Add the objects to the group that controls
// the animation.
rotationXform.addChild(rotator);
rotationXform.addChild(yellowSph);
rotationXform.addChild(whiteTransformGroup);
//Disable the earlier statement that adds the
// pointLight to the branchGroup and enable the
// following statement to get a very different
// effect
//rotationXform.addChild(pointLight);
//Add the group that will be animated to the main
// branch of the scene graph.
branchGroup.addChild(rotationXform);
//THE CODE THAT IMPLEMENTS THE ANIMATION ENDS HERE
//Specify the apparent location of the viewer's eye.
simpleUniverse.getViewingPlatform().
setNominalViewingTransform();
//Populate the universe by adding the branch group
// that contains the objects.
simpleUniverse.addBranchGraph(branchGroup);
//Do the normal GUI stuff.
setTitle("Copyright 2007, R.G.Baldwin");
setBounds(0,0,235,235);
setVisible(true);
//This listener is used to terminate the program
// when the user clicks the X-button on the Frame.
addWindowListener(
new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}//end windowClosing
}//end new WindowAdapter
);//end addWindowListener
}//end constructor
//--------------------------------------------------//
}//end inner class TheScene
}//end class Java3D005
|
Copyright 2007, Richard G. Baldwin. Reproduction in whole or in part in any form or medium without express written permission from Richard Baldwin is prohibited.
Richard has participated in numerous consulting projects and he frequently provides onsite training at the high-tech companies located in and around Austin, Texas. He is the author of Baldwin's Programming Tutorials, which have gained a worldwide following among experienced and aspiring programmers. He has also published articles in JavaPro magazine.
In addition to his programming expertise, Richard has many years of practical experience in Digital Signal Processing (DSP). His first job after he earned his Bachelor's degree was doing DSP in the Seismic Research Department of Texas Instruments. (TI is still a world leader in DSP.) In the following years, he applied his programming and DSP expertise to other interesting areas including sonar and underwater acoustics.
Richard holds an MSEE degree from Southern Methodist University and has many years of experience in the application of computer technology to real-world problems.
Keywords
java "java 3D" SimpleUniverse ColorCube BranchGroup canvas
setNominalViewingTransform getPreferredConfiguration SimpleUniverse Sphere
Primitive Appearance Material PointLight BranchGroup Canvas3D Transform3D
TransformGroup BoundingSphere Vector3f Point3f Point3d Color3f
ALLOW_TRANSFORM_WRITE Alpha Interpolator RotationInterpolator
-end-