| << Chapter < Page | Chapter >> Page > |
The hysteresis curves for a ferromagnetic material are more complex than those for diamagnets or paramagnets. Below diagram shows the main features of such a curve for a simple ferromagnet.
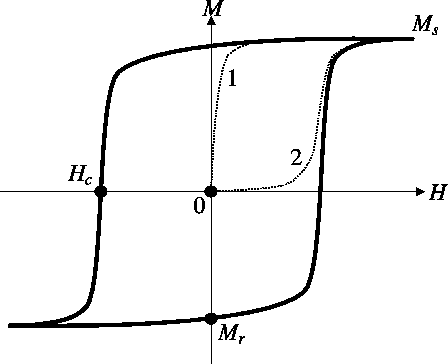
In the virgin material (point 0) there is no magnetization. The process of magnetization, leading from point 0 to saturation at M = M s , is outlined below. Although the material is ordered ferromagnetically it consists of a number of ordered domains arranged randomly giving no net magnetization. This is shown in below (a) with two domains whose individual saturation moments, M s , lie antiparallel to each other.
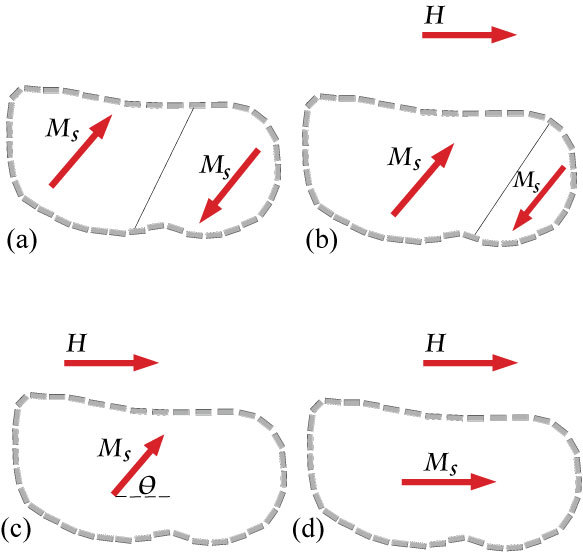
As the magnetic field, H , is applied, (b), those domains which are more energetically favorable increase in size at the expense of those whose moment lies more antiparallel to H . There is now a net magnetization; M . Eventually a field is reached where all of the material is a single domain with a moment aligned parallel, or close to parallel, with H . The magnetization is now M = M s CosΘ where Θ is the angle between M s along the easy magnetic axis and H . Finally M s is rotated parallel to H and the ferromagnet is saturated with a magnetization M = M s .
The process of domain wall motion affects the shape of the virgin curve. There are two qualitatively different modes of behavior known as nucleation and pinning, shown in [link] as curves 1 and 2, respectively.
In a nucleation-type magnet saturation is reached quickly at a field much lower than the coercive field. This shows that the domain walls are easily moved and are not pinned significantly. Once the domain structure has been removed the formation of reversed domains becomes difficult, giving high coercivity. In a pinning-type magnet fields close to the coercive field are necessary to reach saturation magnetization. Here the domain walls are substantially pinned and this mechanism also gives high coercivity.
As the applied field is reduced to 0 after the sample has reached saturation the sample can still possess a remnant magnetization, M r . The magnitude of this remnant magnetization is a product of the saturation magnetization, the number and orientation of easy axes and the type of anisotropy symmetry. If the axis of anisotropy or magnetic easy axis is perfectly aligned with the field then M r = M s , and if perpendicular M r = 0 .
At saturation the angular distribution of domain magnetizations is closely aligned to H . As the field is removed they turn to the nearest easy magnetic axis. In a cubic crystal with a positive anisotropy constant, K 1 , the easy directions are<100>. At remnance the domain magnetizations will lie along one of the three<100>directions. The maximum deviation from H occurs when H is along the<111>axis, giving a cone of distribution of 55 o around the axis. Averaging the saturation magnetization over this angle gives a remnant magnetization of 0.832 M s .

Notification Switch
Would you like to follow the 'Nanomaterials and nanotechnology' conversation and receive update notifications?