| << Chapter < Page | Chapter >> Page > |
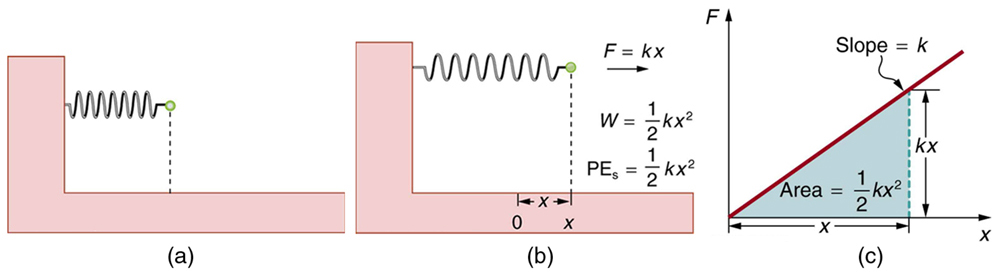
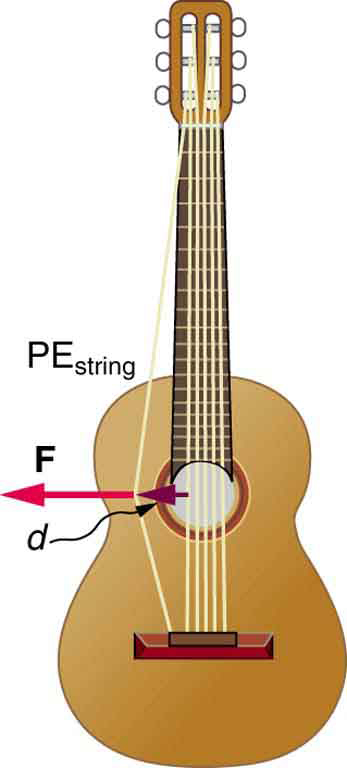
The equation has general validity beyond the special case for which it was derived. Potential energy can be stored in any elastic medium by deforming it. Indeed, the general definition of potential energy is energy due to position, shape, or configuration. For shape or position deformations, stored energy is , where is the force constant of the particular system and is its deformation. Another example is seen in [link] for a guitar string.
Let us now consider what form the work-energy theorem takes when only conservative forces are involved. This will lead us to the conservation of energy principle. The work-energy theorem states that the net work done by all forces acting on a system equals its change in kinetic energy. In equation form, this is
If only conservative forces act, then
where is the total work done by all conservative forces. Thus,
Now, if the conservative force, such as the gravitational force or a spring force, does work, the system loses potential energy. That is, . Therefore,
or
This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces. That is,
where i and f denote initial and final values. This equation is a form of the work-energy theorem for conservative forces; it is known as the conservation of mechanical energy principle. Remember that this applies to the extent that all the forces are conservative, so that friction is negligible. The total kinetic plus potential energy of a system is defined to be its mechanical energy , . In a system that experiences only conservative forces, there is a potential energy associated with each force, and the energy only changes form between and the various types of , with the total energy remaining constant.
The internal energy of a system is the sum of the kinetic energies of all of its elements, plus the potential energy due to all of the interactions due to conservative forces between all of the elements.
Consider a wind-up toy, such as a car. It uses a spring system to store energy. The amount of energy stored depends only on how many times it is wound, not how quickly or slowly the winding happens. Similarly, a dart gun using compressed air stores energy in its internal structure. In this case, the energy stored inside depends only on how many times it is pumped, not how quickly or slowly the pumping is done. The total energy put into the system, whether through winding or pumping, is equal to the total energy conserved in the system (minus any energy loss in the system due to interactions between its parts, such as air leaks in the dart gun). Since the internal energy of the system is conserved, you can calculate the amount of stored energy by measuring the kinetic energy of the system (the moving car or dart) when the potential energy is released.

Notification Switch
Would you like to follow the 'Work and energy' conversation and receive update notifications?